L1/L2 正则化与高斯先验/对数先验的 MAP 贝叶斯推断的关系
1. MAP 贝叶斯推断
贝叶斯推断和极大似然的用处一样,都是求生成训练数据的参数 θ \theta θ ,但是极大似然估计是基于频率派的思想,而贝叶斯推断是基于贝叶斯派的思想。
MAP(Maximum A Posteriori, MAP)最大后验估计点估计。
θ M A P = a r g m a x θ p ( θ ∣ x ) = a r g m a x θ log p ( x ∣ θ ) + log p ( θ ) \theta_{MAP} = \underset{\theta}{argmax} p(\theta|x)=\underset{\theta}{argmax} \log p(x|\theta)+\log p(\theta) θMAP=θargmaxp(θ∣x)=θargmaxlogp(x∣θ)+logp(θ)
p ( θ ) p(\theta) p(θ) 是先验分布,例如考虑具有高斯先验权重的线性回归模型。如果先验是 N ( θ ; 0 , 1 λ I 2 ) N(\theta;0, \frac{1}{\lambda }I^2) N(θ;0,λ1I2) ,那么 log p ( θ ) = − λ w T w 2 I 2 + C \log p(\theta)=-\frac{\lambda w^T w}{2I^2}+ C logp(θ)=−2I2λwTw+C, C C C 是常数,转化为求极小问题可以发现其对应着 L 2 L2 L2 权重衰减。因此具有高斯先验权重的 MAP 贝叶斯推断对应着 L 2 L2 L2 权重衰减。
2. L2正则化
关于 L 2 L2 L2 正则化的形式不再赘述,下面只是从代数角度分析一些 L 2 L2 L2 原理。
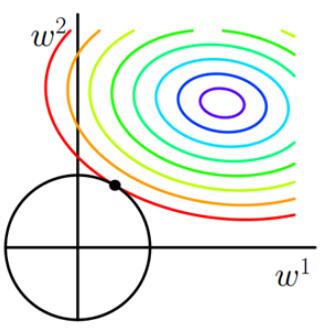
对于不加正则化的目标函数在最优点 w ∗ w^* w∗ 处二阶泰勒展开为 J ( w ) = J ( w ∗ ) + 1 2 ( w − w ∗ ) T H ( w − w ∗ ) J(w)=J(w^*)+\frac{1}{2}(w-w^*)^TH(w-w^*) J(w)=J(w∗)+21(w−w∗)TH(w−w∗) 其中 H H H 是 w ∗ w^* w∗ 处的 Hessian 矩阵,一阶项由于等于 0 省略。因为 w ∗ w^* w∗ 最优,所以可以知道 H H H 是半正定的。
然后考虑加上 L 2 L2 L2 正则的目标函数(在 w ∗ w^* w∗ 附近) L ( w ) = J ( w ) + λ w T w = J ( w ∗ ) + 1 2 ( w − w ∗ ) T H ( w − w ∗ ) + λ w T w L(w) = J(w)+\lambda w^Tw=J(w^*)+\frac{1}{2}(w-w^*)^TH(w-w^*)+\lambda w^Tw L(w)=J(w)+λwTw=J(w∗)+21(w−w∗)TH(w−w∗)+λwTw 。
对其求一阶导令其等于 0 有
λ w + H ( w − w ∗ ) = 0 \lambda w + H(w-w^*)=0 λw+H(w−w∗)=0
得到最优解 w ^ = ( H + λ I ) − 1 H w ∗ \hat{w}=(H+\lambda I)^{-1}Hw^* w^=(H+λI)−1Hw∗ ,比较未添加正则项之前的最优解 w ∗ w^* w∗ 和 w ^ \hat{w} w^ 之间的区别,就能明白 L 2 L2 L2 正则做了一件什么样的事情。因为 H H H 半正定,故存在正交矩阵 Q Q Q 使得 H = Q Λ Q T H= Q\Lambda Q^T H=QΛQT ,代入
w ^ = ( Q Λ Q T + λ I ) − 1 Q Λ Q T w ∗ = [ Q ( Λ + λ I ) Q ] − 1 Q Λ Q T w ∗ = Q ( Λ + λ I ) − 1 Λ Q T w ∗ \hat{w}=(Q\Lambda Q^T+\lambda I)^{-1}Q\Lambda Q^Tw^*=[Q(\Lambda + \lambda I) Q]^{-1}Q\Lambda Q^Tw^*=Q(\Lambda + \lambda I)^{-1}\Lambda Q^T w^* w^=(QΛQT+λI)−1QΛQTw∗=[Q(Λ+λI)Q]−1QΛQTw∗=Q(Λ+λI)−1ΛQTw∗
可以看出来权重衰减的效果是针对 H H H 的特征向量所定义的轴缩放 w ∗ w^* w∗ 。具体来说,我们根据 α i α i + λ ( α i 为 H 的 第 i 个 特 征 值 ) \frac{\alpha_i}{\alpha_i+\lambda}(\alpha_i 为 H 的第i个特征值) αi+λαi(αi为H的第i个特征值) 因子缩放与 H H H 第 i i i 个特征向量对齐的 w ∗ w^* w∗ 的分量,当 α i > > λ \alpha_i >> \lambda αi>>λ 时, w i w_i wi 受的影响较小,当 α i < < λ \alpha_i << \lambda αi<<λ 时, w i w_i wi 会收缩到几乎为 0 。
3. L1 正则化
L 1 L1 L1 正则化被定义为 Ω ( θ ) = ∣ ∣ w ∣ ∣ 1 = ∑ i ∣ w i ∣ \Omega(\theta)=||w||_1=\sum_{i}|w_i| Ω(θ)=∣∣w∣∣1=∑i∣wi∣ ,即各个参数的绝对值之和。和上面的分析类似,正则化的目标函数 J ^ ( w ; X , y ) = λ ∣ ∣ w ∣ ∣ 1 + J ( w ; X , y ) \hat{J}(w;X, y)=\lambda ||w||_1 + J(w;X, y) J^(w;X,y)=λ∣∣w∣∣1+J(w;X,y) ,其对应的次梯度为
▽ w J ^ ( w ; X , y ) = λ s i g n ( w ) + ▽ w J ( w ; X , y ) \bigtriangledown_w\hat{J}(w;X, y)=\lambda sign(w) + \bigtriangledown_w J(w;X, y) ▽wJ^(w;X,y)=λsign(w)+▽wJ(w;X,y)
如果没有正则项的最优解为 w ∗ w^* w∗ ,在 w ∗ w^* w∗ 附近的 J J J 的为 J ( w ) = J ( w ∗ ) + 1 2 ( w − w ∗ ) T H ( w − w ∗ ) J(w)=J(w^*)+\frac{1}{2}(w-w^*)^TH(w-w^*) J(w)=J(w∗)+21(w−w∗)TH(w−w∗) , H H H 是在 w ∗ w^* w∗ 的 Hessian 矩阵。为了简化问题,这里假设 H H H 是对角矩阵,则添加上 L 1 L1 L1 正则项的目标函数为
J ^ ( w ; X , y ) = J ( w ∗ ) + ∑ i [ 1 2 H i , i ( w i − w i ∗ ) 2 + λ ∣ w i ∣ ] \hat{J}(w;X, y)=J(w^*)+\sum_{i}[\frac{1}{2}H_{i, i}(w_i-w_i^*)^2+\lambda|w_i|] J^(w;X,y)=J(w∗)+i∑[21Hi,i(wi−wi∗)2+λ∣wi∣]
关于 w i w_i wi 求导求其最小值可得到
w i = s i g n ( w i ∗ ) m a x { ∣ w i ∗ ∣ − λ H i , i , 0 } w_i=sign(w_i^*)max\{|w_i^*|-\frac{\lambda}{H_{i, i}}, 0\} wi=sign(wi∗)max{∣wi∗∣−Hi,iλ,0}
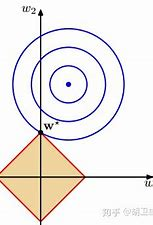
对于每个 i i i ,考虑 w i ∗ > 0 w_i^*>0 wi∗>0 的情形, 会有两种可能结果。
(1) w i ∗ ≤ λ H i , i w_i^*\le \frac{\lambda}{H_{i, i}} wi∗≤Hi,iλ 的情况。正则化后目标中的 w i w_i wi 最优值 w i = 0 w_i=0 wi=0 。 L 1 L1 L1 正则化将 w i w_i wi 推向 0 。
(2) w i ∗ > λ H i , i w_i^*> \frac{\lambda}{H_{i, i}} wi∗>Hi,iλ, L 1 L1 L1 正则化不会将其推至 0,而只是向那个方向移动 λ H i , i \frac{\lambda}{H_{i, i}} Hi,iλ 的距离。
w
i
∗
<
0
w_i^*<0
wi∗<0 的情形与此类似。相比于
L
2
L2
L2 正则,
L
1
L1
L1 正则会产生更为稀疏的解。因此
L
1
L1
L1 可以用来进行 特征选择 。
上面说 L 2 L2 L2 正则是带有高斯先验权重的 MAP,对于 L 1 L1 L1 正则化,是带有各向同性的拉普拉斯先验权重的 MAP 。
log p ( w ) = ∑ i log L a p l a c e ( w i ; 0 , 1 α ) = − α ∣ ∣ w ∣ ∣ 1 + n log α − n log 2 \log p(w)=\sum_{i}\log Laplace(w_i;0, \frac{1}{\alpha})=-\alpha||w||_1+n\log\alpha - n\log 2 logp(w)=i∑logLaplace(wi;0,α1)=−α∣∣w∣∣1+nlogα−nlog2
文章来源:花书p142-p144






















 2602
2602











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








