10 EM（期望最大）算法

hanhan不是很憨憨

于 2023-06-01 17:26:05 发布

阅读量513

点赞数

分类专栏：机器学习-白板推导文章标签：算法机器学习人工智能

本文链接：https://blog.csdn.net/weixin_50737833/article/details/130992708

版权

机器学习-白板推导专栏收录该内容

29 篇文章 0 订阅

订阅专栏

文章目录

10 EM（期望最大）算法

10 EM（期望最大）算法

10.1 背景介绍

概率图模型中，两个核心问题：学习参数、求解后验分布。EM算法就是一种通过MLE求出参数近似解的方法

10.2 EM算法公式

EM算法的具体公式表示为：
$\begin{align} \theta^{(t+1)} & = arg\max_{\theta} \int_Z { \log{P(X, Z| \theta)} \cdot P(Z| X, \theta^{(t)}) } {\rm d}Z \\ & = arg\max_{\theta} E_{Z|X, \theta^{(t)}} [\log P(X, Z| \theta)] \end{align}$
其中上标中的 $t$ 和 $t + 1$ 表示第 $t$ 、 $t + 1$ 次迭代的参数结果，且参数满足： ${\lbrace x_i \rbrace}_{i=1}^N$ ， ${\lbrace z_i \rbrace}_{i=1}^N$ ，且 $z$ 为离散分布：

$z$	$C_1$	$C_2$	$\dots$	$C_k$
$P (z)$	$p_1$	$p_2$	$\dots$	$p_k$

且EM算法分为E-Step和M-Step：

E-Step——通过 $t$ 时刻的参数得到 $t$ 时刻的期望：
$\theta^{(t)} \rightarrow E_{Z|X, \theta^{(t)}} [\log P(X, Z| \theta)]$
M-Step——将当前的最大期望作为移动方向求 $t + 1$ 时刻的参数：
$\theta^{(t+1)} = arg\max_{\theta} E_{Z|X, \theta^{(t)}} [\log P(X, Z| \theta)]$

10.2.1 EM算法公式收敛性证明

若要用EM算法求解参数的近似解，我们需要证明EM算法公式是收敛的，以保证迭代结果离实际结果越来越近。

若要证明EM算法公式收敛，需要有以下条件：

该算法公式有上确界
每一次的迭代结果递增

证明过程如下：

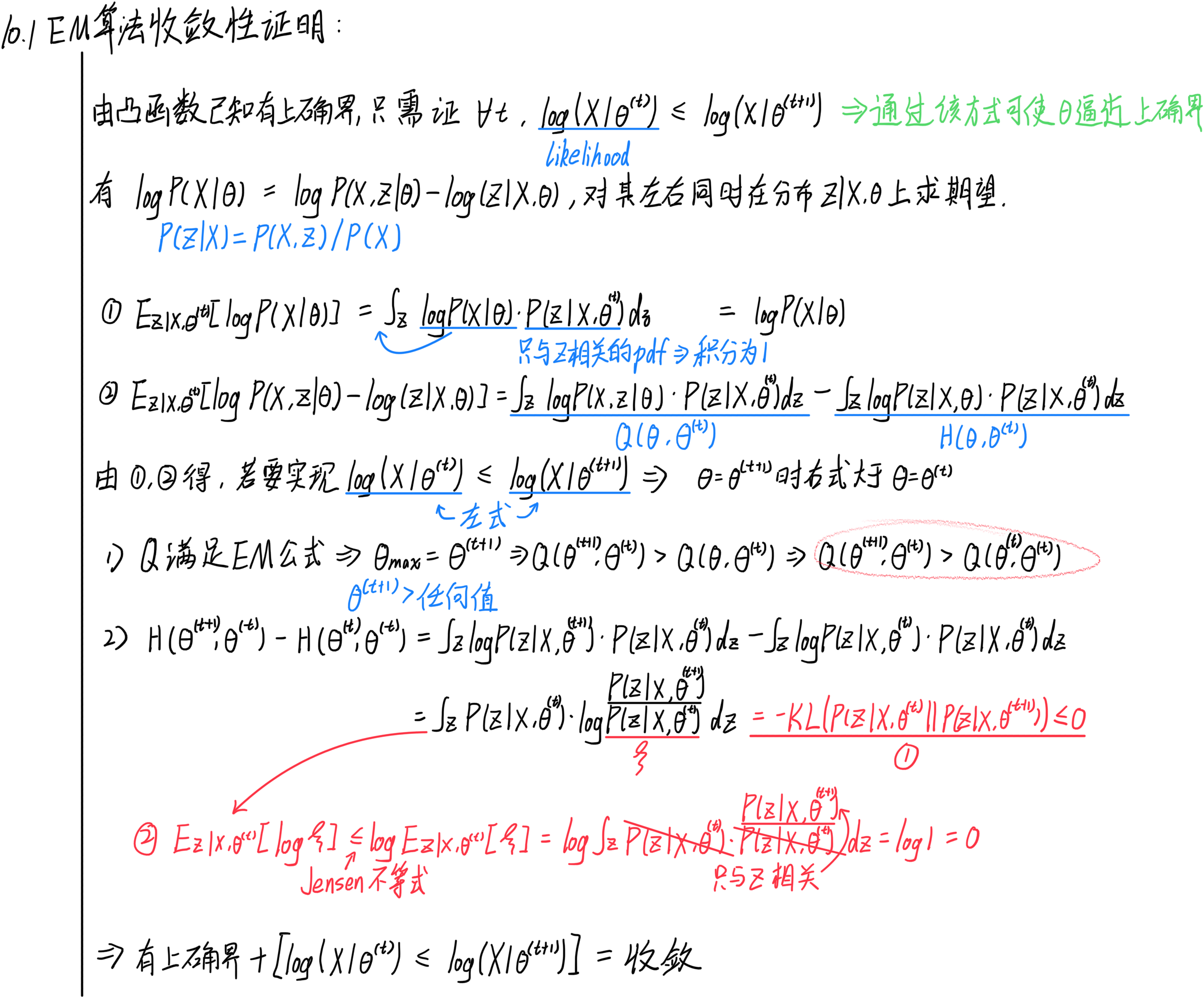
在这里插入图片描述

总而言之：

要证明 $\log(X|\theta^{(t)}) \leq \log(X|\theta^{(t+1)})$ ，可以将其看作 $\log(X|\theta)$ 在 $t + 1$ 时刻比 $t$ 时刻大
上文通过证明 $\log(X|\theta)$ 在 $t + 1$ 时刻减 $t$ 时刻的值 $\geq 0$ ，从而得出收敛性。

10.2.2 EM算法公式导出

下文通过两种方法将EM公式导出，核心思想很简单，就是分解likelihood：

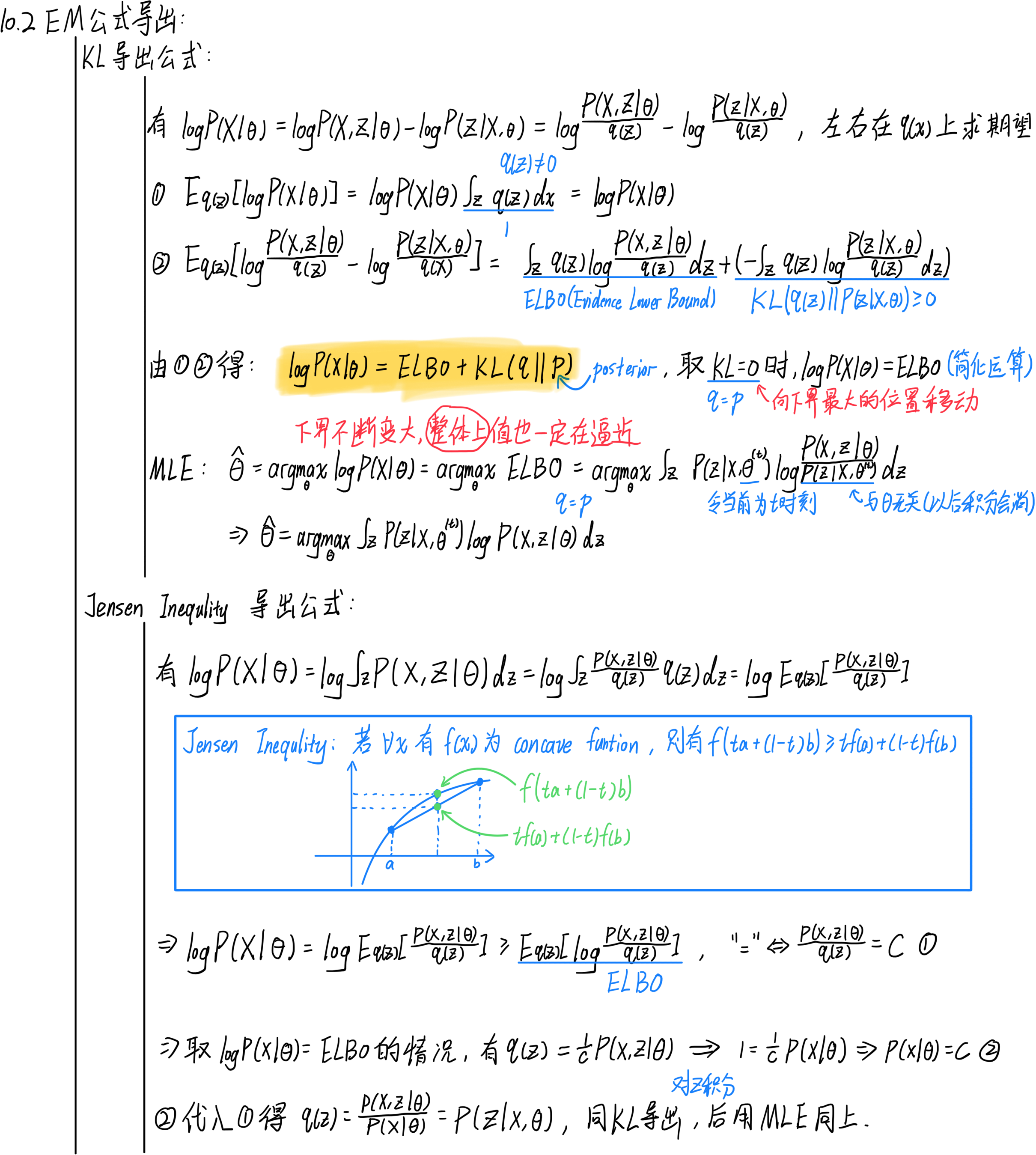
在这里插入图片描述

10.3 广义EM算法

10.3.1 EM有什么作用？

能够解决概率生成模型。条件有 $P(X|\theta)$ ——likelihood、 $X$ 、 $\theta$ 时，EM用于估计 $\hat \theta$
具体通过引入隐变量Z，使得 $\int_Z P(X, Z) {\rm d}Z$ ，然后用MLE求解

10.3.2 为什么要引入广义EM？

引入广义EM必然是因为狭义的EM有问题，狭义的EM可以写为：
$\begin{cases} E-Step: & {\hat q} = P(Z|X, \theta) \impliedby KL = 0 \\ M-Step: & \theta^{(t+1)} = arg\max_{\theta} E_{Z|X, \theta^{(t)}} [\log P(X, Z| \theta)] \end{cases}$
从上面可以看出来我们引入了一个条件： $K L = 0$ ，这个条件并不是很好用：

若非模型非常简单， ${\hat q} = P(Z|X, \theta)$ 实际上很难求解
所以 $\hat q$ 这个参数也需要通过别的方法求出近似解

10.3.3 广义EM公式导出

我们将EM公式重新拆分到优化前的状态：
$\log P(X|\theta) = {\mathcal L}(q, \theta) + KL(q||p), \quad {\mathcal L}(q, \theta) = ELBO$

$\begin{cases} ELBO = E_{q(Z)} [\log \frac{P(X, Z|\theta)}{q(Z)}] \\ KL(q || p) = \int q(Z) \cdot \log \frac{q(Z)}{P(Z|X, \theta)} {\rm d}Z \end{cases}$

所以可以将计算在这里添加一步：

在 $\log P(X|\theta) = {\mathcal L}(q, \theta) + KL(q||p)$ 时固定 $\theta$ （表示在同一个 $\theta$ 下），此时 $\log P(X|\theta)$ 为定值，得到：
${\hat q} = arg\min_q KL(q||p) = arg\max {\mathcal L}(q, \theta)$
求出了 ${\hat q}$ 后，固定 ${\hat q}$ ， $\log P(X|\theta)$ 依旧为定值，求：
${\hat \theta} = arg\max_{\theta} {\mathcal L}({\hat q}, \theta)$

于是就得到了广义EM的E-Step和M-Step：
$\begin{cases} E-Step: & q^{(t+1)} = arg\max_q {\mathcal L}(q, \theta^{(t)}) \\ M-Step: & \theta^{(t+1)} = arg\max_{\theta} {\mathcal L}(q^{(t+1)}, \theta) \end{cases}$
形式上也可以写成下面这两步（也可以叫做MM算法）：
$\begin{cases} M_1-Step: & q^{(t+1)} = arg\max_q {\mathcal L}(q, \theta^{(t)}) \\ M_2-Step: & \theta^{(t+1)} = arg\max_{\theta} E_{q^{(t+1)}} [\log P(X, Z| \theta)] \end{cases}$

10.3.4 广义EM有什么不同

前后在计算上的差别就是期望的分布产生了变化：
$E_{Z|X, \theta^{(t)}} [\log P(X, Z| \theta)] \implies E_{q^{(t+1)}} [\log P(X, Z| \theta)] = {\mathcal L}(q^{(t+1)}, \theta)$
其实如果我们分解 ${\mathcal L}(q, \theta)$ 可以得到：
${\mathcal L}(q, \theta) = E_{q(Z)} [ \log \frac{P(X,Z|\theta)}{q(Z)} ] = E_{q(Z)} [ \log P(X,Z|\theta) ] - E_{q(Z)} [ \log q(Z) ]$
我们发现广义的EM就是比狭义的EM多减去了一个 $E_{q(Z)} [ \log q(Z) ]$ ，我们发现这就是熵的定义，且熵 $H [q (Z)]$ 与 $\theta$ 无关：
$H[q(Z)] = E_{q(Z)} [ \log q(Z) ]$