目录
1.2. 马尔可夫链 (Markov Chain)又是什么鬼
(一),马尔可夫 (Markov)综述
引例:假设我们观测⼀个⼆值变量,这个⼆值变量表⽰某⼀天是否下⾬。给定这个变量的⼀系列观测,我们希望预测下⼀天是否会下⾬。
- 如果我们将所有的数据都看成独⽴同分布的, 那么我们能够从数据中得到的唯⼀的信息就是⾬天的相对频率;
- 然而,我们知道天⽓经常会呈现出持续若⼲天的趋势。因此,观测到今天是否下⾬对于预测明天是否下⾬会 有极⼤的帮助。
我们可以使用概率的乘积规则来表示观测序列的联合概率分布,形式为
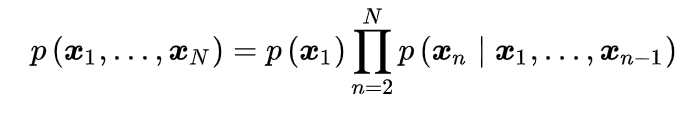
利用马尔科夫性,可以将上式变为⼀阶马尔科夫链(first-order Markov chain):


根据我们在概率图模型中讲的 d-分离 性质,观测 的条件概率分布为
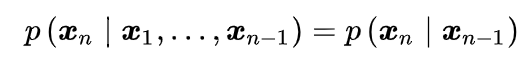
当然了,还可以有⼆阶马尔科夫链,其中特定的观测依赖于前两次观测和的值:


还有M阶马尔可夫链,当然计算代价也很大:

1.1,随机过程是啥玩意儿
讲马尔可夫链不得不提到随机过程,因为它是随机过程课本中的,啊啊。
顾名思义,它其实就是个过程,比如今天下雨,那么明天下不下雨呢?后天下不下雨呢?从今天下雨到明天不下雨再到后天下雨,这就是个过程。那么怎么预测N天后到底下不下雨呢?这其实是可以利用公式进行计算的,随机过程就是这样一个工具,把整个过程进行量化处理,用公式就可以推导出来N天后的天气状况,下雨的概率是多少,不下雨的概率是多少。说白了,随机过程就是一些统计模型,利用这些统计模型可以对自然界的一些事物进行预测和处理,比如天气预报,比如股票,比如市场分析,比如人工智能。它的应用还真是多了去了。
话说回来,还真是佩服能构造出这些统计模型的大牛,简直脑洞大开啊。
1.2. 马尔可夫链 (Markov Chain)又是什么鬼
好了,终于可以来看看马尔可夫链 (Markov Chain)到底是什么了。
它是随机过程中的一种过程,到底是哪一种过程呢?好像一两句话也说不清楚,还是先看个例子吧。
先说说我们村智商为0的王二狗,人傻不拉几的,见人就傻笑,每天中午12点的标配,仨状态:吃,玩,睡。这就是传说中的状态分布。
你想知道他n天后中午12点的状态么?是在吃,还是在玩,还是在睡?这些状态发生的概率分别都是多少? (知道你不想,就假装想知道吧~~学习真的好累~~)
先看个假设,他每个状态的转移都是有概率的,比如今天玩,明天睡的概率是几,今天玩,明天也玩的概率是几几,看图更清楚一点。

这个矩阵就是转移概率矩阵P,并且它是保持不变的,就是说第一天到第二天的转移概率矩阵跟第二天到第三天的转移概率矩阵是一样的。(这个叫时齐,不细说了,有兴趣的同学自行百度)。
有了这个矩阵,再加上已知的第一天的状态分布,就可以计算出第N天的状态分布了。

S1 是4月1号中午12点的的状态分布矩阵 [0.6, 0.2, 0.2],里面的数字分别代表吃的概率,玩的概率,睡的概率。
那么
4月2号的状态分布矩阵 S2 = S1 * P (俩矩阵相乘)。
4月3号的状态分布矩阵 S3 = S2 * P (看见没,跟S1无关,只跟S2有关)。
4月4号的状态分布矩阵 S4 = S3 * P (看见没,跟S1,S2无关,只跟S3有关)。
...
4月n号的状态分布矩阵 Sn = Sn-1 * P (看见没,只跟它前面一个状态Sn-1有关)。
总结:马尔可夫链就是这样一个任性的过程,它将来的状态分布只取决于现在,跟过去无关!
就把下面这幅图想象成是一个马尔可夫链吧。实际上就是一个随机变量随时间按照Markov性进行变化的过程。
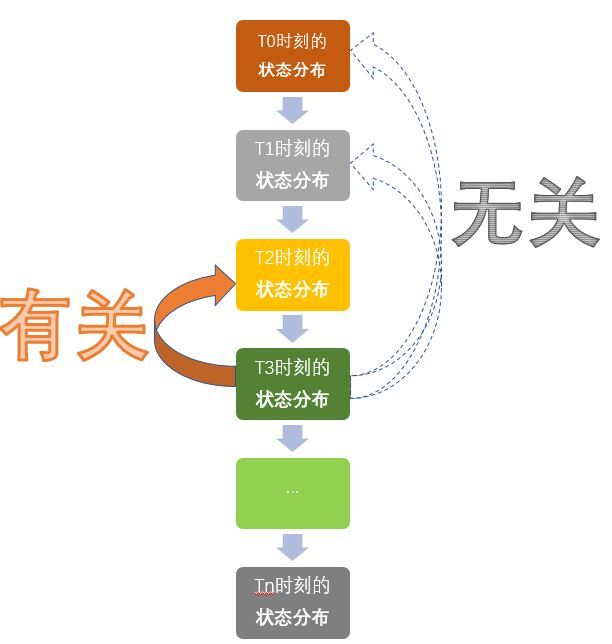
=================================更新============
附:S2 的计算过程 (没兴趣的同学自行略过)
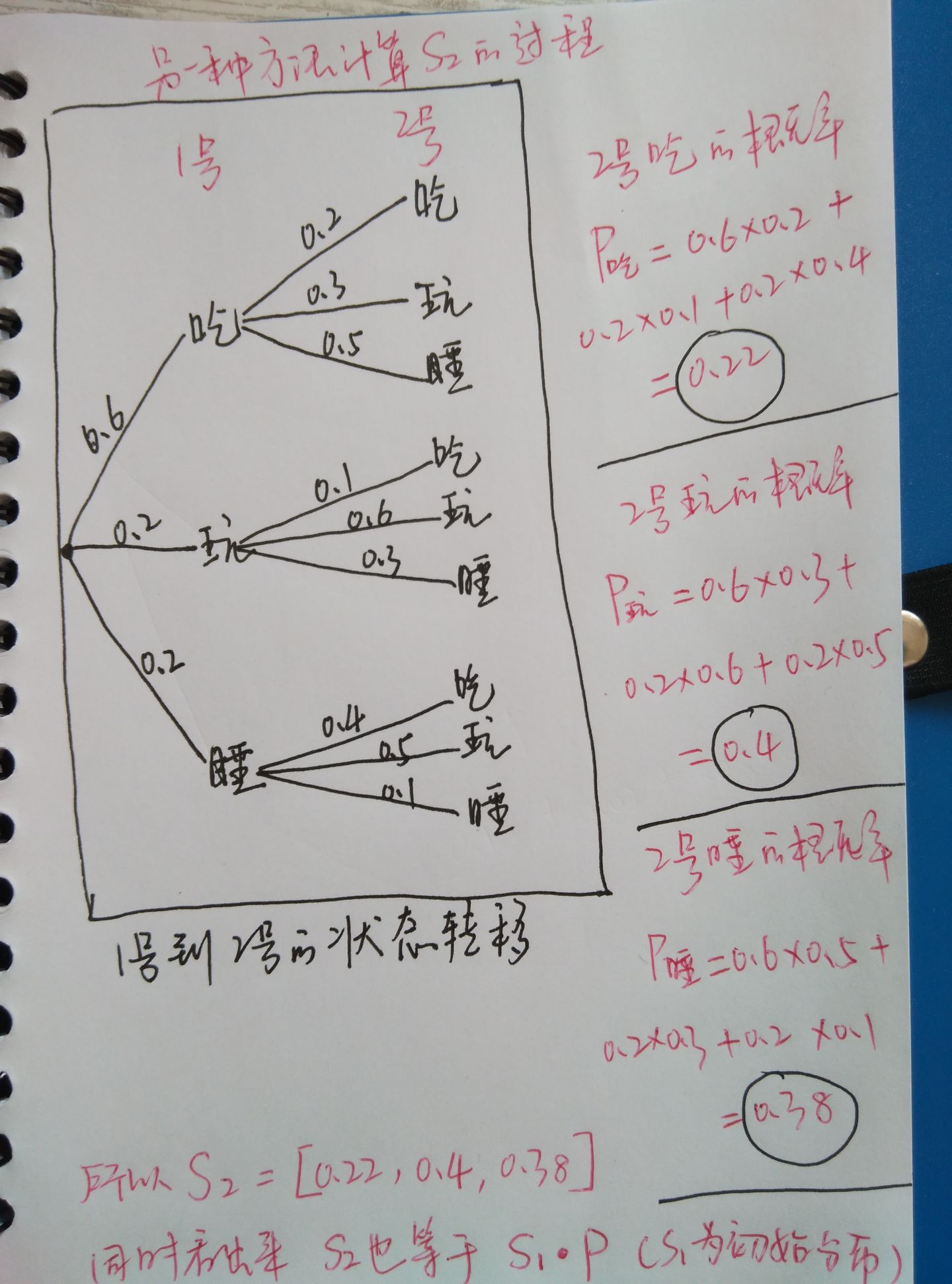
原文链接https://zhuanlan.zhihu.com/p/26453269
1.3一个经典的马尔科夫链实例
用一句话来概括马尔科夫链的话,那就是某一时刻状态转移的概率只依赖于它的前一个状态。举个简单的例子,假如每天的天气是一个状态的话,那个今天是不是晴天只依赖于昨天的天气,而和前天的天气没有任何关系。这么说可能有些不严谨,但是这样做可以大大简化模型的复杂度,因此马尔科夫链在很多时间序列模型中得到广泛的应用,比如循环神经网络RNN,隐式马尔科夫模型HMM等。
假设状态序列为⋯ x t − 2 , x t − 1 , x t , x t + 1 , x t + 2 , ⋯ ⋯ x t − 2 , x t − 1 , x t , x t + 1 , x t + 2 , ⋯ ⋯ x t − 2 , x t − 1 , x t , x t + 1 , x t + 2 , ⋯ ⋯xt−2,xt−1,xt,xt+1,xt+2,⋯⋯xt−2,xt−1,xt,xt+1,xt+2,⋯ \cdots x_{t-2}, x_{t-1}, x_t, x_{t+1}, x_{t+2}, \cdots⋯xt−2,xt−1,xt,xt+1,xt+2,⋯⋯xt−2,xt−1,xt,xt+1,xt+2,⋯⋯xt−2,xt−1,xt,xt+1,xt+2,⋯t0=[0.1,0.2,0.7],然后算之后的状态。
def markov():
init_array = np.array([0.1, 0.2, 0.7])
transfer_matrix = np.array([[0.9, 0.075, 0.025],
[0.15, 0.8, 0.05],
[0.25, 0.25, 0.5]])
restmp = init_array
for i in range(25):
res = np.dot(restmp, transfer_matrix)
print i, "\t", res
restmp = res
markov()结果:
0 [0.295 0.3425 0.3625]
1 [0.4075 0.38675 0.20575]
2 [0.4762 0.3914 0.1324]
3 [0.52039 0.381935 0.097675]
4 [0.55006 0.368996 0.080944]
5 [0.5706394 0.3566873 0.0726733]
6 [0.58524688 0.34631612 0.068437 ]
7 [0.59577886 0.33805566 0.06616548]
8 [0.60345069 0.33166931 0.06487999]
9 [0.60907602 0.32681425 0.06410973]
10 [0.61321799 0.32315953 0.06362248]
11 [0.61627574 0.3204246 0.06329967]
12 [0.61853677 0.31838527 0.06307796]
13 [0.62021037 0.31686797 0.06292166]
14 [0.62144995 0.31574057 0.06280949]
15 [0.62236841 0.31490357 0.06272802]
16 [0.62304911 0.31428249 0.0626684 ]
17 [0.62355367 0.31382178 0.06262455]
18 [0.62392771 0.31348008 0.06259221]
19 [0.624205 0.3132267 0.0625683]
20 [0.62441058 0.31303881 0.06255061]
21 [0.624563 0.31289949 0.06253751]
22 [0.624676 0.3127962 0.0625278]
23 [0.62475978 0.31271961 0.06252061]
24 [0.6248219 0.31266282 0.06251528]
从第18次开始,状态就开始收敛至[ 0.624 , 0.312 , 0.0625 ] [ 0.624 , 0.312 , 0.0625 ] [ 0.624 , 0.312 , 0.0625 ] [0.624,0.312,0.0625][0.624,0.312,0.0625] [0.624, 0.312, 0.0625][0.624,0.312,0.0625][0.624,0.312,0.0625][0.624,0.312,0.0625]P的幂次方有什么有意思的地方?废话不多说,直接上代码。
def matrixpower():
transfer_matrix = np.array([[0.9, 0.075, 0.025],
[0.15, 0.8, 0.05],
[0.25, 0.25, 0.5]])
restmp = transfer_matrix
for i in range(25):
res = np.dot(restmp, transfer_matrix)
print i, "\t", res
restmp = res
matrixpower()结果:
0 [[ 0.8275 0.13375 0.03875]
[ 0.2675 0.66375 0.06875]
[ 0.3875 0.34375 0.26875]]
1 [[ 0.7745 0.17875 0.04675]
[ 0.3575 0.56825 0.07425]
[ 0.4675 0.37125 0.16125]]
2 [[ 0.73555 0.212775 0.051675]
[ 0.42555 0.499975 0.074475]
[ 0.51675 0.372375 0.110875]]
3 [[ 0.70683 0.238305 0.054865]
[ 0.47661 0.450515 0.072875]
[ 0.54865 0.364375 0.086975]]
4 [[ 0.685609 0.2573725 0.0570185]
[ 0.514745 0.4143765 0.0708785]
[ 0.570185 0.3543925 0.0754225]]
5 [[ 0.6699086 0.2715733 0.0585181]
[ 0.5431466 0.3878267 0.0690267]
[ 0.585181 0.3451335 0.0696855]]
6 [[ 0.65828326 0.28213131 0.05958543]
[ 0.56426262 0.36825403 0.06748335]
[ 0.5958543 0.33741675 0.06672895]]
7 [[ 0.64967099 0.28997265 0.06035636]
[ 0.5799453 0.35379376 0.06626094]
[ 0.60356362 0.33130471 0.06513167]]
8 [[ 0.64328888 0.29579253 0.06091859]
[ 0.59158507 0.34309614 0.06531879]
[ 0.60918588 0.32659396 0.06422016]]
9 [[ 0.63855852 0.30011034 0.06133114]
[ 0.60022068 0.33517549 0.06460383]
[ 0.61331143 0.32301915 0.06366943]]
10 [[ 0.635052 0.30331295 0.06163505]
[ 0.60662589 0.3293079 0.06406621]
[ 0.61635051 0.32033103 0.06




 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 273
273

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








