Fourier变换-复数形式-矩形脉冲函数

Universe-hello

已于 2024-04-14 00:44:27 修改

阅读量160

点赞数 1

分类专栏：傅立叶: 级数、积分、变换文章标签：傅立叶分析

于 2024-04-13 23:58:34 首次发布

本文链接：https://blog.csdn.net/weixin_51133173/article/details/137729126

版权

傅立叶: 级数、积分、变换专栏收录该内容

19 篇文章

订阅专栏

文章介绍了使用Python进行Fourier积分的复数形式计算，包括定义函数、计算复数形式的F_w和F_t，并分析了虚部和实部的平均值。内容涉及numpy库的使用以及对信号处理中的频域分析的演示。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

参考：https://ins.sjtu.edu.cn/people/songtingli/resources/slides/MathPhysics/Lecture9.pdf

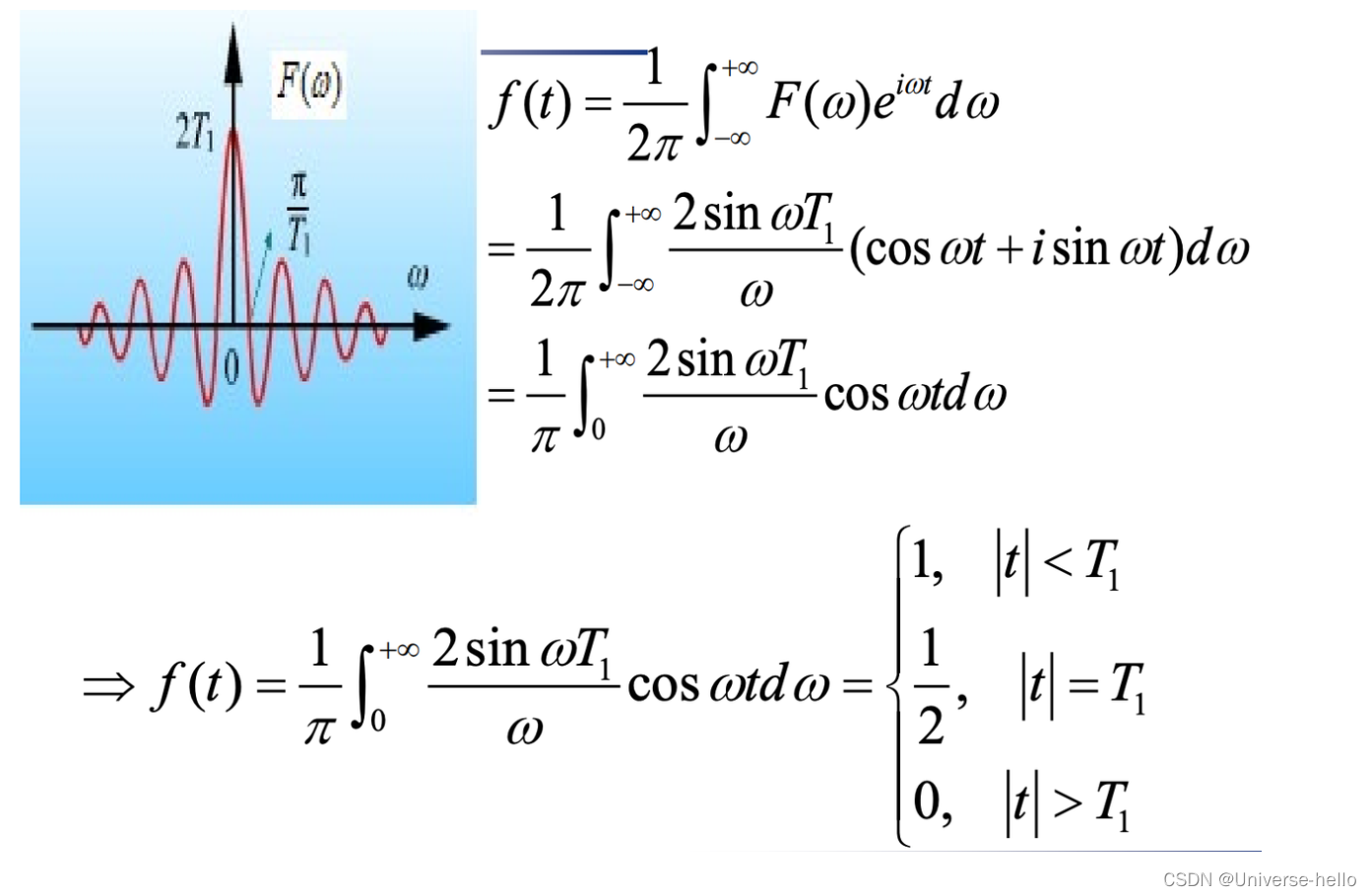
Fourier积分-复数形式

假设T1=1.5，w范围: -30~30

import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm

_, ax = plt.subplots()
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# plt.xlim(-5,5)
# plt.ylim(-1.2,1.2)

start,end = -1.5,1.5
points = 300
T = np.linspace(start,end,points)
f_t = np.empty_like(T)
f_t[:] = 1
plt.scatter(T,f_t,marker='.',s=1,c='b')

# 复数形式
t_start,t_end = start, end
t_segN = 1000
t_points = np.linspace(t_start,t_end,t_segN)
f_t = np.empty_like(t_points)
f_t[:] = 1
F_w = lambda w: np.sum(f_t*np.exp(-1j*w*t_points)*(t_end-t_start)/t_segN)

w_start,w_end = -30,30
w_segN = 800
w_points = np.linspace(w_start,w_end,w_segN)
dw = (w_end-w_start)/w_segN

Fw = [F_w(w) for w in w_points]
print(Fw[0:2])
print('Fw虚部的均值:',np.mean([i.imag for i in Fw]))
print('Fw虚部绝对值的均值:',np.mean([abs(i.imag) for i in Fw]))
print('Fw实部的均值:',np.mean([i.real for i in Fw]))
print('Fw实部绝对值的均值:',np.mean([abs(i.real) for i in Fw]))

Fw_real = [i.real for i in Fw]
Fw_imag = [i.imag for i in Fw]
# plt.scatter(w_points,Fw_real,marker='.',s=1,c='r')

ft = lambda t: sum([F_w(w)*np.exp(1j*w*t)*dw for w in w_points])/(np.pi*2)
F_t = []
for i in tqdm(T):
    F_t.append(ft(i))

print(F_t[0:2])
print('Ft虚部的均值:',np.mean([i.imag for i in F_t]))
Ft_real = [i.real for i in F_t]

plt.scatter(T,Ft_real,marker='.',s=1,c='r')
plt.savefig('f.jpg')

Fourier变换-复数形式

import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm

_, ax = plt.subplots()
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# plt.xlim(-5,5)
# plt.ylim(-1.2,1.2)

start,end = -1.5,1.5
points = 300
T = np.linspace(start,end,points)
f_t = np.empty_like(T)
f_t[:] = 1
# plt.scatter(T,f_t,marker='.',s=1,c='b')

# 复数形式
t_start,t_end = start, end
t_segN = 1000
t_points = np.linspace(t_start,t_end,t_segN)
f_t = np.empty_like(t_points)
f_t[:] = 1
F_w = lambda w: np.sum(f_t*np.exp(-1j*w*t_points)*(t_end-t_start)/t_segN)

w_start,w_end = -30,30
w_segN = 800
w_points = np.linspace(w_start,w_end,w_segN)
dw = (w_end-w_start)/w_segN

Fw = [F_w(w) for w in w_points]
print(Fw[0:2])
print('Fw虚部的均值:',np.mean([i.imag for i in Fw]))
print('Fw虚部绝对值的均值:',np.mean([abs(i.imag) for i in Fw]))
print('Fw实部的均值:',np.mean([i.real for i in Fw]))
print('Fw实部绝对值的均值:',np.mean([abs(i.real) for i in Fw]))

Fw_real = [i.real for i in Fw]
Fw_imag = [i.imag for i in Fw]
plt.scatter(w_points,Fw_real,marker='.',s=1,c='r')

ft = lambda t: sum([F_w(w)*np.exp(1j*w*t)*dw for w in w_points])/(np.pi*2)
F_t = []
for i in tqdm(T):
    F_t.append(ft(i))

print(F_t[0:2])
print('Ft虚部的均值:',np.mean([i.imag for i in F_t]))
Ft_real = [i.real for i in F_t]

# plt.scatter(T,Ft_real,marker='.',s=1,c='r')
plt.savefig('f.jpg')