常用窗函数

最新推荐文章于 2024-05-06 15:38:00 发布

Universe-hello

最新推荐文章于 2024-05-06 15:38:00 发布

阅读量608

点赞数 10

分类专栏：信号与傅立叶文章标签：信号处理傅立叶分析

本文链接：https://blog.csdn.net/weixin_51133173/article/details/137752335

版权

信号与傅立叶专栏收录该内容

15 篇文章

订阅专栏

文章介绍了scipy.signal库中get_window函数，展示了如何使用各种窗函数如Rectangular、Hanning、Hamming和Blackman等的不同形式（对称和周期），以及它们在时域信号处理中的应用，特别是在计算sin(wt)与窗函数的乘积时。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

scipy.signal.get_window()

scipy.signal.get_window()

def get_window(window, Nx, fftbins=True):
    """
    Return a window of a given length and type.

    Parameters
    ----------
    window : string, float, or tuple
        The type of window to create. See below for more details.
    Nx : int
        The number of samples in the window.
    fftbins : bool, optional
        If True (default), create a "periodic周期" window, ready to use with
        `ifftshift` and be multiplied by the result of an FFT (see also
        :func:`~scipy.fft.fftfreq`).
        If False, create a "symmetric对称" window, for use in filter design.

    Returns
    -------
    get_window : ndarray
        Returns a window of length `Nx` and type `window`

    Notes
    -----
    Window types:

    - `~scipy.signal.windows.boxcar`
    - `~scipy.signal.windows.triang`
    - `~scipy.signal.windows.blackman`
    - `~scipy.signal.windows.hamming`
    - `~scipy.signal.windows.hann`
    - `~scipy.signal.windows.bartlett`
    - `~scipy.signal.windows.flattop`
    - `~scipy.signal.windows.parzen`
    - `~scipy.signal.windows.bohman`
    - `~scipy.signal.windows.blackmanharris`
    - `~scipy.signal.windows.nuttall`
    - `~scipy.signal.windows.barthann`
    - `~scipy.signal.windows.cosine`
    - `~scipy.signal.windows.exponential`
    - `~scipy.signal.windows.tukey`
    - `~scipy.signal.windows.taylor`
    - `~scipy.signal.windows.lanczos`
    - `~scipy.signal.windows.kaiser` (needs beta)
    - `~scipy.signal.windows.kaiser_bessel_derived` (needs beta)
    - `~scipy.signal.windows.gaussian` (needs standard deviation)
    - `~scipy.signal.windows.general_cosine` (needs weighting coefficients)
    - `~scipy.signal.windows.general_gaussian` (needs power, width)
    - `~scipy.signal.windows.general_hamming` (needs window coefficient)
    - `~scipy.signal.windows.dpss` (needs normalized half-bandwidth)
    - `~scipy.signal.windows.chebwin` (needs attenuation)

Rectangular

$\boldsymbol{RecWindow(n)=1}$

from scipy.signal import get_window

print(get_window('boxcar',5))

[1. 1. 1. 1. 1.]

RecWindow * sin(wt)

from scipy.signal import get_window
import numpy as np

t0, t1 = 0, 1
fs = 5
t = np.arange(t0,t1,1/fs)
f = 1
ft = np.sin(2*np.pi*f*t)
print(ft)

rec_window = get_window('boxcar',ft.size)
ft_window = ft * rec_window
print(ft_window)

[ 0.  0.95105652  0.58778525 -0.58778525 -0.95105652]
[ 0.  0.95105652  0.58778525 -0.58778525 -0.95105652]

Hanning

对称形式

$\boldsymbol{Hanning(n)=0.5-0.5\cos(\frac{2\pi{n}}{N-1}), (n=0,1,...,N-1)}$

from scipy.signal import get_window
import matplotlib.pyplot as plt
import numpy as np

N = 100
hanning_window = get_window('hann',N,fftbins=False)
plt.scatter(range(N),hanning_window,marker='*',s=6,c='b')
print(hanning_window[0:2],hanning_window[-2:])

window = [0.5-0.5*np.cos(2*np.pi*n/(N-1)) for n in range(N)]
plt.scatter(range(N),window,marker='o',s=6,c='none',edgecolors='r')
print(window[0:2],window[-2:])
plt.savefig('./f.jpg')

周期形式

$\boldsymbol{Hanning(n)=0.5-0.5\cos(\frac{2\pi{n}}{N}), (n=0,1,...,N-1)}$

from scipy.signal import get_window
import matplotlib.pyplot as plt
import numpy as np

N = 100
hanning_window = get_window('hann',N,fftbins=True)
plt.scatter(range(N),hanning_window,marker='*',s=6,c='b')
print(hanning_window[0:2],hanning_window[-2:])

window = [0.5-0.5*np.cos(2*np.pi*n/N) for n in range(N)]
plt.scatter(range(N),window,marker='o',s=6,c='none',edgecolors='r')
print(window[0:2],window[-2:])
plt.savefig('./f.jpg')

[0.         0.00098664] [0.00394265 0.00098664]
[0.0, 0.0009866357858642205] [0.0039426493427611176, 0.0009866357858642205]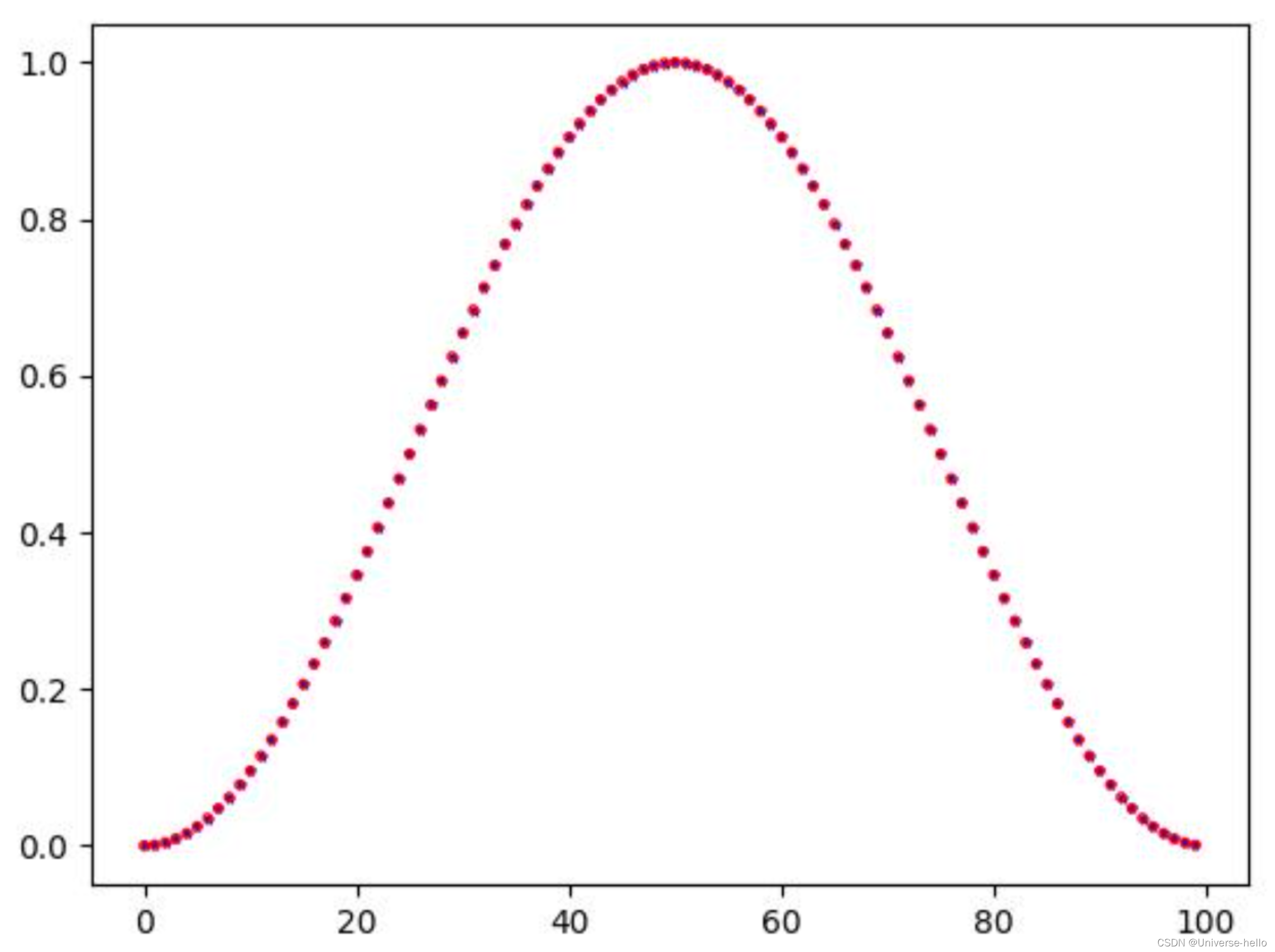

对称Hanning * sin(wt)

from scipy.signal import get_window
import matplotlib.pyplot as plt
import numpy as np

t0, t1 = 0,1
fs = 200
t = np.arange(t0,t1,1/fs)
f = 3
ft = np.sin(2*np.pi*f*t)
plt.scatter(t,ft,marker='.',s=6,c='b')

hanning_window = get_window('hann',ft.size,fftbins=False)
ft_window = ft * hanning_window

plt.scatter(t,ft_window,marker='*',s=6,c='r')
plt.savefig('./f.jpg')

Hamming

对称形式

$\boldsymbol{Hamming(n)=0.54-0.46\cos(\frac{2\pi{n}}{N-1}), (n=0,1,...,N-1)}$

from scipy.signal import get_window
import matplotlib.pyplot as plt
import numpy as np

N = 100
hamming_window = get_window('hamming',N,fftbins=False)
plt.scatter(range(N),hamming_window,marker='*',s=6,c='b')
print(hamming_window[0:2],hamming_window[-2:])

window = [0.54-0.46*np.cos(2*np.pi*n/(N-1)) for n in range(N)]
plt.scatter(range(N),window,marker='o',s=6,c='none',edgecolors='r')
print(window[0:2],window[-2:])
plt.savefig('./f.jpg')

周期形式

$\boldsymbol{Hamming(n)=0.54-0.46\cos(\frac{2\pi{n}}{N}), (n=0,1,...,N-1)}$

对称Hamming * sin(wt)

from scipy.signal import get_window
import matplotlib.pyplot as plt
import numpy as np

t0, t1 = 0,1
fs = 200
t = np.arange(t0,t1,1/fs)
f = 3
ft = np.sin(2*np.pi*f*t)
plt.scatter(t,ft,marker='.',s=6,c='b')

hamming_window = get_window('hamming',ft.size,fftbins=False)
ft_window = ft * hamming_window

plt.scatter(t,ft_window,marker='*',s=6,c='r')
plt.savefig('./f.jpg')

Blackman

对称形式

$\boldsymbol{Blackman(n)=0.42 - 0.5 \cos(\frac{2\pi{n}}{N-1}) + 0.08 \cos(\frac{4\pi{n}}{N-1}), (n=0,1,...,N-1)}$

from scipy.signal import get_window
import matplotlib.pyplot as plt
import numpy as np

N = 100
blackman_window = get_window('blackman',N,fftbins=False)
plt.scatter(range(N),blackman_window,marker='*',s=6,c='b')
print(blackman_window[0:2],blackman_window[-2:])

window = [0.42-0.5*np.cos(2*np.pi*n/(N-1))+0.08*np.cos(4*np.pi*n/(N-1)) for n in range(N)]
plt.scatter(range(N),window,marker='o',s=6,c='none',edgecolors='r')
print(window[0:2],window[-2:])
plt.savefig('./f.jpg')

[-1.38777878e-17  3.63046791e-04] [ 3.63046791e-04 -1.38777878e-17]
[-1.3877787807814457e-17, 0.0003630467905213902] [0.00036304679052143185, -1.3877787807814457e-17]

周期形式

$\boldsymbol{Blackman(n)=0.42 - 0.5 \cos(\frac{2\pi{n}}{N}) + 0.08 \cos(\frac{4\pi{n}}{N}), (n=0,1,...,N-1)}$

对称Blackman * sin(wt)

from scipy.signal import get_window
import matplotlib.pyplot as plt
import numpy as np

t0, t1 = 0,1
fs = 200
t = np.arange(t0,t1,1/fs)
f = 3
ft = np.sin(2*np.pi*f*t)
plt.scatter(t,ft,marker='.',s=6,c='b')

blackman_window = get_window('blackman',ft.size,fftbins=False)
ft_window = ft * blackman_window

plt.scatter(t,ft_window,marker='*',s=6,c='r')
plt.savefig('./f.jpg')