信息安全数学基础（二）

信息安全数学基础

——第二章 同余

---

---

前言

下面讨论同余的性质，以对整数进行恰当分类。

---

提示：以下是本篇文章正文内容，下面案例可供参考，大多数都是自己整理的，适用于我自己，不一定适用于所有人

一、同余的概念及基本性质

1.1同余的概念

定义：给定一个正整数m.两个整数a,b叫做模m同余，如果a-b被m整除，或m|a-b，就记作a≡b（mod m）.否则就叫做模m不同余

1.2同余的判断

定理:设m是一个正整数，设a,b是两个整数，则a≡b（mod m）的充要条件是存在另一个整数q使得a = b + q·m

模同余的性质：
设m是一个正整数，则模m同余是等价关系，即
（1）自反性：对于任一整数a，有a≡a（mod m）
（2）对称性：若a≡b（mod m），则b≡a（mod m）
（3）传递性：若a≡b（mod m），b≡c（mod m），则a≡c（mod m）

例题：

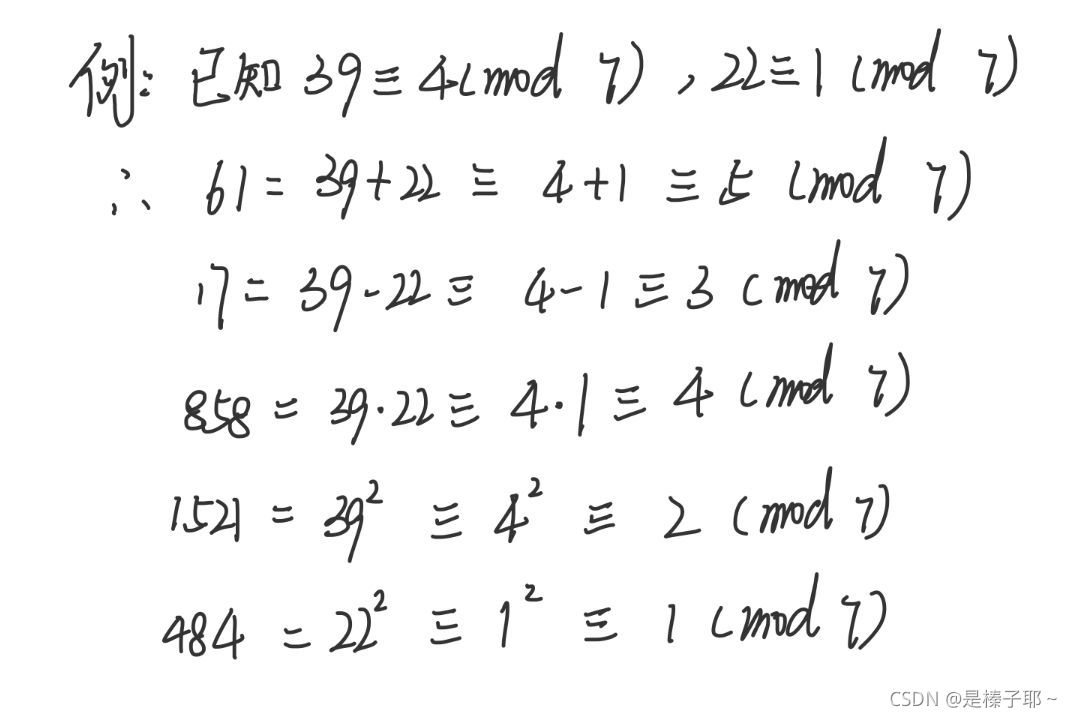
1.3同余的性质

定理：设m是一个正整数，设d·a≡d·b（mod m）.如果（d,m）= 1,则a≡b（mod m）.

定理：设m是一个正整数，设a≡b（mod m），d>0，则d·a≡d·b（mod d·m）

定理：设m是一个正整数，设a≡b（mod m）.如果d|m，则a≡b（mod d）

二、剩余类及完全剩余类

2.1剩余类与剩余

这个例题我就不上了，后面作业题里面有。

二、简化剩余系与欧拉函数

2.1欧拉函数

定义：设m是一个正整数，则m个整数1，2，…，m-1，m中与m互素的整数的个数，记作φ(m)，通常叫做欧拉函数

例题：

定理：

2.2简化剩余类与简化剩余系

定义：一个模m的剩余类叫做简化剩余类，如果该类中存在一个与m互素的剩余，这时，简化剩余类中的剩余叫简化剩余.

定义：设m是一个正整数，在模m的所有不同简化剩余类中，从每个类任取一个数组成的整数的集合，叫做模m的一个简化剩余系.

性质：设m>1是整数，a,b是模m的两个简化剩余，则它们的乘积也是简化剩余.

定理：设m是一个正整数，a是满足（a,m）=1的整数.如果k遍历模m的一个简化剩余系，则a·k也是遍历模m的一个简化剩余系.

定理：设m是一个正整数，a是满足（a,m）=1的整数，则存在唯一的整数a’，1≤a’<m，使得a·a’≡1（mod m）.

2.3欧拉函数的性质

定理：设m,n是互素的两个正整数，则φ(m·n) = φ(m)·φ(n)

例题：
φ(77)=φ(7)φ(11)=6·10=60
φ(30)=φ(2)φ(3)φ(5)=1·2·4=8

三、欧拉定理、费马小定理和Wilson定理

3.1欧拉定理

定理：设m是大于1的整数.如果a是满足（a,m）=1的整数，则a^φ(m)≡1（mod m）

例题：
设m = 11，a = 2.有（2，11）=1，φ(11)=10，所以2¹⁰≡1（mod 11）.

3.2费马小定理

定理：设p是一个素数，则对任意整数a，有a^p ≡ a (mod p)

推论：设p是一个素数，则对任意整数a，以及对任意整数t,k，有a^（t+k·（p-1）） ≡ a ^t (mod p)

3.3Wilson定理

定理：设p是一个素数，则（p-1）！≡ -1（mod p）

3.4模重复平方计算法

这些符号绕得有点晕，上例题：

---

四、习题

4.1写出模9的一个完全剩余系，它的每个数是基奇数

4.2证明：当m>2时，0²，1²，……，（m-1）²一定不是模m的完全剩余系.

4.3设p为素数.证明：如果a² ≡ b²（mod p），则p|a-b或p|a+b.

4.4证明：如果n是正整数，那么 1+2+3+……+（n-1）≡ 0（mod n）

4.5 证明：如果n是正整数，那么 1³+2³+3³+……+（n-1）³≡ 0（mod n）

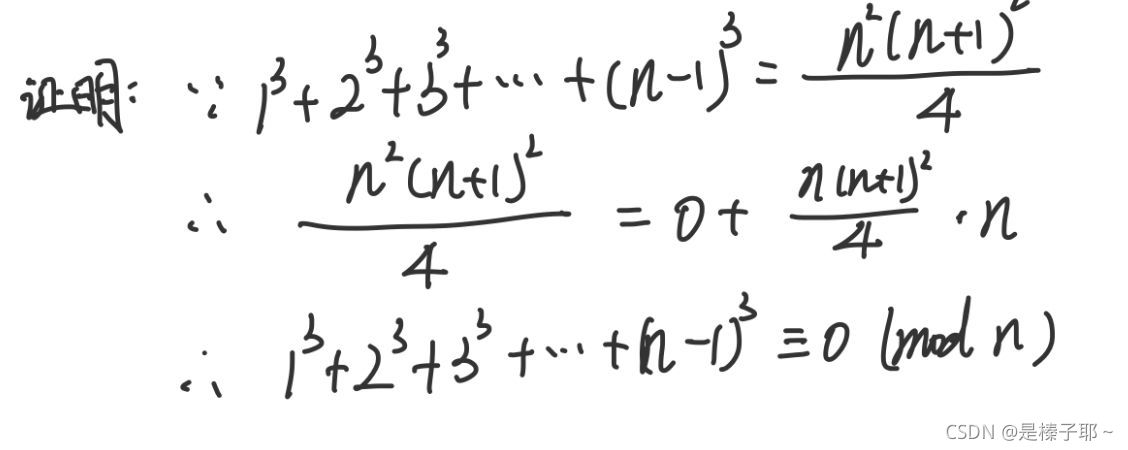
4.6 运用Wilson定理，求8·9·10·11·12·13（mod 7）

4.7 证明：如果a是整数，且（a，3）=1，那么a⁷ ≡ a（mod 63）

4.8 证明：如果a是与32760互素的整数，那么a¹² ≡ 1（mod 32760）