严蔚敏版数据结构——树和二叉树的常见知识点（持续更新……

基本术语：

• 节点的度：节点具有的子树的个数
• 树的度：树的节点的度的最大值
• 非终端节点：除叶子结点以外的所有点，又叫分支节点
• 内部节点：出叶子结点和根结点外的所有的点
• 树的深度：树中结点的最大层次
• 森林： 由若干棵互不相交的树的集合。

二叉树

定义：

每个节点最多只有两个分支的树，可以为空树

特点：

• 每个节点至多俩子树，即没有节点的度大于2
• 有左右子树之分，不可颠倒

满二叉树：

深度为 k 且含有$2^k-1$个节点的二叉树

其每一层上的节点树都是最大节点数，第 i 层有 $2^{i-1}$个节点

可以从上到下从左到右依次编号

完全二叉树：

深度为k，有n个节点，当且仅当其每个节点都与深度为k的满二叉树中编号从1到n的节点一一对应

• 叶子结点只能出现在最后两层

性质：

• 第 i 层至多有 $2^{i-1}$个节点

• 深度为 k 的二叉树至多有$2^k-1$个节点

• 对于任意一棵二叉树，满足 n0 = n2 + 1

  证明： 树的总节点 n = n0 + n1 + n2

  同样的，n = n0 * 0 + n1 * 1 + n2 * 2 + 1

  二式化简得到：n0 = n2 + 1

• 具有n个节点的完全二叉树具有的深度为：$\lfloor {\log }_{2}n\rfloor$ + 1

• 编号规则类似于线段树，左儿子等于父节点乘2，右儿子等于父节点乘2 + 1

二叉树的存储结构：

• 顺序存储：仅适用于完全二叉树，即像线段树那样用数组存下标

• 链式存储：

  二叉链表：数据域 + 左儿子指针 + 右儿子指针

  三叉链表：数据域 + 左儿子指针 + 右儿子指针 + 父亲指针

  n 个节点的二叉链表中有 n + 1 个空链域，证明如下：

  n0 = n2 + 1, 度为0的节点，的左右子树均空，故空链域为2 * (n2 + 1) ，同样的度为1的节点，空链域为1 * n1

  相加得到：n1 + n2 * 2 + 2 = (n1 + n2 * 2 + 1) + 1 = n + 1

  证毕

二叉树的遍历：

前序遍历：中左右

中序遍历：左中右

后序遍历：左右中

前序+中序 ——>后序

后序+中序 ——>前序

前序+后序一般不能推出中序，因为不知道左右子树的分界点

例题：

1. 前序：ABCDEFGH， 中序：BDCEAFHG 求后序

• 解题方法：因为前序的第一个必为根结点，所以去中序中找这个点，其左边的就为左子树，右边的就是右子树，再看这找到的左子树，就可以去前序中找到这几个字母，其中的第一个就是这个左子树的根节点，然后就一直这样找下去即可

思路：

• 先序里面，最先出现的是根节点，所以A就是根节点

• 中序里面，根节点A在中间，所以A的左边BDCE是左子树，A的右边FHG是右子树

• 先序里面，A的左子树B最先出现，所以B是左子树的根节点

• 中序里面，根节点B的左边没有结点，所以B的左子树为空，即DCE是B的右子树

• 先序里面，B的右子树C最先出现，所以C是右子树的根节点

• 中序里面，D在C的左边，E在C的右边，所以D是C的左子树，E是C的右子树

至此，A的左子树还原完毕

• 先序里面，A的右子树F最先出现，所以F是根节点

• 中序里面，根节点F的左边没有结点，所以F的左子树为空，即HG是F的右子树

• 先序里面，F的右子树G最先出现，所以G是根节点

• 中序里面，根节点G的左边有结点H，所以H是G的左子树

• 至此，A的二叉树还原完毕

即原始二叉树的后序为：D-E-C-B-H-G-F-A

2. 中序：BDCEAFHG

   后序：DECBHGFA

• 后序里面，最后出现的是根节点，所以A是根节点

• 中序里面，根节点A在中间，所以A的左边BDCE是左子树，A的右边FHG是右子树

• 后序里面，A的左子树B最后出现，所以B是左子树的根节点

• 中序里面，根节点B的左边没有结点，所以B的左子树为空，B的右子树是DCE

• 后序里面，B的右子树C最后出现，所以C是根节点

• 中序里面，根节点C的左边是E，所以E是C的左子树，C的右边是E，所以E是C的右子树

至此A的左子树还原完毕

• 后序里面，A的右子树F最后出现，所以F是根节点

• 中序里面，根节点F左边没有结点，所以F的左子树为空，F的右子树为HG

• 后序里面，F的右子树G最后出现，所以G是根节点

• 中序里面，G的左子树为H，G的右边没有结点，所以G的右子树为空

• 至此，A的二叉树还原完毕

所以先序为：A-B-C-D-E-F-G-H

先序遍历建立二叉链表

主要思想就是递归

先中后左再右

void built(bitlink &T){
    char c;
    cin>>c;
    if(c == '#'){//如果是#则表示该节点为空
        T = NULL;
    }
    else{
        T = (bitlink)malloc(sizeof(tnode));//申请空间
        T->data = c;
        built(T->lchild);//建立左子树
        built(T->rchild);//建立右子树
    }
}

改变递归顺序就可以实现其他顺序的建树

线索二叉树

先谈谈为什么搞这个线索二叉树……

其实是因为使用两个指针的二叉链表浪费的空间有点大，n 个节点的空间会浪费n + 1 的链域空间，大佬们看他不爽，所以线索二叉树诞生了（压根不考虑我们这些学生滴感受啊(╥﹏╥)

结构：

lchild	LTag	Data	RTag	Child

其中，LTag和Rtag为0或1，为0的时候表示该节点的左儿子或右儿子，为1时表示该节点的前驱或后继

画图的时候，LTag和Rtag为0时用实线，为1时用虚线

中序线索化时，中序序列的第一个节点的lchild和最后一个节点rchild指向头节点，而头节点指向树的根节点

树的存储结构

• 双亲表示法，只有一个双亲指针和一个数据域

• 孩子表示法

  1. 数据域 + k个孩子指针
  2. 数据域 + 度域 + k个孩子指针（度域为k）

• 孩子兄弟表示法，一个数据域，一个孩子节点，一个兄弟节点

  也就是将树二叉化了

森林和二叉树的转换

森林转换成二叉树：

• 转换：先把每一颗树转换成二叉树

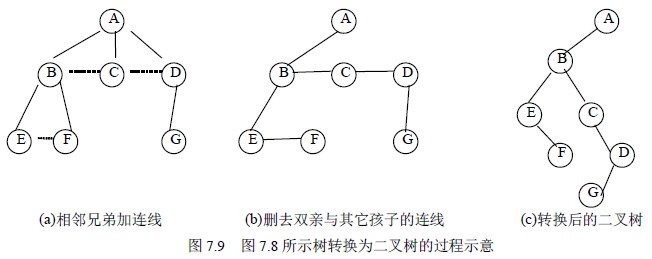
• 连线：第一棵二叉树不变，从第二棵二叉树开始，依次将后一棵二叉树的根节点作为前一棵二叉树根节点的右孩子，用线连起来

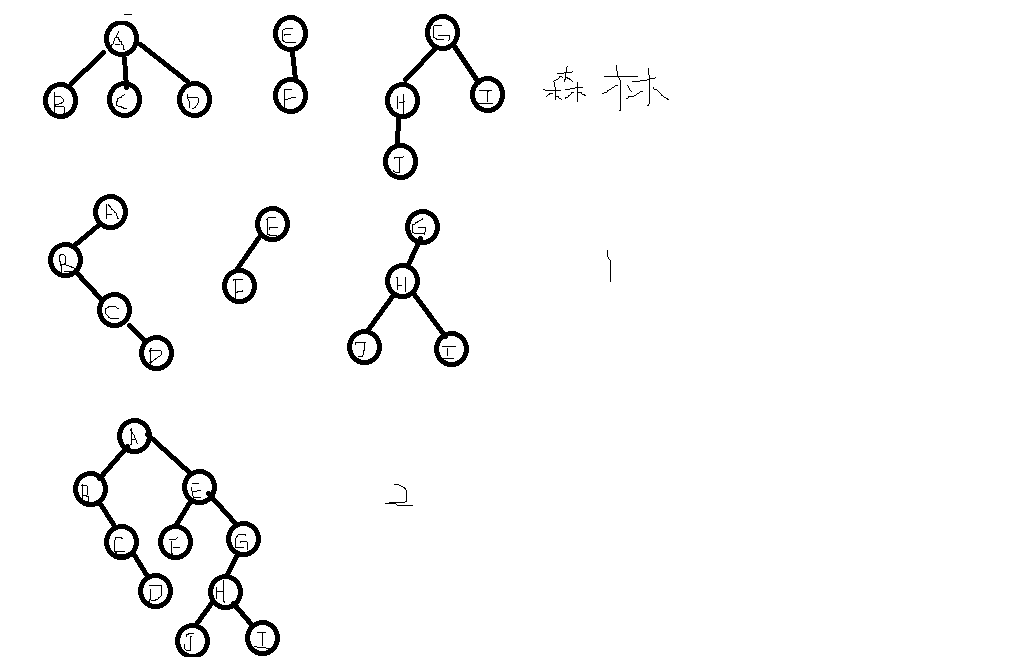
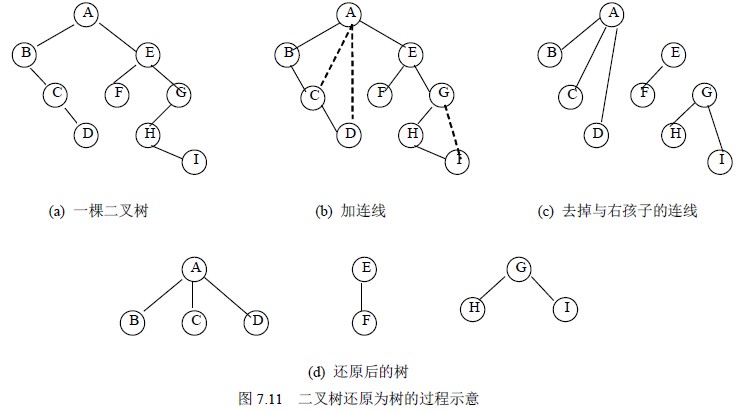
二叉树转换成森林

“左儿子右兄弟”

• 若某结点是其双亲的左孩子，则把该结点的右孩子、右孩子的右孩子……都与该结点的双亲结点用线连起来；
• 删去原二叉树中所有的双亲结点与右孩子结点的连线；
• 整理由前两步所得到的树或森林，使之结构层次分明。

哈夫曼树

定义：

哈夫曼树又称最优树，是一类带权路径最短的树

基本概念：

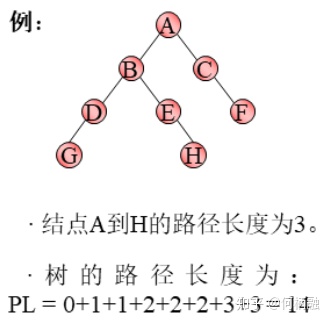
• 路径：一个节点到另一个节点都分之构成这两个节点之间的路径

• 路径长度：一个节点到另一个节点之间的分支数目（简单说就是从这个点到那个点经过几条边）

• 树的路径长度：从树根到每一个节点的路径长度之和

• 节点的带权路径长度：该节点到树根之间路径长度与节点上权的乘积

• 树的带权路径长度：树中所有叶子节点的带权路径长度之和

  

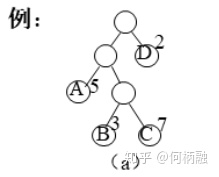
算出来的值最小的二叉树就称作最优二叉树或哈夫曼树。

如何构造？

每次取权值最小的点去造树，再将造出来的树的权值扔回去继续选俩最小的，一直这样下去……

数据结构作业6

#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <sstream>
#include <map>
#include <set>
using  namespace std;
#define inf 0x3f3f3f3f
#define MAX 100000 + 50
#define endl '\n'
#define mod 13331
#define io ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
#define mem(a,b) memset((a),(b),sizeof(a))
typedef  long long ll ;
//不开longlong见祖宗！
inline int IntRead(){char ch = getchar();int s = 0, w = 1;while(ch < '0' || ch > '9'){if(ch == '-') w = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){s = s * 10 + ch - '0';ch = getchar();}return s * w;}
inline void write(int x){if (x < 0) {x = ~x + 1; putchar('-');}if (x > 9){write(x / 10);}putchar(x % 10 + '0');}



typedef struct tnode{
    char data;
    struct tnode *lchild, *rchild;
}bitree, *bitlink;


void init(bitlink &T){
    T = (bitlink)malloc(sizeof(tnode));
    T->lchild = NULL;
    T->rchild = NULL;
}

void built(bitlink &T){
    char c;
    cin>>c;
    if(c == '#'){
        T = NULL;
    }
    else{
        T = (bitlink)malloc(sizeof(tnode));
        T->data = c;
        built(T->lchild);
        built(T->rchild);
    }
}

void Pre_Print_Tree(bitlink T){
    cout<<T->data;
    if(T->lchild != NULL)Pre_Print_Tree(T->lchild);
    if(T->rchild != NULL)Pre_Print_Tree(T->rchild);
}

void Mid_Print_Tree(bitlink T){
    if(T->lchild != NULL)Mid_Print_Tree(T->lchild);
    cout<<T->data;
    if(T->rchild != NULL)Mid_Print_Tree(T->rchild);
}

void Tail_Print_Tree(bitlink T){
    if(T->lchild != NULL)Tail_Print_Tree(T->lchild);
    if(T->rchild != NULL)Tail_Print_Tree(T->rchild);
    cout<<T->data;
}

int Tree_getnum(bitlink T){
    int num = 0;
    if(T != NULL)++num;
    if(T->lchild != NULL)num += Tree_getnum(T->lchild);
    if(T->rchild != NULL)num += Tree_getnum(T->rchild);
    return num;
}

int Tree_getleafnum(bitlink T){
    int num = 0;
    if(T != NULL && T->lchild == NULL && T->rchild == NULL)++num;
    if(T->lchild != NULL)num += Tree_getleafnum(T->lchild);
    if(T->rchild != NULL)num += Tree_getleafnum(T->rchild);
    return num;
}

int main(){
    
    bitlink T;
    built(T);
    
    cout<<"前序遍历：";
    Pre_Print_Tree(T);
    cout<<endl;
    
    cout<<"中序遍历：";
    Mid_Print_Tree(T);
    cout<<endl;
    
    cout<<"后序遍历：";
    Tail_Print_Tree(T);
    cout<<endl;
    
    cout<<"该树具有的节点数为： ";
    cout<<Tree_getnum(T)<<endl;
    
    cout<<"该树具有的叶子节点数为： ";
    cout<<Tree_getleafnum(T)<<endl;
    return 0;
}