关于克拉默法则的一些理解

一、定义

含有n个未知数  的n个线性方程的方程组

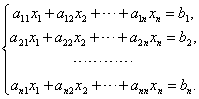
（1）

它的解可以用n阶行列式表示，即有

克拉默法则 如果线性方程组（1）的系数矩阵A的行列式不等于零，即

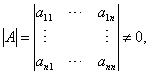
那么，方程组（1）有唯一解  ，  ，...，  ，其中  是把系数矩阵A中第  列的元素用方程组右端的常数项代替后所得到的n阶矩阵，

证 把方程组（1）写成矩阵方程  ，这里  为n阶矩阵，因  ，故  存在。

由  ，有  ，即  ，根据逆矩阵的唯一性，知  是方程组（1）的唯一的解向量。

由逆矩阵公式  ，有  ，即

     .

克拉默法则解决的是方程个数与未知数个数相等并且系数行列式不等于零的线性方程组。

 

二、对于非齐次线性方程与非齐次线性方程的克拉默法则的理解记忆方法

在非齐次线性方程组中，有克拉默法则的定义可知 D=系数行列式aij的值，x1=D1/D,x2=D2/D…以此类推xn=Dn/D，其中D1,D2…Dn为将非齐次线性方程的非齐次项替换掉系数行列式中aij一列的值，例如D1为将非齐次项替换掉a1j这一列。
1）由此定义，我们可以这样理解记忆，当系数行列式不为0时，即x1=D1/D的分母不为0，则每个x未知数都可以算出一个对应的值，即为书中所说的D不等于0，有唯一解
2）当D-0时，因为分母等于0，由高数定义可知，当分母趋向于0，分子为常数，则此数极限趋于无穷。即该方程组有无穷多解。

 

推广到齐次线性方程组中，当把齐次方程组当作非齐次方程组时，他的非齐次项即为0，像上述的非齐次方程组的克拉默法则那样代到里面去求解，则因为系数行列式含有0的列向量，则系数行列式必为0，即x1=D1/D中的D1必为0，说明无论怎么样的齐次方程组，他的D1~Dn必为0，所以我们来讨论他的分母，1）当分母不为0时，毫无疑问，所有的x都为0，即为方程组只有一个解且为0解，2）当分母为0时，由极限的定义可知，0比0型是一个未定式，有无穷多的可能，即为方程组有无穷多解。