毫米波雷达干涉测角-长短基线法：MATLAB仿真与实现

雷达科研han

已于 2024-03-23 16:52:56 修改

阅读量1.7k

点赞数 41

文章标签： matlab 算法信号处理

于 2024-03-23 16:43:25 首次发布

本文链接：https://blog.csdn.net/weixin_51532466/article/details/136967055

版权

导言

毫米波雷达干涉测角技术是一种常用于目标定位和测量的高精度雷达技术。本文将介绍毫米波雷达干涉测角的基本原理，基于长短基线法进行干涉测角，并通过MATLAB仿真演示其工作过程。读者将通过本文了解毫米波雷达干涉测角技术的原理和实现方法，以及如何使用MATLAB进行仿真和验证。

一、毫米波雷达干涉测角技术介绍

毫米波雷达干涉测角技术是一种利用多个接收天线或阵列来接收雷达信号，并通过相位差来测量目标方向的技术。其主要特点是能够实现高精度的方向测量，适用于目标定位、无人机导航、车辆避撞等领域。

二、毫米波雷达干涉测角的基本原理

毫米波雷达干涉测角的基本原理是利用接收天线或阵列之间的相位差来测量目标的方向。当雷达信号被目标反射后，经过不同路径到达接收天线或阵列，导致接收到的信号存在相位差。通过测量这种相位差，可以计算出目标的方向。

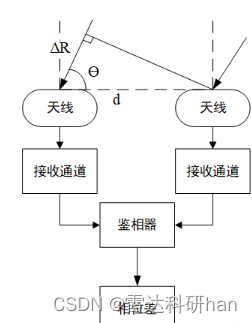
天线阵元在接收目标回波信号时，可将远场波看作平行波，则回波到达各天线阵元时存在路程差，而干涉仪测角是通过天线阵元间接收到目标回波的波程差来计算目标角度。需要注意的是，当波程差大于 $\lambda /2$ 时，天线阵元间的相位差会超过 180°，从而出现测角模糊。为了避免测角模糊，采用长短基线联合测向的方法解决测角模糊问题。

详细原理请看哔哩哔哩视频：阵列天线波束形成原理，相位差φ、方向角θ有啥关系？_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1NW4y1u7au

三、长短基线干涉测角法

长短基线在测角过程中存在模糊但测角精度高，短基线测角时不存在模糊但精度较低，将两者进行联合测角，即可实现无模糊的高精度测角。

长基线相位差：

$\varphi _{13}=\frac{2\pi d_{13}}{\lambda }\sin \theta$

短基线相位差：

$\varphi _{12}=\frac{2\pi d_{12}}{\lambda }\sin \theta$

由上式可知 $\varphi _{13}$ 和 $\varphi _{12}$ 满足如下关系

$\frac{\varphi_{13}}{\varphi_{12}}=\frac{d_{13}}{d_{12}}=m$

由于 $\varphi _{13}$ ,存在测向模糊，而 $\varphi _{12}$ ，不会出现测向模糊，因此真实相位差为

$\varphi _{13}=2k\pi +\phi _{13}$

$\varphi _{12}=\phi _{12}$

由上式可求得k

$2k\pi +\phi _{13}=m\phi _{12}$

$k=\frac{m\phi _{12}-\phi 13}{2\pi }$

由长基线干涉测角公式可得目标方位 $\theta$

$2k\pi +\phi _{13}=\frac{2\pi d_{13}}{\lambda }\sin \theta$

四、MATLAB仿真与实现

接下来，我们将通过MATLAB进行毫米波雷达干涉测角的仿真演示。首先，我们需要定义雷达系统的参数，包括工作频率、天线阵列结构、目标距离等。然后，我们利用MATLAB的信号处理和仿真工具箱，模拟雷达信号的传播和接收过程，并计算出接收天线或阵列之间的相位差。最后，根据相位差数据，利用干涉测角算法计算目标的方向。

以下是MATLAB代码的示例：

% clc;
clear all;
close all;
%% 雷达信号参数

% 定义常量
c= 3e8; % m/s, 光速
radar_f = 76e9;%频率
lamda = c/radar_f;%波长
%% 定义入射信号参数
incident_angle_deg = 3.5; % 入射角度
incident_angle_rad = deg2rad(incident_angle_deg); % 将角度转换为弧度
pw = 0.5e-6;%脉宽（随机设置，可以设置成FMCC体制）

disp(['实际输入的目标方位角：', num2str(incident_angle_deg), ' 角度']);
%% 天线阵列参数
num_antennas = 4; % 天线数量

% 定义天线间隔
spacing=lamda/2;%天线间隔为半波长
long_baseline = 3*spacing; % 长基线长度，3个天线间隔
short_baseline = spacing; % 短基线长度，1个天线间隔

%% 干涉仪参数
fs=760e9;
t=0:1/fs:pw-1/fs;
%% 距离差求取时延差
tau1=short_baseline*sind(incident_angle_deg)/c;
tau2=long_baseline *sind(incident_angle_deg)/c;
%% 到达三个天线的信号
x1=exp(1i*2*pi*radar_f*t);
x2=exp(1i*2*pi*radar_f*(t-tau1));
x3=exp(1i*2*pi*radar_f*(t-tau2));

%% 天线间的相位差
%%%利用共轭复乘得相位差
diffPhase_short = mean(angle(x1.*conj(x2)));%%获取1，2号天线的相位差，保证无模糊
diffPhase_long= mean(angle(x1.*conj(x3)));%%获取1，3号天线的相位差，保证精确估计DOA

% 显示结果
disp(['短基线相位差：', num2str(diffPhase_short), ' 弧度']);
disp(['长基线相位差：', num2str(diffPhase_long), ' 弧度']);

%% DOA估计
%%先求取2kπ的周期数k，后利用长基线-干涉测角公式求取目标方位
k = (long_baseline*diffPhase_short/short_baseline -diffPhase_long)/(2*pi);%求周期数k
C1 = lamda*(diffPhase_long+k*2*pi)/(2*pi*long_baseline);%利用干涉公式求sin
theta = asin(C1)*360/(2*pi);
disp(['干涉测角解算的目标方位角：', num2str(theta), ' 角度']);

MATLAB代码旨在模拟雷达系统中利用干涉测向技术来估计目标的方位角度。具体而言，代码的执行过程包括以下几个步骤：

雷达信号参数定义：确定了光速和雷达的工作频率，进而计算得到了波长。
入射信号参数定义：设置了目标的入射角度，并将其转换为弧度。
天线阵列参数定义：确定了天线数量和天线之间的间隔，包括短基线和长基线的长度。
干涉仪参数定义：设置了采样频率，并生成了时间序列。
计算时延差：根据入射角度、天线间隔和光速，计算了到达不同天线的信号的时延差。
生成到达三个天线的信号：通过考虑时延差，生成了到达第一个、第二个和第三个天线的信号。
计算天线间的相位差：利用生成的信号，计算了短基线和长基线的天线间相位差。
DOA估计：根据天线间的相位差，利用干涉测向公式估算了目标的方位角度。
结果显示：将计算得到的短基线和长基线的相位差以及估算得到的目标方位角度显示在命令窗口中。

结论

毫米波雷达干涉测角技术是一种重要的雷达定位技术，能够实现高精度的目标方向测量。通过MATLAB仿真，我们可以模拟毫米波雷达系统的工作过程，并实现长短基线干涉测角算法，从而验证其性能和准确性。读者可以根据本文提供的仿真代码，进一步研究和应用毫米波雷达干涉测角技术。

雷达科研han

关注

41
点赞
踩
45

收藏

觉得还不错? 一键收藏
4
评论
毫米波雷达干涉测角-长短基线法：MATLAB仿真与实现

毫米波雷达干涉测角技术是一种利用多个接收天线或阵列来接收雷达信号，并通过相位差来测量目标方向的技术。其主要特点是能够实现高精度的方向测量，适用于目标定位、无人机导航、车辆避撞等领域。本文基于长短基线法，用MATLAB仿真验证毫米波雷达干涉测角。
复制链接

扫一扫