【运筹优化】运输问题建模 + Java调用Cplex求解

---

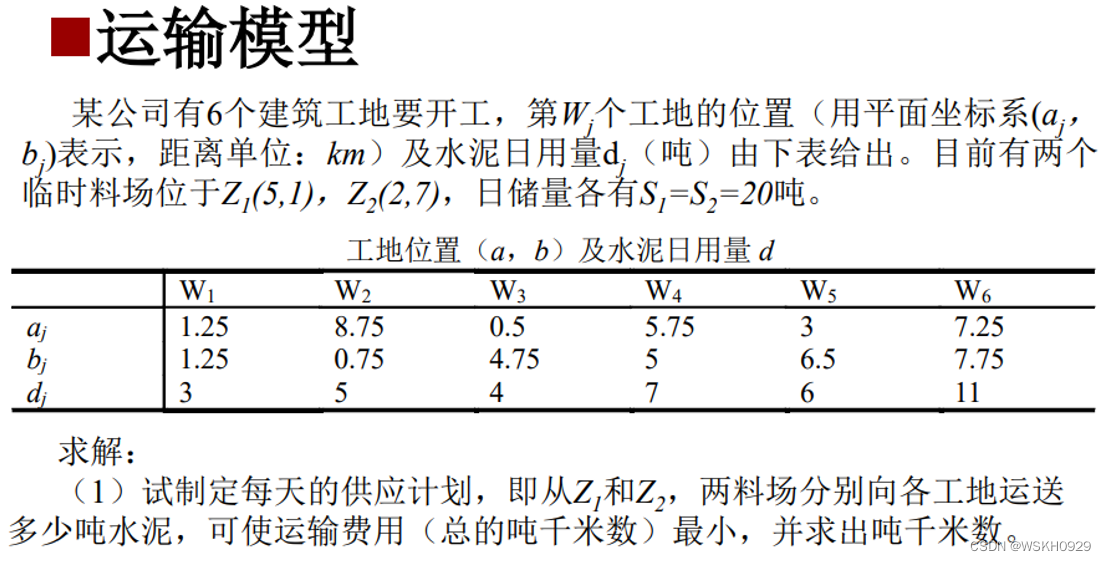
一、问题描述

运输问题(transportation problem）一般是研究把某种商品从若干个产地运至若干个销地而使总运费最小的一类问题。

本博客将根据下面的例题，介绍运输问题的建模和求解

---

二、思路分析

在料场与工地之间计算一个距离弧，然后将分配到弧上的运输量作为决策变量，从而建立线性规划模型调用Cplex求解。

---

三、建模方案

令$x_{ij}$为料场$i=(1,2,...,n)$向工地$j=(1,2,...,m)$运输的水泥量（吨），$d_{ij}$为料场$i$到工地$j$的欧几里得距离（km），$c_i$为料场$i$的日储量（吨），$s_j$为工地$j$的日用量（吨），则问题（1）可以被建模为如下的线性规划模型：

---

四、Java调用Cplex代码

import ilog.concert.IloLinearNumExpr;
import ilog.concert.IloNumVar;
import ilog.cplex.IloCplex;
import lombok.AllArgsConstructor;

import java.util.ArrayList;
import java.util.List;

/**
 * @Author：WSKH
 * @ClassName：Answer1
 * @Description：
 * @Time：2023/8/15/9:49
 * @Email：1187560563@qq.com
 * @Blog：wskh0929.blog.csdn.net
 */
public class Answer1 {
    /**
     * 料场对象
     */
    @AllArgsConstructor
    static class Stockyard {
        /**
         * x,y坐标和储量c
         */
        double x, y, c;
    }

    /**
     * 工地对象
     */
    @AllArgsConstructor
    static class ConstructionSite {
        /**
         * x,y坐标和需求d
         */
        double x, y, d;
    }

    private static double calcDistance(double x1, double y1, double x2, double y2) {
        return Math.sqrt(Math.pow(x1 - x2, 2) + Math.pow(y1 - y2, 2));
    }

    public static void main(String[] args) throws Exception {
        // 浮点型精度误差
        double EPS = 1e-06;
        // 料场列表
        List<Stockyard> stockyardList = new ArrayList<>();
        stockyardList.add(new Stockyard(5, 1, 20));
        stockyardList.add(new Stockyard(2, 7, 20));
        // 工地列表
        List<ConstructionSite> constructionSiteList = new ArrayList<>();
        constructionSiteList.add(new ConstructionSite(1.25, 1.25, 3));
        constructionSiteList.add(new ConstructionSite(8.75, 0.75, 5));
        constructionSiteList.add(new ConstructionSite(0.5, 4.75, 4));
        constructionSiteList.add(new ConstructionSite(5.75, 5, 7));
        constructionSiteList.add(new ConstructionSite(3, 6.5, 6));
        constructionSiteList.add(new ConstructionSite(7.25, 7.75, 11));
        // 计算距离矩阵
        double[][] distanceMatrix = new double[stockyardList.size()][constructionSiteList.size()];
        for (int i = 0; i < distanceMatrix.length; i++) {
            Stockyard stockyard = stockyardList.get(i);
            for (int j = 0; j < distanceMatrix[i].length; j++) {
                ConstructionSite constructionSite = constructionSiteList.get(j);
                distanceMatrix[i][j] = calcDistance(stockyard.x, stockyard.y, constructionSite.x, constructionSite.y);
            }
        }
        // 开始建模
        IloCplex cplex = new IloCplex();
        // 声明变量
        IloNumVar[][] x = new IloNumVar[stockyardList.size()][constructionSiteList.size()];
        for (int i = 0; i < x.length; i++) {
            for (int j = 0; j < x[i].length; j++) {
                x[i][j] = cplex.numVar(0, Math.min(stockyardList.get(i).c, constructionSiteList.get(j).d));
            }
        }
        // 构造约束1：必须满足每个工地的需求
        for (int j = 0; j < constructionSiteList.size(); j++) {
            IloLinearNumExpr expr = cplex.linearNumExpr();
            for (int i = 0; i < x.length; i++) {
                expr.addTerm(1, x[i][j]);
            }
            cplex.addEq(expr, constructionSiteList.get(j).d);
        }
        // 构造约束2：不能超过每个料场的储量
        for (int i = 0; i < stockyardList.size(); i++) {
            cplex.addLe(cplex.sum(x[i]), stockyardList.get(i).c);
        }
        // 声明目标函数
        IloLinearNumExpr target = cplex.linearNumExpr();
        for (int i = 0; i < x.length; i++) {
            for (int j = 0; j < x[i].length; j++) {
                target.addTerm(distanceMatrix[i][j], x[i][j]);
            }
        }
        cplex.addMinimize(target);
        // 配置cplex
        cplex.setOut(null);
        cplex.setWarning(null);
        cplex.setParam(IloCplex.DoubleParam.EpOpt, EPS);
        // 开始求解
        long s = System.currentTimeMillis();
        if (cplex.solve()) {
            System.out.println("最小吨千米数为: " + cplex.getObjValue());
            for (int i = 0; i < stockyardList.size(); i++) {
                for (int j = 0; j < x[i].length; j++) {
                    double xValue = cplex.getValue(x[i][j]);
                    if (xValue > EPS) {
                        System.out.println("料场" + (i + 1) + "向工地" + (j + 1) + "运输" + xValue + "吨水泥");
                    }
                }
            }
            System.out.println("求解用时: " + (System.currentTimeMillis() - s) / 1000d + " s");
        } else {
            System.err.println("此题无解");
        }
        // 结束模型
        cplex.end();
    }
}

---

五、输出结果

最小吨千米数为: 136.22751988318154
料场1向工地1运输3.0吨水泥
料场1向工地2运输5.0吨水泥
料场1向工地4运输7.0吨水泥
料场1向工地6运输1.0吨水泥
料场2向工地3运输4.0吨水泥
料场2向工地5运输6.0吨水泥
料场2向工地6运输10.0吨水泥
求解用时: 0.002 s