从零开始的深度学习(二):图卷积神经网络公式推导
1. 节点间消息传递计算方法
- 每一个节点的信息由自身和邻接节点的信息所组成
- 其中 W j W_j Wj代表可学习参数
- j ∈ N i j\in N_i j∈Ni代报 i i i节点中,所有与值相邻的邻接结点
- 汇总函数表示自身 h i h_i hi的权重再加上与自身相邻的所有邻接节点乘上可学习参数后再经过激活函数即可得到新的节点属性
- 同时会中函数中还有不同方式:
M
e
a
n
(平均)、
S
u
m
(求和)、
M
a
x
(最大值)、
M
i
n
(最小值)
Mean(平均)、Sum(求和)、Max(最大值)、Min(最小值)
Mean(平均)、Sum(求和)、Max(最大值)、Min(最小值)

2. 图卷积神经网络公式推导

-
每个图的基本组成:
邻接矩阵A、度矩阵D、特征矩阵X- 其中邻接矩阵中代表那两个节点通过边进行相连
- 度矩阵中的数字代表每个节点存在多少个邻居节点
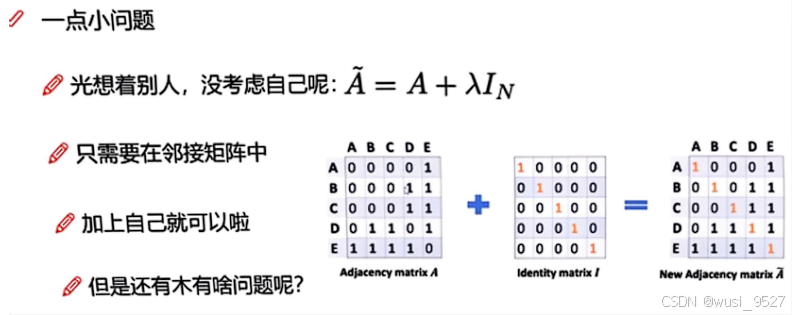
-
通过在邻接矩阵中添加自身节点来更新临界矩阵。在代码中也可以通过设置参数的方式实现上述更新邻接矩阵的操作

-
在邻接矩阵变换后,因为每个节点通过边连接的节点包括了自己,故度矩阵 D D D也要更新得到 D ~ \tilde{D} D~。因为在要平均每个节点传输给目标节点的数据,故需要对度矩阵进行归一化得到 D ~ − 1 \tilde{D}^{-1} D~−1
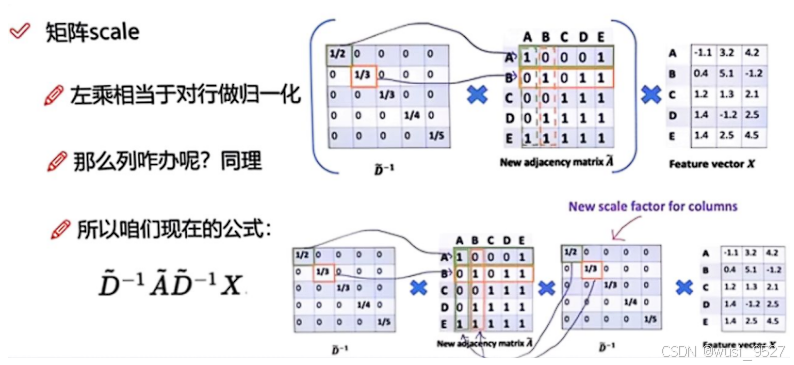
-
将归一化后的度矩阵 D ~ − 1 \tilde{D}^{-1} D~−1对临界矩阵 A ~ \tilde{A} A~进行左乘右乘后便可实现对行、列归一化

-
若是直接左乘右乘度矩阵 D ~ − 1 \tilde{D}^{-1} D~−1,相当于乘上了平方,故需要对度矩阵中的每个元素进行开方

-
诸如像一个社交网络,其中红色方框内是 v i v_i vi,绿色方框内是 v j v_j vj。若是需要求解 v i v_i vi的特征,因为 v i v_i vi的度非常小,证明自身的特征对于计算新的特征影响非常大。但是因为 v j v_j vj的度 d e g ( v j ) deg(v_j) deg(vj)非常大,使用能传输给 v i v_i vi的特征非常少
-
最终 1 deg ( v i ) ⋅ deg ( v j ) = D ^ − 1 2 A ^ D ^ − 1 2 \frac{1}{\sqrt{\text{deg}(v_i)} \cdot \sqrt{\text{deg}(v_j)}} = \hat{D}^{-\frac{1}{2}} \hat{A} \hat{D}^{-\frac{1}{2}} deg(vi)⋅deg(vj)1=D^−21A^D^−21,同时令邻接矩阵 X X X等于权重参数乘上节点 i i i的所有邻居节点(包括自己),即为 X = W ⊤ ⋅ x j X=W^{\top}\cdot x_{j} X=W⊤⋅xj, j ∈ N ( i ) ∪ { i } j\in\mathcal{N}(i)\cup\{i\} j∈N(i)∪{i}。其中 N ( i ) N(i) N(i)表示 i i i的所有邻居矩阵
-
最终得到 D ~ − 1 / 2 A ~ D ~ − 1 / 2 X = ∑ j ∈ N ( i ) ∪ { i } 1 deg ( i ) ⋅ deg ( j ) ⋅ ( W ⊤ ⋅ x j ) + b \tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} X=\sum_{j\in\mathcal{N}(i)\cup\{i\}}\frac{1}{\sqrt{\operatorname{deg}(i)}\cdot\sqrt{\operatorname{deg}(j)}}\cdot\left(W^{\top}\cdot x_{j}\right)+b D~−1/2A~D~−1/2X=∑j∈N(i)∪{i}deg(i)⋅deg(j)1⋅(W⊤⋅xj)+b
- 其中 b 代表添加的偏差
- 上述右侧公式即为图卷积神经网络的基础公式
3. 图神经网络代码实现
3.1 节点和边的创立
- 图神经网络用于对节点以及节点之间的关系(边)进行建模。单个图使用 torch_geometric.data.Data 的方法进行建模,下属是该方法包含的属性
- data.x:形状为 [num_nodes, num_node_features] 的节点特征矩阵
- data.edge_index:形状为 [2, num_edges] 且类型 torch.long 的 COO 格式的图形连接
- data.edge_attr:形状为 [num_edges, num_edge_features] 的边特征矩阵
- data.y:要训练的目标(可以具有任意形状),例如,形状为 *[num_nodes, ] 的节点级目标或形状为 *[1, ] 的图形级目标
- data.pos:形状为 [num_nodes, num_dimensions] 的节点位置矩阵
- 上述属性中最为常用的为 data.x 以及 data.edge_index。
-
x 为是一个
[num_x, num_node_features]二维张量- 其中
num_x表示节点的数量 num_node_features表示每一个节点中含有的特征数量。
- 其中
-
edge_index是一个形状为[2, num_edges]的二维张量,其中:- 第一维(大小为 2)表示边的两个端点(即源节点和目标节点)的索引。具体来说:
edge_index[0, i]表示第i条边的源节点(起始节点)的索引。 - 第二维(大小为
num_edges)表示图中边的总数。具体来说:edge_index[1, i]表示第i条边的目标节点(终止节点)的索引。
- 第一维(大小为 2)表示边的两个端点(即源节点和目标节点)的索引。具体来说:
-
诸如下面这个简单图,包含三个节点和四条边。edge_index[0] 包含所有源节点的索引(0, 1, 1, 2),而
edge_index[1]包含所有目标节点的索引(1, 0, 2, 1)。因此,第一条边是 0-1,第二条边是 1-0,依此类推。同时 x 为[3,1],表示存在三个节点,每个属性内部含有一个特征

# 通过pytorch中的tensor类型来创建节点数据 x=torch.tensor([[-1],[0],[1]],dtype=torch.float) # 创建边数据 edge_index = torch.tensor([[0, 1, 1, 2], [1, 0, 2, 1]], dtype=torch.long)
-
3.2 图卷积神经网络GCN
-
数学公式分析: x i ( k ) = ∑ j ∈ N ( i ) ∪ { i } 1 deg ( i ) ⋅ deg ( j ) ⋅ ( W ⊤ ⋅ x j ( k − 1 ) ) + b x_{i}^ {(k)}=\sum_{j\in\mathcal{N}(i)\cup\{i\}}\frac{1}{\sqrt{\operatorname{deg}(i)}\cdot\sqrt{\operatorname{deg}(j)}}\cdot\left(W^{\top}\cdot x_{j}^{(k-1)}\right)+b xi(k)=∑j∈N(i)∪{i}deg(i)⋅deg(j)1⋅(W⊤⋅xj(k−1))+b
- ∑ j ∈ N ( i ) ∪ { i } \sum_{j\in\mathcal{N}(i)\cup\{i\}} ∑j∈N(i)∪{i}邻居节点特征的聚合: 对于每个节点 i i i, 公式首先考虑其邻居节点集合 N ( i ) \mathcal{N}(i) N(i) 以及节点 i i i 本身。
-
1
deg
(
i
)
⋅
deg
(
j
)
\frac{1}{\sqrt{\operatorname{deg}(i)}\cdot\sqrt{\operatorname{deg}(j)}}
deg(i)⋅deg(j)1:
- 对于每个邻居节点 j j j, 公式计算了一个加权的特征值, 其中权重由节点 i i i 和 j j j的度数(即连接的边数)的平方根的倒数决定。这个权重确保了度数较高的节点不会因为其大量的邻居而对聚合特征贡献过大。
- d e g ( i ) {deg}(i) deg(i)代表节点 i i i的邻居数量; d e g ( j ) deg(j) deg(j)代表节点 j j j的邻居数量。即它们各自连接的边的数量
- 特征的线性变换: 每个邻居节点 j j j的特征 x j ( k − 1 ) x_j^{(k-1)} xj(k−1)都会通过一个权重矩阵 W W W进行线性变换。这个权重矩阵是通过训练学习得到的,它决定了如何将邻居节点的特征组合成新的特征。
- 特征的聚合和更新: 所有邻居节点的加权和变换后的特征被相加, 然后加上一个偏置项 b b b。这个结果就是节点 i i i 在第 k k k层的新的特征 x i ( k ) x_i^{(k)} xi(k)。
-
代码实现:
-
初始化
- 使用
torch.empty(out_channels)创建一个未初始化的张量,其维度为out_channels,即与输出维度一致,然后将其转换为Parameter,以便在模型训练过程中对其进行优化。
def __init__(self, in_channels, out_channels): super().__init__(aggr='add') # "Add" aggregation (Step 5). self.lin = Linear(in_channels, out_channels, bias=False) self.bias = Parameter(torch.empty(out_channels)) self.reset_parameters() - 使用
-
前向传播
-
第一步: 将自环添加到邻接矩阵中。自环是连接节点到它自身的边,有助于保留节点自身的特征。
-
第二步: 调用初始化的线性变换函数对输入节点特征进行线性变换
-
第三步: 计算每个节点的度,并计算其的根的倒数
-
row, col = edge_index:分别获得邻接矩阵中的行和列,在此处,row,col分别获得edge_index的第一行和第二行,即为:row:包含所有边的起点节点集合;col:包含所有边的终点节点集合
edge_index=torch.tensor([[0,1,1,2], [1,0,2,1]],dtype=torch.long) row,col=edge_index print(f'row:{row},col:{col}') # 输出为:row:tensor([0, 1, 1, 2]),col:tensor([1, 0, 2, 1]) -
deg = degree(col, x.size(0), dtype=x.dtype):
col包含所有边的终点节点,x.size(0)是节点的数量。同时返回的数据类型与节点一样,如下图绿色节点所示,我需要考虑每一个节点作为边的目标节点数量以便更好得去计算节点的度,所以使用degree(col…)。

- 下述是求解节点的度函数degree中需要传入的形参
- index (LongTensor): 索引张量,表示节点的连接关系。
- num_nodes (int, optional): 节点的数量,即 index 中最大值加一。如果未指定,函数将自动推断。
- dtype (torch.dtype, optional): 返回张量所需的数据类型。如果未指定,则会自动选择一个合适的数据类型。
import torch from torch_geometric.utils import degree # 假设我们有一个边的索引表示,其中包含了指向节点 0、1 和 2 的边 edge_index = torch.tensor([0, 1, 2], dtype=torch.long) # 计算每个节点的度数 node_degrees = degree(edge_index, num_nodes=3) print(node_degrees) # 输出是 tensor([1., 1., 1.])
-
-
第四步: 使用函数propagate开始消息传递
-
propagate(edge_index, x=x, norm=norm):传入各项参数,同时采用默认聚合方式‘add’
- edge_index (LongTensor): 图的边索引,形状为 [2, num_edges],表示图中边的连接关系。
- x (Tensor, optional): 节点特征矩阵,形状为 [num_nodes, num_node_features],表示每个节点的特征向量。
- op (str, optional): 指定聚合操作的类型,例如 ‘add’, ‘mean’, ‘max’, ‘min’。默认为 ‘add’。
# 完整前向传播代码 def forward(self, x, edge_index): # x的形状为[N, in_channels] # edge_index 形状为 [2, E] # Step 1:添加自环到邻接矩阵中. edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0)) # Step 2: 对节点特征进行线性变换. x = self.lin(x) # Step 3: 计算归一化系数. row, col = edge_index deg = degree(col, x.size(0), dtype=x.dtype) deg_inv_sqrt = deg.pow(-0.5) # 将该度的下界定义为0 deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0 norm = deg_inv_sqrt[row] * deg_inv_sqrt[col] # Step 4-5: 消息传递. out = self.propagate(edge_index, x=x, norm=norm) # Step 6: 添加偏置向量. out = out + self.bias return out -
-
完整GCNs代码
import torch
from torch.nn import Linear, Parameter
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super().__init__(aggr='add') # "Add" aggregation (Step 5).
self.lin = Linear(in_channels, out_channels, bias=False)
self.bias = Parameter(torch.empty(out_channels))
self.reset_parameters()
def reset_parameters(self):
self.lin.reset_parameters()
self.bias.data.zero_()
def forward(self, x, edge_index):
# x has shape [N, in_channels]
# edge_index has shape [2, E]
# Step 1: Add self-loops to the adjacency matrix.
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# Step 2: Linearly transform node feature matrix.
x = self.lin(x)
# Step 3: Compute normalization.
row, col = edge_index
deg = degree(col, x.size(0), dtype=x.dtype)
deg_inv_sqrt = deg.pow(-0.5)
deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
# Step 4-5: Start propagating messages.
out = self.propagate(edge_index, x=x, norm=norm)
# Step 6: Apply a final bias vector.
out = out + self.bias
return out
def message(self, x_j, norm):
# x_j has shape [E, out_channels]
# Step 4: Normalize node features.
return norm.view(-1, 1) * x_j
3.3 边缘卷积
-
公式表达: x i ( k ) = max j ∈ N ( i ) h Θ ( x i ( k − 1 ) , x j ( k − 1 ) − x i ( k − 1 ) ) x_{i}^{(k)} = \max_{j \in \mathcal{N}(i)} h_{\Theta}\left(x_{i}^{(k-1)}, x_{j}^{(k-1)} - x_{i}^{(k-1)}\right) xi(k)=maxj∈N(i)hΘ(xi(k−1),xj(k−1)−xi(k−1))
- 节点特征表示:每个节点 i i i在第 k − 1 k-1 k−1层的特征表示为 x i k − 1 x_i^{k-1} xik−1
- **边缘特征提取:**对于节点 i i i 的每个邻居节点 j j j,计算它们之间的边缘特征。这通常通过计算节点特征的差 x j ( k − 1 ) − x i ( k − 1 ) x_{j}^{(k-1) }- x_{i}^{(k-1)} xj(k−1)−xi(k−1) 来实现,这个差值可以捕捉到节点之间的相对位置或属性差异。
- 边缘卷积操作:使用一个函数 h Θ h_{\Theta} hΘ 来处理节点 i i i的特征和它的邻居节点 j j j的边缘特征。这个函数可以是一个神经网络,参数为 Θ \Theta Θ,它可以学习如何结合这些特征。
- 聚合邻居信息:通过 m a x max max 操作,从所有邻居节点中选择最大的输出值。这个操作可以看作是一种聚合函数,它允许网络关注最重要的邻居节点特征。
- 更新节点特征:最后,将这个最大值作为节点 i i i在第 k k k 层的新特征表示 x i k x_i^{k} xik。
-
代码实现
-
初始化:定义一个简单的 MLP,仅仅有线性层和卷积层
-
消息传递:调用 MessagePassing 库内部的消息传递函数 propagate 用于更新节点属性
-
在 message 中对节点 i i i和节点 i i i的所有邻居节点 j j j进行数据处理
- torch.cat([x_i,x_j-x_i],dim=1):表示将 x_i 和 x_j-x_i 在第一个维度(dim=1)即列上进行拼接。
# 案例 x_i = [[1, 2, 3], [4, 5, 6]] x_j = [[7, 8, 9], [10, 11, 12]] x_j - x_i = [[6, 6, 6], [6, 6, 6]] result = torch.cat(x_i,x_j-x_i,dim=1)#dim=0->行;dim=1->列 print(result) # 输出为:tensor[[1, 2, 3, 6, 6, 6], # [4, 5, 6, 6, 6, 6]] -
重新创建一个DynamicEdgeConv类继承于EdgeConv类,在EdgeConv的基础上增加了动态图构建的功能,在初始化的时候接受一个额外的参数k,用于构建K-NN图。
-
knn_graph(x, self.k, batch, loop=False, flow=self.flow):用于创建一个K-最近邻((K-Nearest Neighbors,简称 K-NN))图,其中K-NN能在经网络的每一层中可以动态地找到每个节点最近的K个邻居节点。这种方法的关键在于它允许网络根据节点的特征在每一层重新定义邻居关系
- 下述为形参
- x (Tensor): 节点特征矩阵,形状为
(N, num_features),其中N是节点的数量,num_features是每个节点特征的维度。 - k (int): 每个节点的最近邻的数量。这是 K-NN 中的 K 值。
- loop (bool, optional): 是否在图中包含自环(即节点连接到自己)。默认为
True。 - dim (int, optional): 用于计算距离的特征维度。如果特征矩阵是多维的,这可以指定使用哪一维来计算距离。
- batch (LongTensor, optional): 用于批处理的节点索引,形状为
(N,)。如果提供,它应该包含每个节点所属批次的索引。 - flow (string, optional): 指定边的方向。可以是
'source_to_target'或'target_to_source'。如果设置为'source_to_target',则边从源节点指向目标节点;如果设置为'target_to_source',则相反。 - dist (Tensor, optional): 预先计算好的距离矩阵。如果提供,将使用这个矩阵而不是重新计算。
- y (Tensor, optional): 用于加速 K-NN 搜索的辅助张量,例如,可以是节点的聚类标签。
- **Algorithm (optional): 指定用于 K-NN 搜索的算法。可以是
'bruteforce'或'balltree'。 - num_workers (int, optional): 用于加载数据的子进程数量。
-
-
完整代码:
import torch from torch.nn import Sequential as Seq, Linear, ReLU, BatchNorm1d, Dropout from torch_geometric.nn import MessagePassing from torch_geometric.nn import knn_graph class EdgeConv(MessagePassing): def __init__(self,in_channels, out_channels): super(EdgeConv, self).__init__(aggr='max') # "Max" aggregation. self.mlp = Seq(Linear(2 * in_channels, out_channels), ReLU(), Linear(out_channels,out_channels)) def forward(self, x, edge_index): return self.propagate(edge_index, x=x) def message(self, x_i, x_j): # tmp为一个[E,2*in_channels]的节点特征 # 因为在tmp中即考虑了节点i的节点特征,同时也考虑了节点i和节点j之间的特征差异,故节点特征数为2*in_channls tmp=torch.cat([x_i,x_j-x_i],dim=1) return self.mlp(tmp) # tmp经过mlp后得到[E,out_channels]的特征 # DynamicEdgeConv继承于EdgeConv类 class DynamicEdgeConv(EdgeConv): def __init__(self,in_channels, out_channels, k=6): super().__init__(in_channels, out_channels) self.k = k def forward(self, x, batch=None): edge_index = knn_graph(x, self.k, batch, loop=False, flow=self.flow) return super().forward(x, edge_index)
总结:
这里主要介绍了图卷积神经网络的公式是如何推导得到到,同时介绍如何从公式到具体代码实现。下一篇文章将会基于本篇文章中的图卷积神经网络,讲述该图卷积神经网络的应用。























 1086
1086

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








