02 Regression & Classification
Regression
- 股票价格预测:
- f(一些信息) = 明天的道琼斯指数
- 自动驾驶:
- f(雷达输入) = 方向盘&油门
- 推荐系统:
- f(使用者A, 商品B) = 购买的可能性
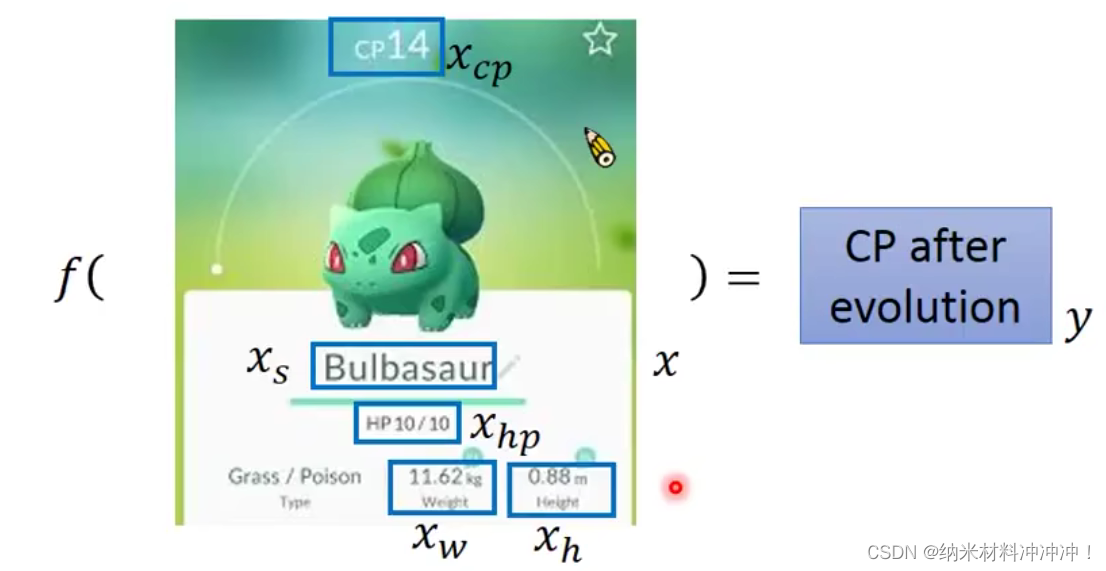
- 预测宝可梦的战斗力(Combat Power)
- f(某一只宝可梦) = 进化后的CP值
- 即 f ( x ) = y f(x) = y f(x)=y
- 其中x为一个向量 :
- x c p = 进化前 c p 值 x_{cp} = 进化前cp值 xcp=进化前cp值
- x h p = 进化前生命值 x_{hp} = 进化前生命值 xhp=进化前生命值
- x s = 宝可梦名字 x_{s} = 宝可梦名字 xs=宝可梦名字
- x w = 宝可梦体重 x_{w} = 宝可梦体重 xw=宝可梦体重
- x h = 宝可梦身高 x_{h} = 宝可梦身高 xh=宝可梦身高
1. 指定一个Model
y
=
b
+
w
∗
x
c
p
y = b+w*x_{cp}
y=b+w∗xcp
上面这个function是一个线性模型,Linear model
y
=
b
+
∑
w
i
∗
x
i
y = b + \sum w_i*x_i
y=b+∑wi∗xi
我们称
w
i
w_i
wi 为weight,
b
b
b为bias,
x
i
x_i
xi为feature
假设我们只用
x
c
p
x_{cp}
xcp作为输入
2. 训练模型
训练集: 10只宝可梦的进化前信息与进化后的cp值: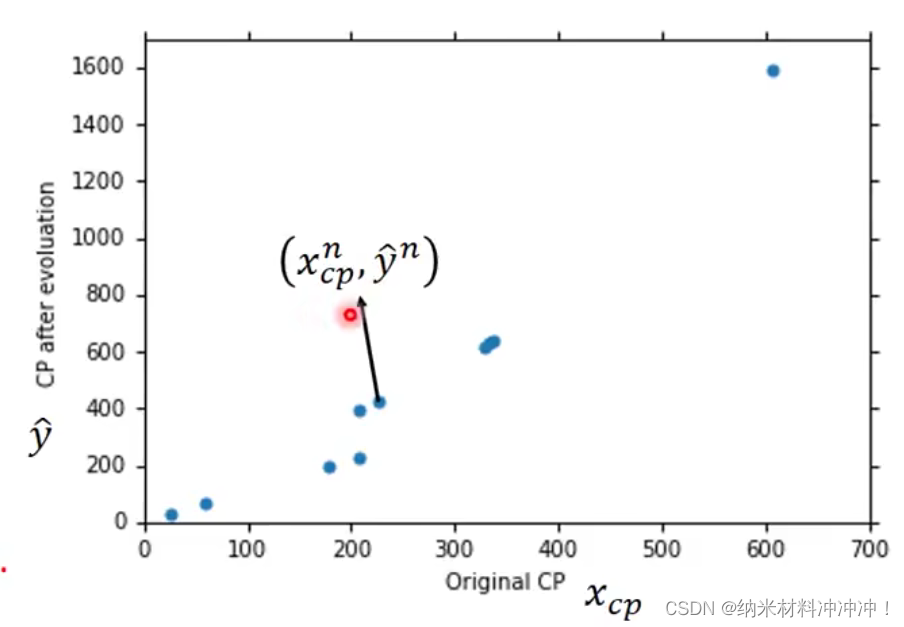
定义一个function的好坏
Loss function:输出一个function的坏的程度
L
(
f
)
=
L
(
w
,
b
)
L(f) = L(w,b)
L(f)=L(w,b)
衡量一组b和w的好坏,在此: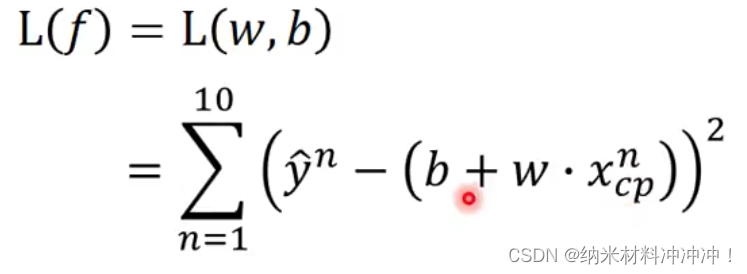
Σ
(
真实数值
−
预测数值
)
2
\Sigma(真实数值-预测数值)^2
Σ(真实数值−预测数值)2
3. 找到最好的function
找到一个w与b的参数,使得Loss function的值最小
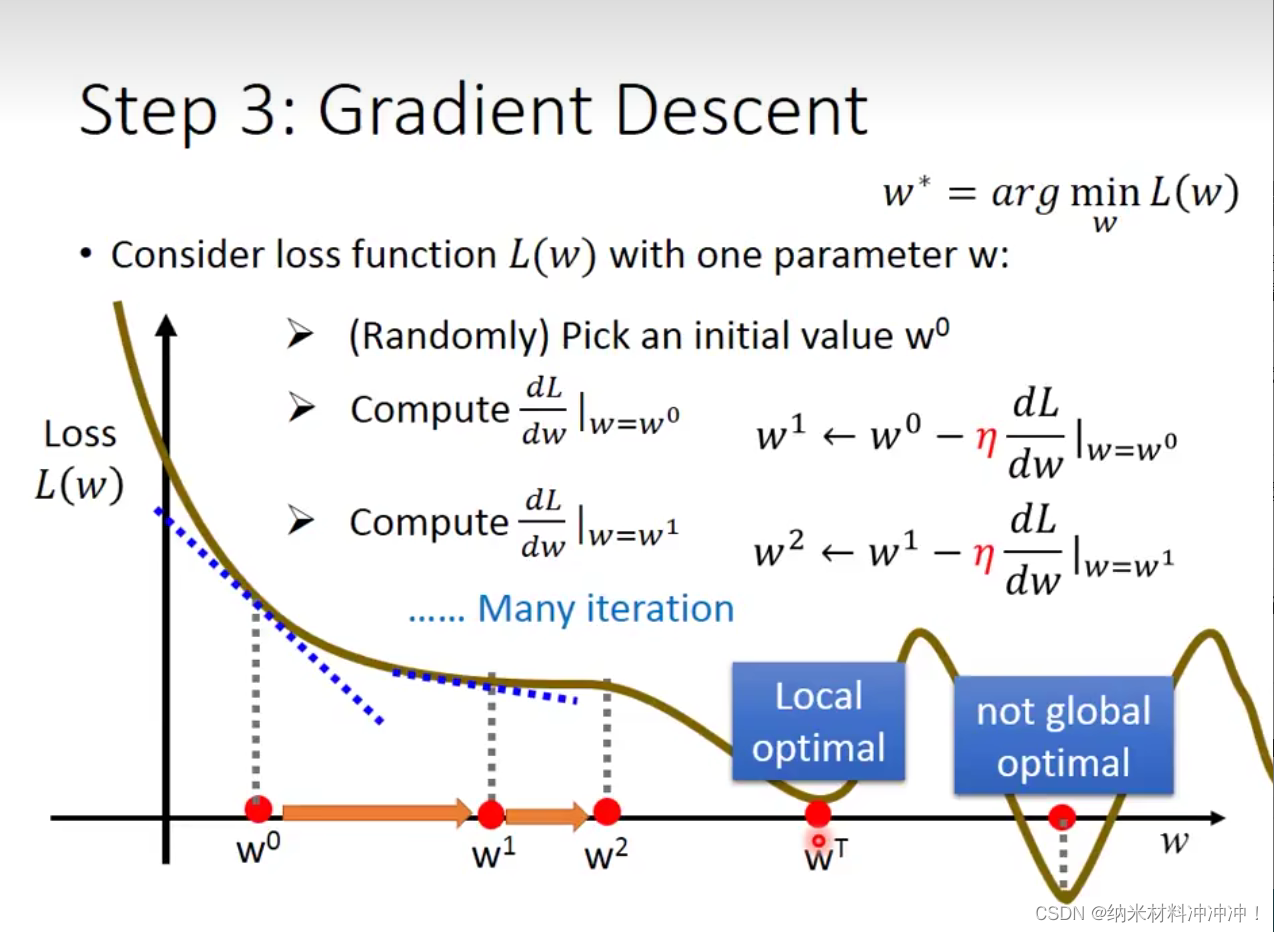
Gradient Descent
- 随机选取一个 w 0 w^0 w0
- 计算 d L d w ∣ w = w 0 \frac{dL}{dw}|_{w=w^0} dwdL∣w=w0
- η \eta η称为学习率,在 w 0 w^0 w0应该更新 η d L d W ∣ w = w 0 \eta \frac{dL}{dW}|_{w=w^0} ηdWdL∣w=w0 即 w 1 = w 0 − η d L d W ∣ w = w 0 w^1 = w^0 - \eta \frac{dL}{dW}|_{w=w^0} w1=w0−ηdWdL∣w=w0
- 重复上述步骤
对于两个参数也是一样,只不过初始时随机指定两个数 w 0 , b 0 w^0, b^0 w0,b0,然后用偏微分代替导数
问题:很多时候我们的LossFunction是不规则的,有事会陷入局部最优而无法获得全局最优,这取决于LossFunction是否为convex
- convex:如果一个函数没有local optimal,则称这个函数为convex的(对于任何的初始值,我们总可以找到全局最优!)
初始Model的选取十分有讲究:
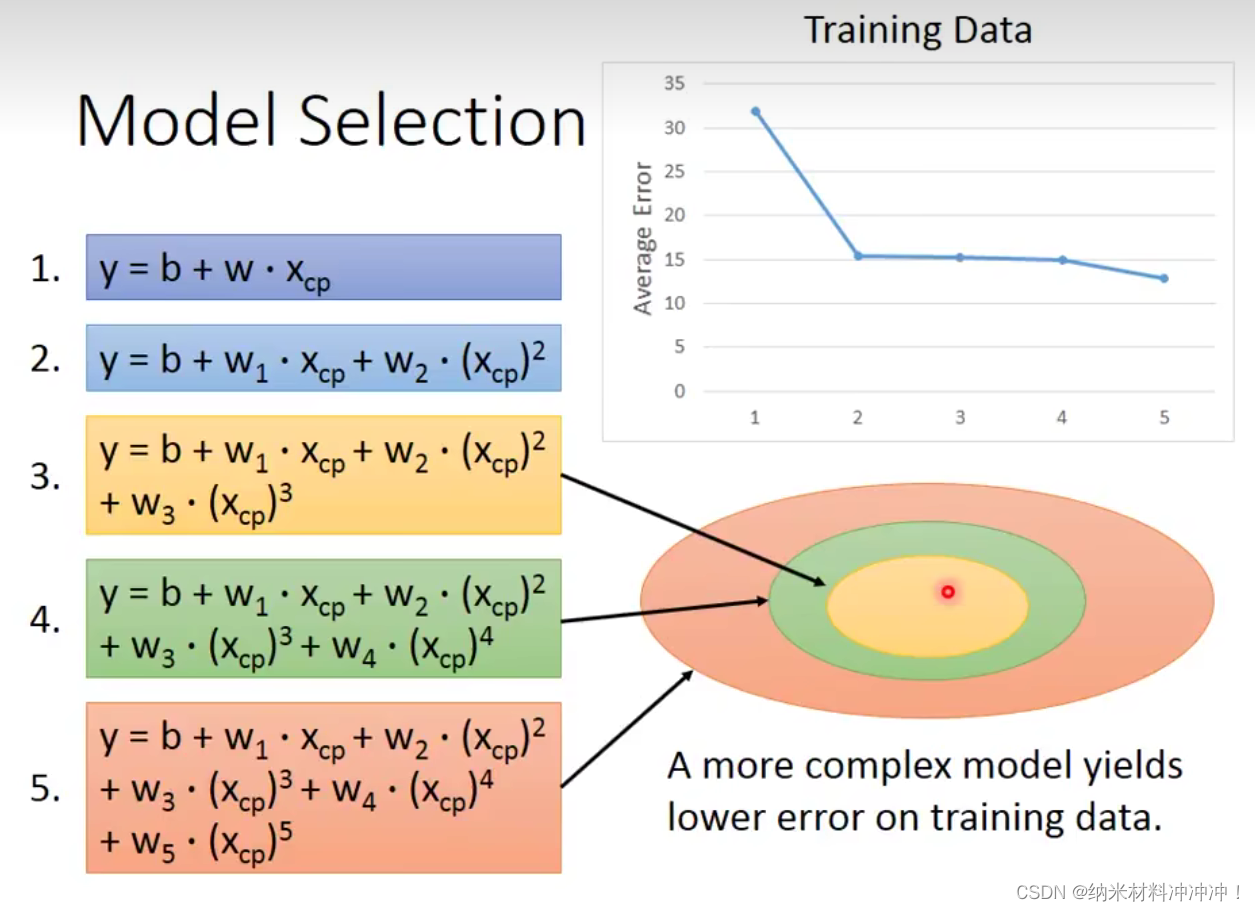
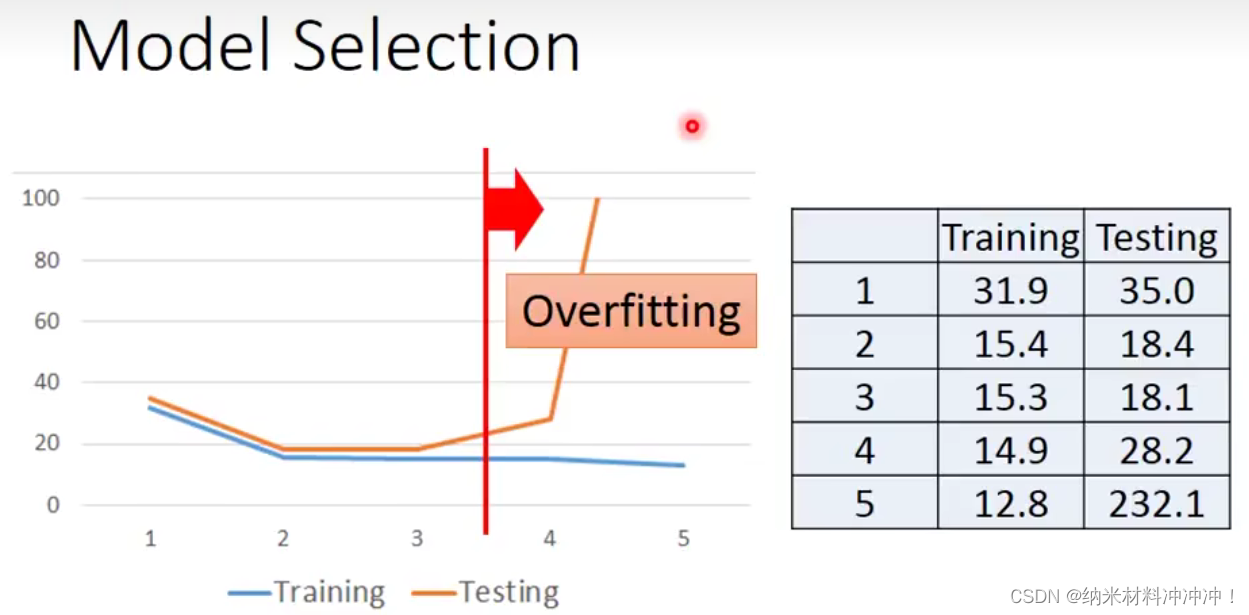
我们选择一个function,在Training Data上表现很好的function可能Testing Data上的表现并不好(过拟合Overfitting)
现实世界中Model并不如此简单:
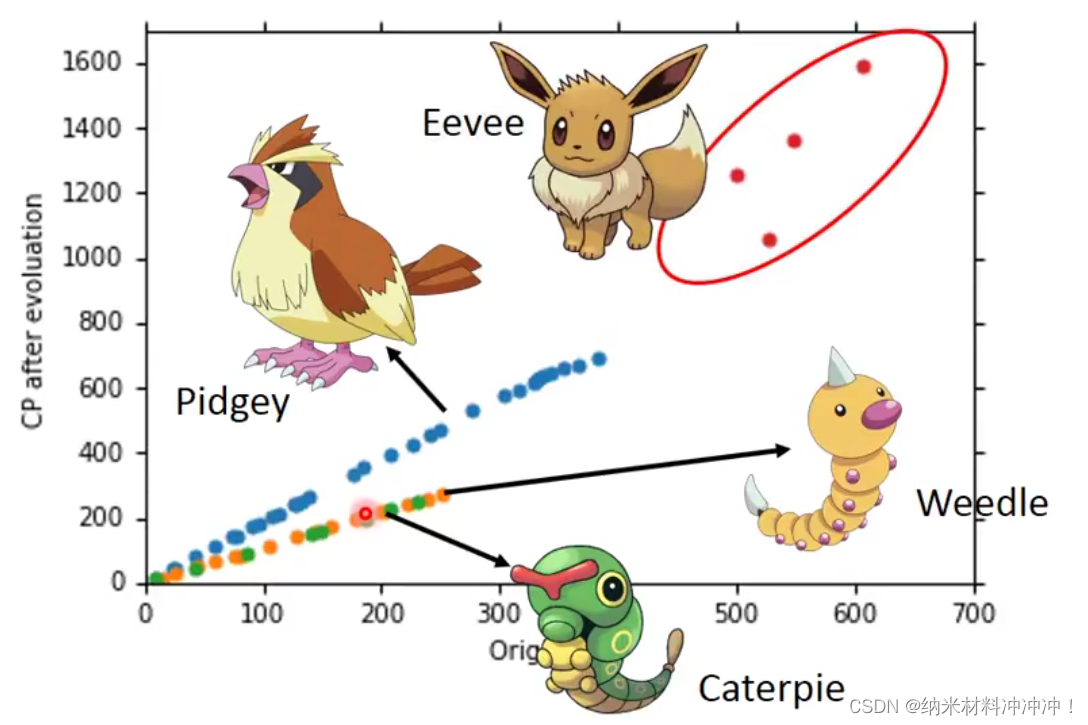
我们发现不同的物种有不同的function,对于不同的物种我们选择对应的function
发现还是可以用一个Linear Model表示:
其中
δ
(
x
)
\delta(x)
δ(x)取值为1或0

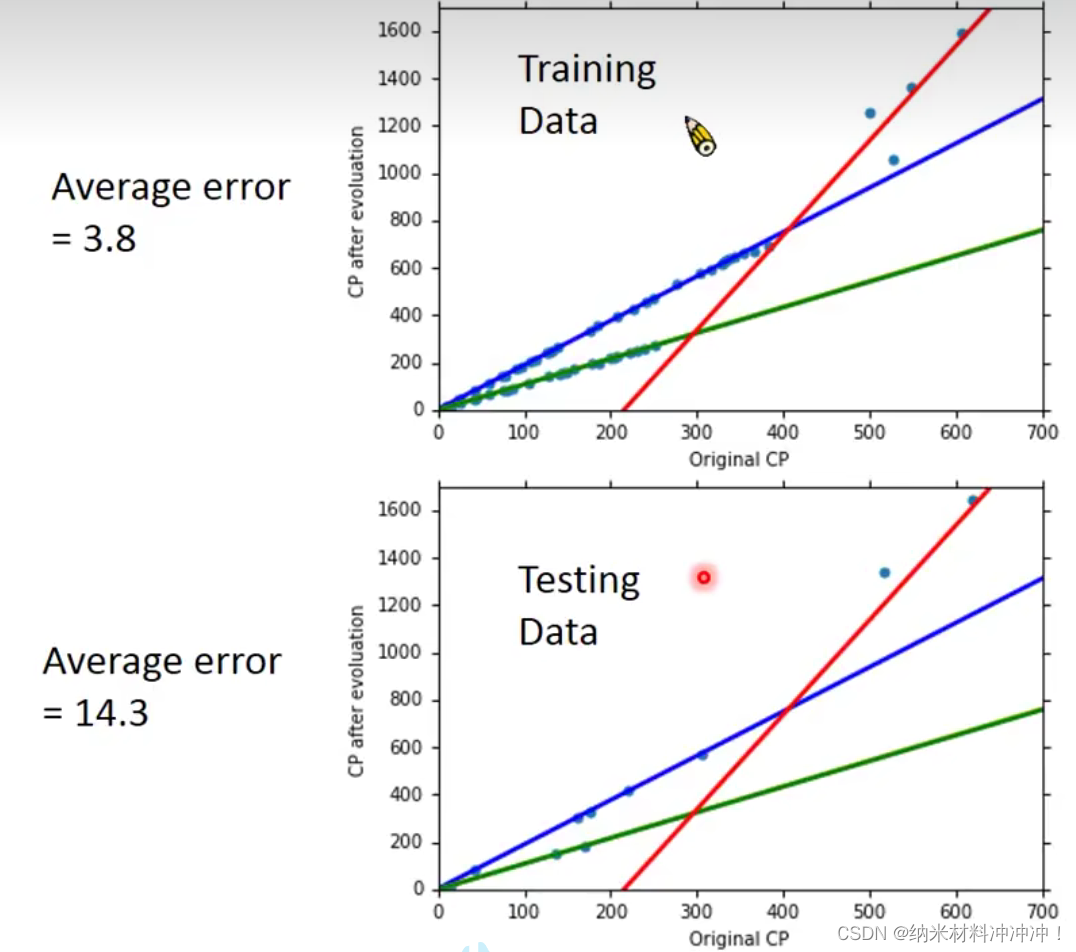
如此我们获得了更好的预测模型:
4. 避免过拟合
删除一些“关系不大”的参数
常常需要背景知识
正则化
使用正则化:为避免过拟合overfitting,我们期望参数值更接近0(更平滑,对于输入更不敏感!)
- model: y = b + ∑ w i ∗ x i y = b + \sum w_i*x_i y=b+∑wi∗xi
- 对于一个输入的变化量 Δ x i \Delta x_i Δxi,如果有更平滑的model,即 w i w_i wi的取值更小,我们得到的 Δ y i \Delta y_i Δyi 受到的影响更小
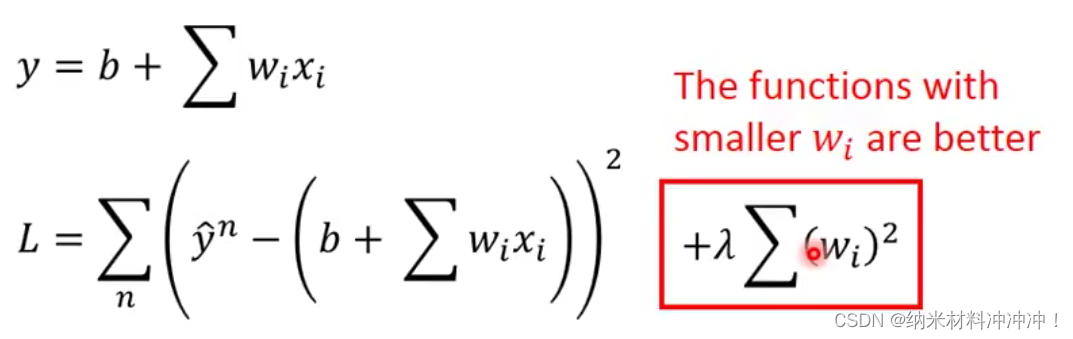
- 正则项并不需要加入 b b b的值
但是model也不能太smooth,否则training与testing的结果会更差,因此我们需要使用 λ \lambda λ来调整
Classification
- 金融信誉评估
- 输入收入、存款、学历等,输出金融信用分数
- 医疗诊断
- 输入当前症状,年龄,性别等,输出可能的病
- 人脸识别
- 输入人脸,输出人名
- 宝可梦应用!
- 输入宝可梦的参数,输出宝可梦属性

如何将一只宝可梦作为函数的输入?
- 输入宝可梦的参数,输出宝可梦属性
- 所有维度的参数作为一个向量
经过Regression的学习,我们甚至可以直接用Regression的方式进行这样的研究:(二分类)
- 如果 f ( x ) > 0 f(x) > 0 f(x)>0,就是class 1
- 如果
f
(
x
)
<
0
f(x) < 0
f(x)<0,就是class 2
如下左图: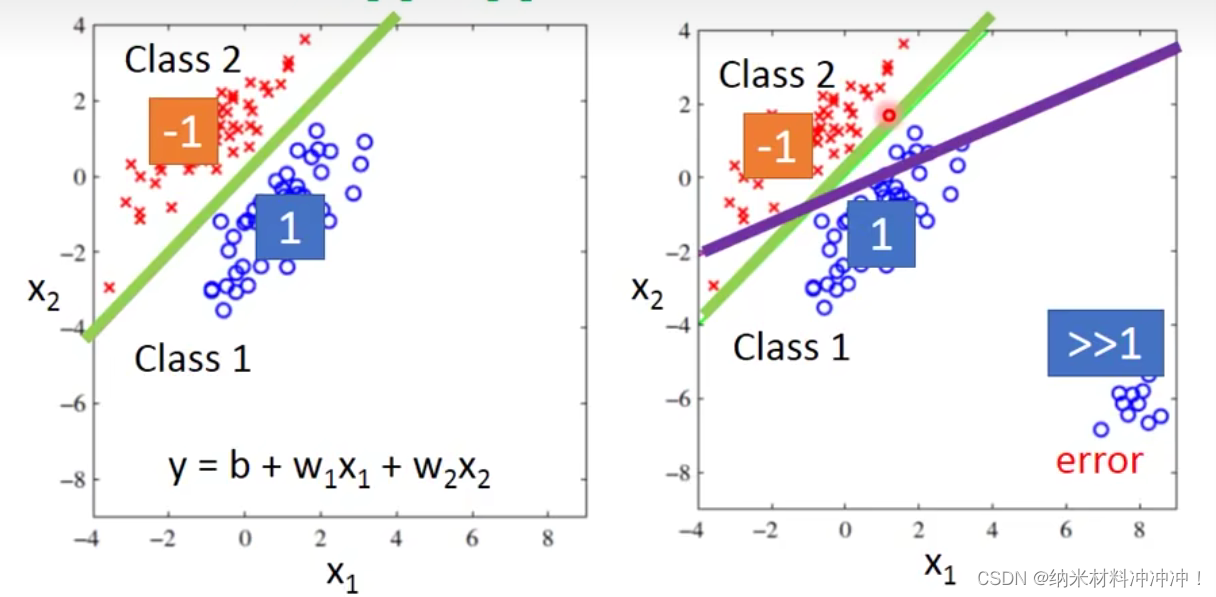
问题:对于Regression与classification问题,model好坏的评判标准不同。 - Regression会惩罚那些过于“正确”的结果
应该怎么做?
- 提出一个Function,Model
- 在我们的model
f
(
x
)
f(x)
f(x)中包含另一个函数
g
(
x
)
g(x)
g(x),
f
(
x
)
f(x)
f(x)的取值取决于
g
(
x
)
g(x)
g(x)的正负
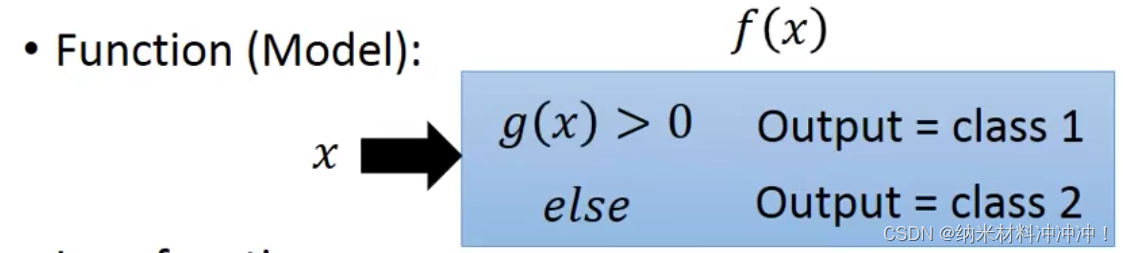
- 在我们的model
f
(
x
)
f(x)
f(x)中包含另一个函数
g
(
x
)
g(x)
g(x),
f
(
x
)
f(x)
f(x)的取值取决于
g
(
x
)
g(x)
g(x)的正负
- 定义损失函数 Loss function
- 我们显然不能使用Regression那样的Lossfunction,因为他会惩罚过于正确的分类结果
- 我们需要让model分类错误的样本个数最小!

- 得到正确的function
- 例如可以使用Preceptron,SVM等(日后会讲)
现有两个盒子(Generative Model)
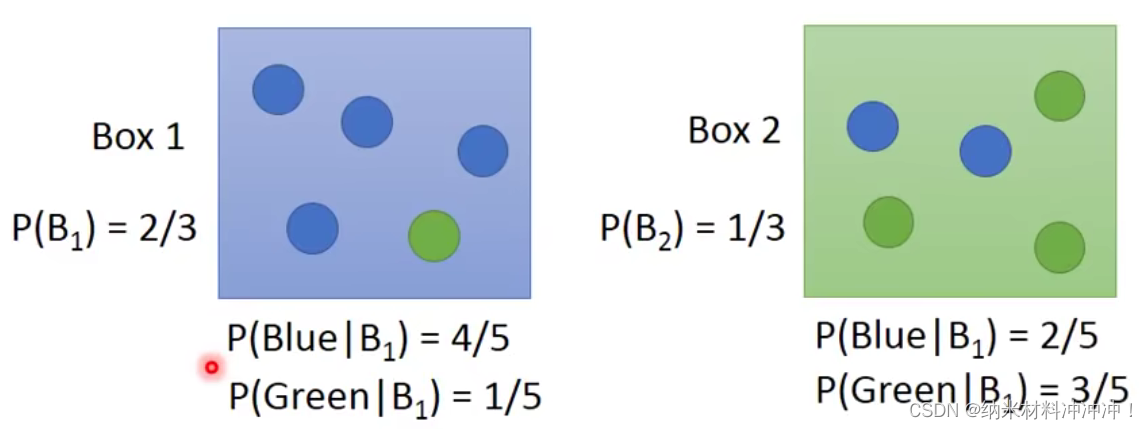
已知我们抽到了一个蓝色球,来自两个盒子的概率分别为多少?
根据贝叶斯定理:
-
P ( C 1 ∣ B ) = P ( C 1 , B ) P ( B ) = P ( B ∣ C 1 ) P ( C 1 ) P ( B ∣ C 1 ) P ( C 1 ) + P ( B ∣ C 2 ) P ( C 2 ) P(C_1|B) = \frac {P(C_1, B)}{P(B)} = \frac {P(B|C_1)P(C_1)}{P(B|C_1)P(C_1) + P(B|C_2)P(C_2)} P(C1∣B)=P(B)P(C1,B)=P(B∣C1)P(C1)+P(B∣C2)P(C2)P(B∣C1)P(C1)
-
P ( C 2 ∣ B ) = P ( C 2 , B ) P ( B ) = P ( B ∣ C 2 ) P ( C 2 ) P ( B ∣ C 1 ) P ( C 1 ) + P ( B ∣ C 2 ) P ( C 2 ) P(C_2|B) = \frac {P(C_2, B)}{P(B)} = \frac {P(B|C_2)P(C_2)}{P(B|C_1)P(C_1) + P(B|C_2)P(C_2)} P(C2∣B)=P(B)P(C2,B)=P(B∣C1)P(C1)+P(B∣C2)P(C2)P(B∣C2)P(C2)
这样一个分类问题就变为概率问题:
我们只要知道
P
(
x
∣
C
1
)
P(x|C_1)
P(x∣C1)与
P
(
x
∣
C
2
)
P(x|C_2)
P(x∣C2)的概率,几率最大的case,就是我们的分类结果!
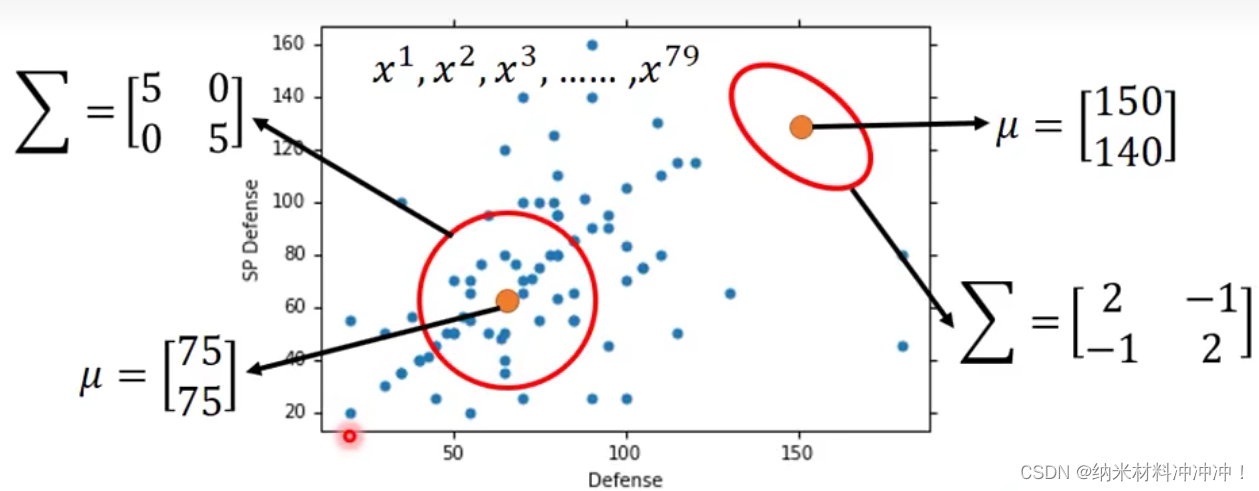
已知79只水系和61只一般系宝可梦的数据,现有一个未知宝可梦海龟,该如何确定海龟属于哪一类?
- 解决这个分类问题,只需要知道 P ( w a t e r ∣ 海龟 ) P(water|海龟) P(water∣海龟)与 P ( n o r m a l ∣ 海龟 ) P(normal|海龟) P(normal∣海龟)哪个更大即可!
- 显然我们可以得到 P ( w a t e r ) P(water) P(water)与 P ( n o r m a l ) P(normal) P(normal)
- 但是我们该如何计算 P ( 海龟 ∣ w a t e r ) P(海龟|water) P(海龟∣water)与 P ( 海龟 ∣ n o r m a l ) P(海龟|normal) P(海龟∣normal)?
- 我们假设79个水系神奇宝贝的分布来自Gaussian Distribution
- 对于不同的均值
μ
\mu
μ与协方差矩阵
Σ
\Sigma
Σ,我们可以得到某个x被sample出的概率
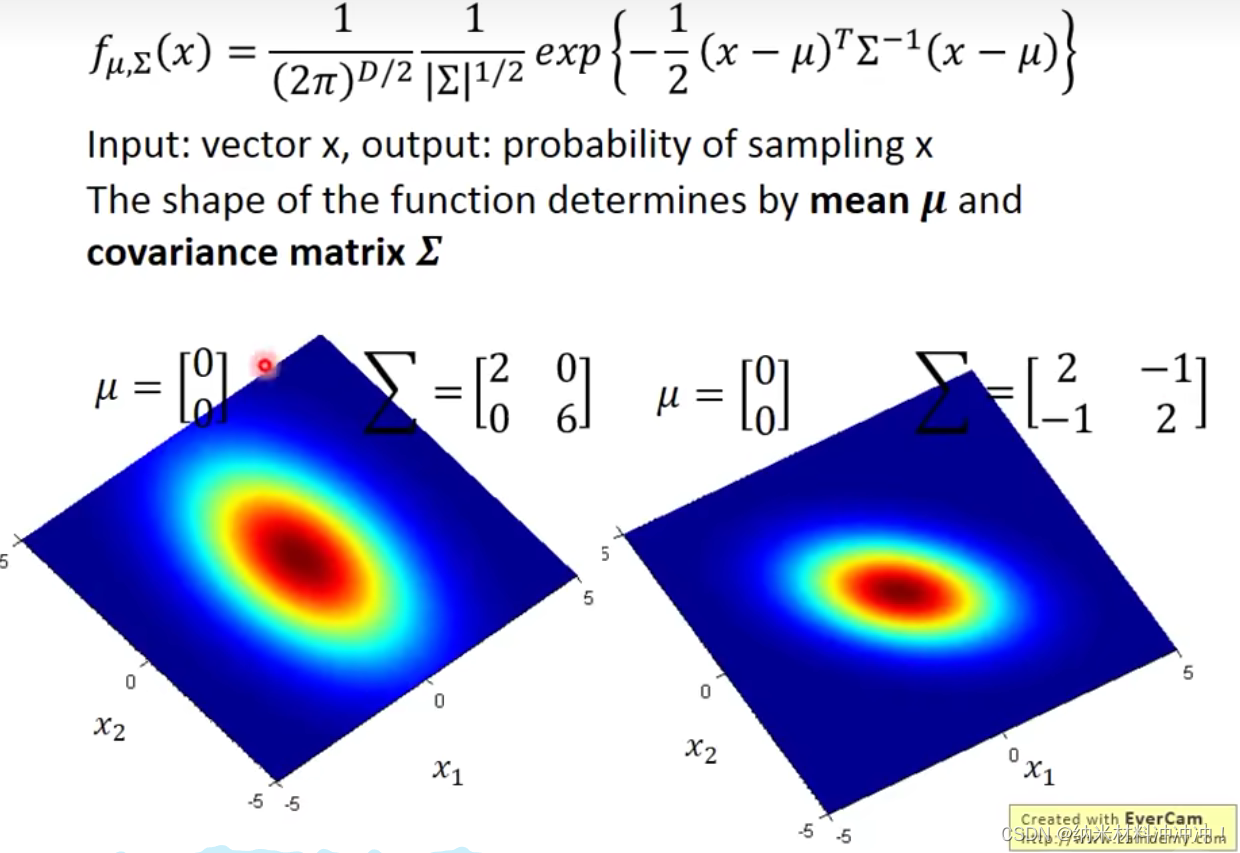
- 最大似然估计:显然任何一个Gaussian分布都可以sample出这79个点,但几率并不一样大
- 从Guassian分布中sample出上面79个点的几率为: L ( μ , Σ ) = f μ , Σ ( x 1 ) ∗ f μ , Σ ( x … … 2 ) . . . . . . ∗ f μ , Σ ( x 79 ) L(\mu, \Sigma) = f_{\mu, \Sigma}(x^1) * f_{\mu, \Sigma}(x……2) ...... * f_{\mu, \Sigma}(x^{79}) L(μ,Σ)=fμ,Σ(x1)∗fμ,Σ(x……2)......∗fμ,Σ(x79)
- 穷举不同的
μ
,
Σ
\mu, \Sigma
μ,Σ,得到可以让
L
(
μ
,
Σ
)
L(\mu, \Sigma)
L(μ,Σ)最大的
μ
∗
,
Σ
∗
\mu^*, \Sigma^*
μ∗,Σ∗,我们就有了真正的
G
(
μ
c
,
Σ
c
)
G(\mu ^c, \Sigma ^c)
G(μc,Σc)
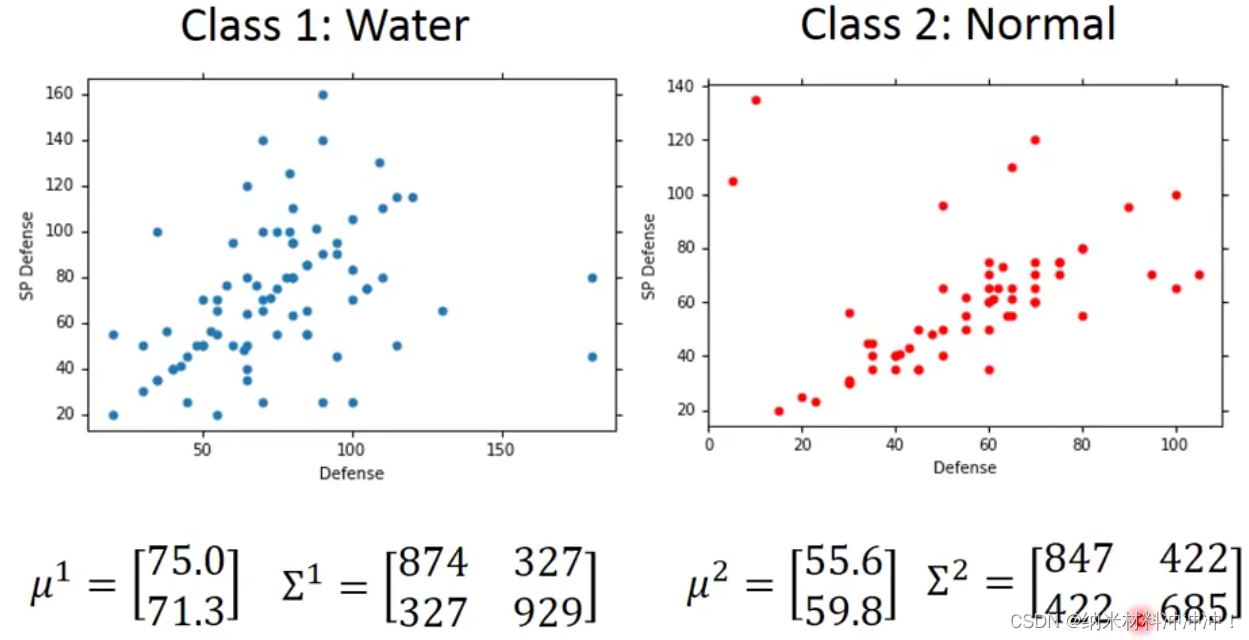 - 于是我们可以计算:
P
(
海龟
∣
w
a
t
e
r
)
P(海龟|water)
P(海龟∣water)与
P
(
海龟
∣
n
o
r
m
a
l
)
P(海龟|normal)
P(海龟∣normal)
- 于是我们可以计算:
P
(
海龟
∣
w
a
t
e
r
)
P(海龟|water)
P(海龟∣water)与
P
(
海龟
∣
n
o
r
m
a
l
)
P(海龟|normal)
P(海龟∣normal)
一般来说我们使用最大似然估计的Gaussian Function中
Σ
\Sigma
Σ取值相同,因此Loss Function有:
L
(
μ
1
,
μ
2
,
Σ
)
=
[
f
μ
1
,
Σ
(
x
1
)
∗
f
μ
1
,
Σ
(
x
2
)
∗
.
.
.
∗
f
μ
1
,
Σ
(
x
79
)
]
∗
[
f
μ
2
,
Σ
(
x
80
)
∗
f
μ
2
,
Σ
(
x
81
)
∗
.
.
.
∗
f
μ
2
,
Σ
(
x
140
)
]
L(\mu^1, \mu^2, \Sigma) = [ f_{\mu^1, \Sigma}(x^1)*f_{\mu^1, \Sigma}(x^2)*...*f_{\mu^1, \Sigma}(x^{79}) ] * [ f_{\mu^2, \Sigma}(x^{80})*f_{\mu^2, \Sigma}(x^{81})*...*f_{\mu^2, \Sigma}(x^{140})]
L(μ1,μ2,Σ)=[fμ1,Σ(x1)∗fμ1,Σ(x2)∗...∗fμ1,Σ(x79)]∗[fμ2,Σ(x80)∗fμ2,Σ(x81)∗...∗fμ2,Σ(x140)]

如何选择Probability Distribution?
- 在本例中我们使用Gaussian Distribution
- 二分类问题中可能会使用Bernoulli Distribution
- 如果输入的各个特征独立我们可以选用Naive Bayes Distribution
后验概率 Posterior Probability
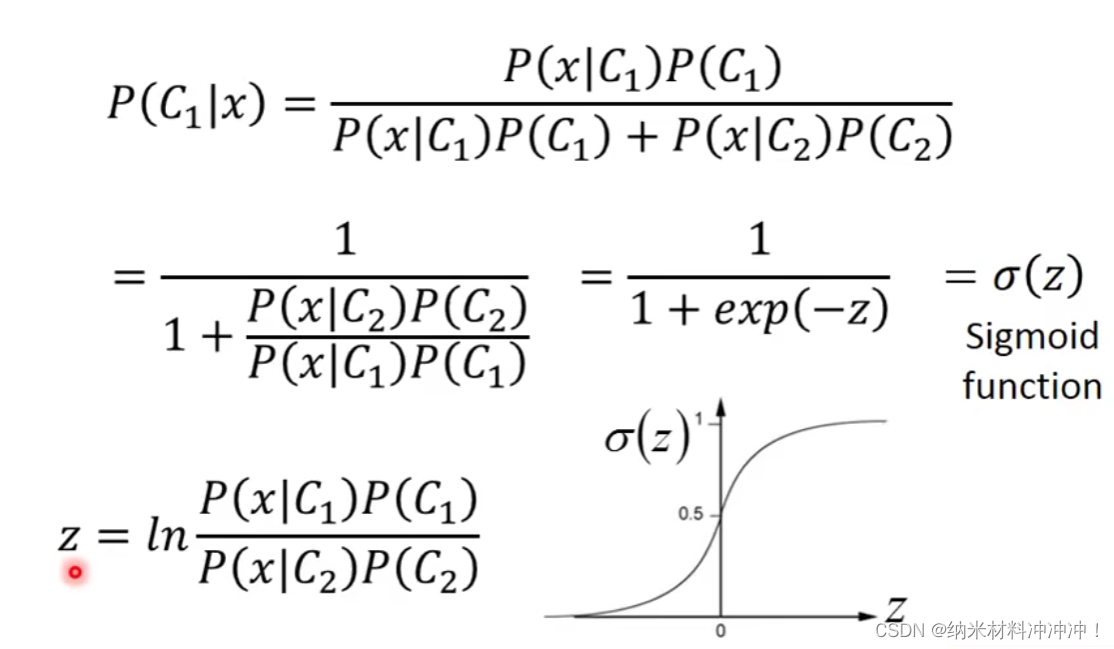
一般我们会假设分布的
Σ
\Sigma
Σ是共用的,经过推导得:

发现:
z
=
w
T
∗
x
+
b
z = w^T * x + b
z=wT∗x+b
因此后验概率:
P
(
C
1
∣
x
)
=
σ
(
w
T
∗
x
+
b
)
P(C_1|x) = \sigma(w^T * x + b)
P(C1∣x)=σ(wT∗x+b)
Logistic Regression
上节中我们发现
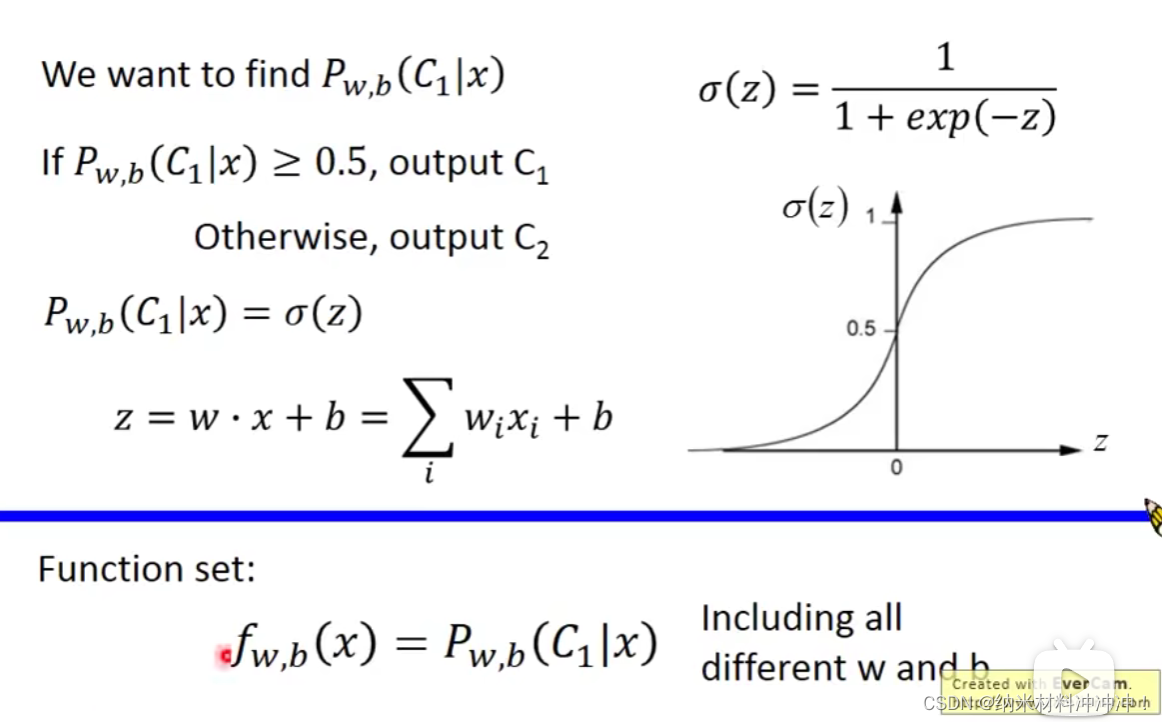
并不需要先根据分类结果
L
(
μ
,
Σ
)
L(\mu, \Sigma)
L(μ,Σ)模拟出一个
G
a
u
s
s
i
a
n
D
i
s
t
r
i
b
u
t
i
o
n
Gaussian Distribution
GaussianDistribution再计算,可以直接通过w与b得到一个后验概率
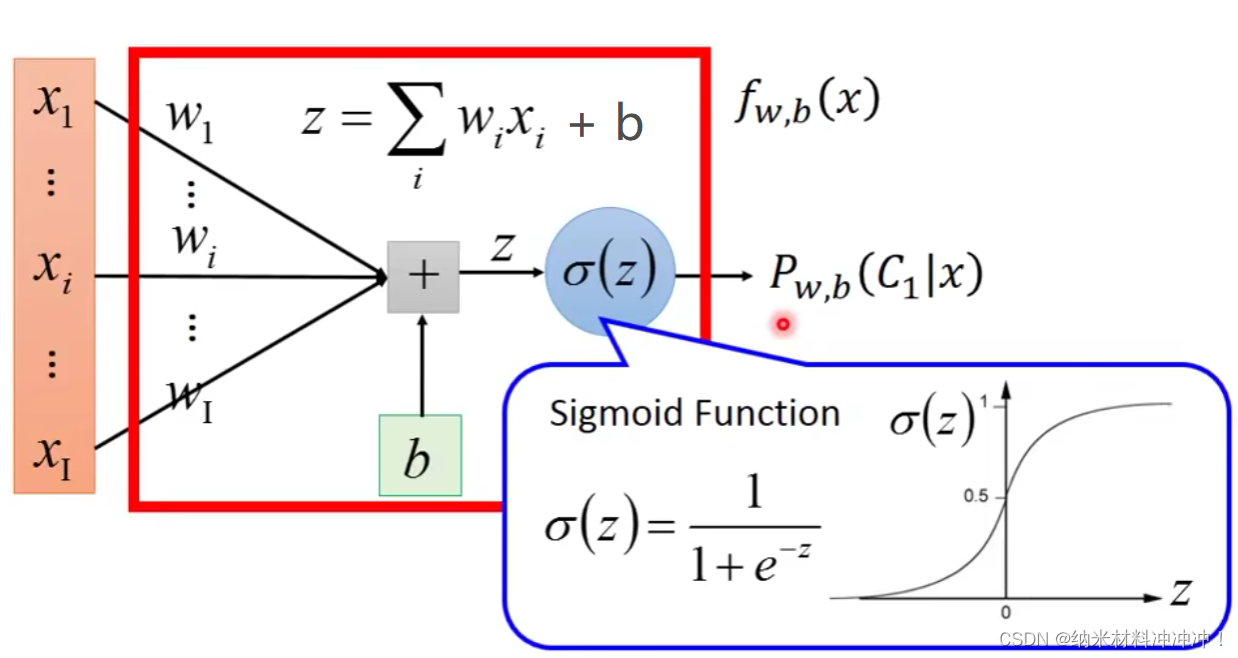
比较Logistic Regression与Linear Regression:

黑色为交叉熵,红色为平方:
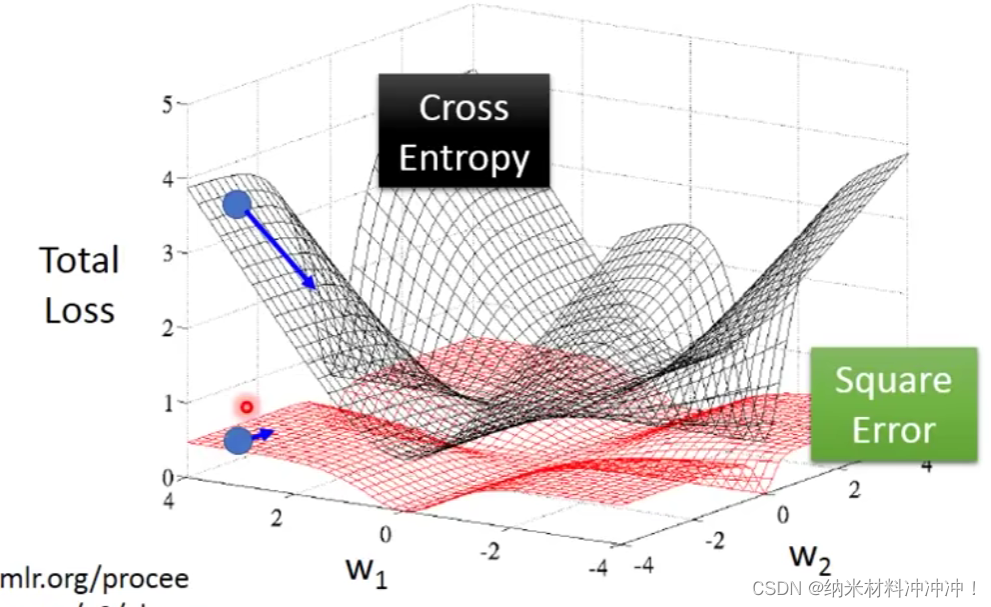
- 距离目标很近时:Square Error与Cross Entropy均有很低的微分值
- 距离目标很远时:Cross entroy的微分值很大,而Square Error的微分值也很低!
- 因此:如果使用square error并制定了一个很远的随机起点,就会导致参数更新很慢甚至不更新的情况






















 3万+
3万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








