LeetCode 热题 100—— 将有序数组转换为二叉搜索树(二叉树）+ 验证二叉搜索树（二叉树）

目录

108. 将有序数组转换为二叉搜索树 简单

98. 验证二叉搜索树 中等

---

简单

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。

示例 1：

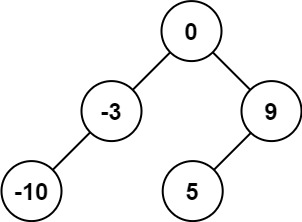
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

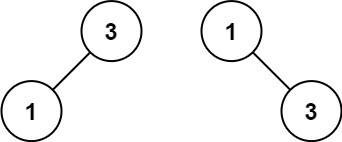
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• 1 <= nums.length <= 104

• -104 <= nums[i] <= 104

• nums 按 严格递增 顺序排列

核心思路

1. 二叉搜索树（BST）特性：左子树所有节点值 < 根节点值 < 右子树所有节点值。

2. 高度平衡要求：左右子树的高度差不超过 1。

3. 有序数组的特性：选择中间元素作为根节点，可自然满足 BST 特性并保持平衡。

//方法一：中序遍历，总是选择中间位置左边的数字作为根节点
​
//时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
//空间复杂度：O(logn)，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是 O(logn)。
​
​
​
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }
​
    TreeNode* helper(vector<int>& nums, int left, int right) {
        // 终止条件：当左边界大于右边界时，返回空节点
        if (left > right) {
            return nullptr;
        }
​
        // 总是选择中间位置左边的数字作为根节点
        int mid = (left + right) / 2;
​
        // 创建根节点并递归构建左右子树
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;
    }
};

//方法二：中序遍历，总是选择中间位置右边的数字作为根节点
​
//时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
//空间复杂度：O(logn)，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是 O(logn)。
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }
​
    TreeNode* helper(vector<int>& nums, int left, int right) {
        if (left > right) {
            return nullptr;
        }
​
        // 总是选择中间位置右边的数字作为根节点
        int mid = (left + right + 1) / 2;
​
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;
    }
};
​

//方法三：中序遍历，选择任意一个中间位置数字作为根节点
​
//时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
//空间复杂度：O(logn)，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是 O(logn)。
​
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }
​
    TreeNode* helper(vector<int>& nums, int left, int right) {
        if (left > right) {
            return nullptr;
        }
​
        // 选择任意一个中间位置数字作为根节点
        //rand() % 2 会随机生成 0 或 1，相当于给原中间索引增加一个随机偏移量。
        int mid = (left + right + rand() % 2) / 2;
​
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;
    }
};

98. 验证二叉搜索树 中等

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。

• 节点的右子树只包含 大于 当前节点的数。

• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

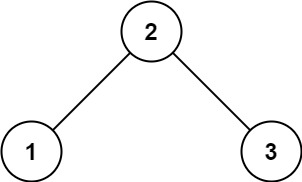
输入：root = [2,1,3]
输出：true

示例 2：

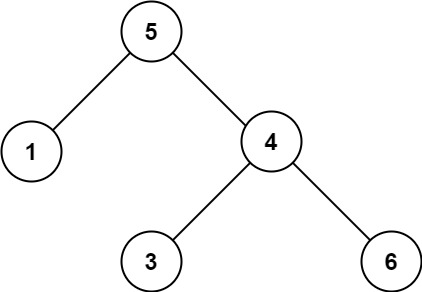
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内

• -231 <= Node.val <= 231 - 1

//方法一: 递归
​
//时间复杂度：O(n)，其中 n 为二叉树的节点个数。在递归调用的时候二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。
//空间复杂度：O(n)，其中 n 为二叉树的节点个数。递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，即二叉树的高度。最坏情况下二叉树为一条链，树的高度为 n ，递归最深达到 n 层，故最坏情况下空间复杂度为 O(n)
​
class Solution {
public:
    // 辅助函数：验证以 root 为根的子树是否满足 (lower, upper) 的范围约束
    bool helper(TreeNode* root, long long lower, long long upper) {
        // 空树是有效的 BST
        if (root == nullptr) {
            return true;
        }
        // 检查当前节点的值是否超出范围
        if (root -> val <= lower || root -> val >= upper) {
            return false;
        }
        // 递归验证左子树和右子树
        // 左子树的上界是当前节点的值
        // 右子树的下界是当前节点的值
        return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
    }
     // 主函数：从根节点开始验证，初始上下界为无限小和无限大
    bool isValidBST(TreeNode* root) {
        //使用 LONG_MIN 和 LONG_MAX（long long 类型的最小值和最大值）避免溢出问题。
        return helper(root, LONG_MIN, LONG_MAX);
    }
};

//方法二：中序遍历
​
/*
核心思路
BST 的中序遍历特性：中序遍历（左→根→右）BST 会得到一个严格递增的节点值序列。因此，只需检查中序遍历过程中每个节点的值是否严格大于前一个节点的值即可。
迭代实现中序遍历：使用栈模拟递归调用，避免递归带来的栈溢出风险，同时在遍历过程中实时比较当前节点值与前一个值的大小关系。
*/
​
//时间复杂度：O(n)，其中 n 为二叉树的节点个数。二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。
//空间复杂度：O(n)，其中 n 为二叉树的节点个数。栈最多存储 n 个节点，因此需要额外的 O(n) 的空间。
​
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> stack;
        // 初始值设为 INT_MIN-1，避免边界问题
        //INT_MIN 是 C++ 标准库中的一个宏，表示 int 类型的最小值。
        long long inorder = (long long)INT_MIN - 1;
​
        while (!stack.empty() || root != nullptr) {
            // 1. 遍历左子树，将所有左节点压入栈
            while (root != nullptr) {
                stack.push(root);
                root = root -> left;
            }
            
            // 2. 弹出栈顶节点（当前最左节点）
            root = stack.top();
            stack.pop();
            
            // 3. 检查当前节点值是否大于前一个值
            if (root -> val <= inorder) {
                // 若不满足递增条件，直接返回 false
                return false;
            }
            
            // 更新前一个值为当前节点值
            inorder = root -> val;
            
            // 4. 转向右子树
            root = root -> right;
        }
        // 所有节点检查完毕，满足 BST 条件
        return true;
    }
};