有限元法计算二维圆柱绕流问题——无粘有环量的情况

百宝袋里是数学和代码

已于 2023-07-12 10:01:22 修改

阅读量1k

点赞数 1

分类专栏：计算流体力学文章标签： python 算法

于 2023-06-29 05:12:46 首次发布

本文链接：https://blog.csdn.net/weixin_52046577/article/details/131435301

版权

计算流体力学专栏收录该内容

4 篇文章 0 订阅

订阅专栏

写在前面

该系列文章是笔者的学习记录，旨在通过分享促进交流加深理解，文中难免有许多纰漏与理解不当之处，若能批评指正必定感激不尽。

侧重分享经典CFD方法的具体实现结果，详细的理论推导请参考教材。

一、问题描述

与上一篇有限元法计算二维圆柱绕流问题——Python代码实现不同的是，本文考虑有环量圆柱绕流问题的求解，这同样是一个有精确解的问题。加入了平面点涡流动以后，圆柱绕流问题表现出更贴近现实的升力的现象。

取一个充分大的区间，在外边界提无穷远边界条件。下面将逐步讲解用有限元法计算的过程，并针对数值结果考察外边界距离以及网格尺度对误差的影响。

回顾-有限元法简介：

有限元法是求解计算力学问题的重要方法。首先需要将求解区域进行离散化，划分为许多几何形状简单规则的单元，如二维的三角形或四边形，三维的四面体或六面体；然后，在每个单元内，用一个比较简单的解析函数来逼近微分方程的解，此函数在单元内用一组选定的单元基函数的线性组合表示，而其中的系数通常是节点上的物理量，它是待求解的。这样，每个单元只要有适当数量的节点物理量的值，就可以满足对插值函数的光滑性和精度的要求；接下来，在满足微分方程和相应的初边值条件下，对全部子域进行积分：对每个单元分别进行积分，形成“单元方程”，通过总体合成，得到总体有限元方程组；最后，用适当的方法解方程组，可得节点物理量的值，进而可表示出各单元内的近似解。

二、网格划分

计算区域：由于有环量的圆柱绕流问题左右对称（阻力为0）而上下不对称（升力不为0），因此计算圆柱左边的绕流区域即可。为了便于施加边界条件，体现环量的作用，将左上的1/4区域和左下的1/4区域分别划分网格计算（网格的生成直接利用对称性）。

本文编写了一份朴素的代码将待求解区域划分为三角形网格。总体来讲，首先分区并在每个子区域内均匀地取网格点，然后借助Header only constrained delaunay tessellator的C++代码中的三角剖分方法生成网格文件。示例网格如下图所示（分2层）

但由于在加大网格密度时计算效率不高，简便起见，利用Gmsh来生成误差分析所需的均匀三角网格。所有用到的网格已放在文件中。

三、有限元求解流程（总体与上一次相似）

1. 节点和单元的数据读取

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import math

如果是读取Gmsh生成的msh文件：

import meshio

# 读取 MSH 文件
mesh = meshio.read("D:/area_24.0_14.4_gird2.msh")

# 提取网格数据
points = mesh.points  # 点坐标
cells = mesh.cells    # 单元数据
# 还可以提取其他的网格属性，如单元类型、单元标签等

NP = points.shape[0]
NE = [cell_data for cell_data in cells if cell_data.type == 'triangle'][0].data.shape[0]

# 读取节点坐标X[0:NP,0]和X[0:NP,1]
X = np.zeros((NP, 2),dtype = float)
X = points[:,0:2]
X2 = np.zeros((NP, 2),dtype = float)
X2[:,0] = points[:,0]
X2[:,1] = - points[:,1]
# 读取单元节点对应关系数组NOD[0:NE,0:3]
NOD = np.zeros((NE,3),dtype = int)
NOD = [cell_data for cell_data in cells if cell_data.type == 'triangle'][0].data
#注意文件里的索引是从1开始的，而节点坐标数组X是从0开始的

如果是读取自己的网格程序生成的dat文件：

# 打开文件
try:
    with open('cylinder.dat', 'r') as f:
        # 读取节点数NP和单元数NE（自己生成的网格文件有些问题 实际的单元数比文件开头写的数量少）
        line = f.readline().strip()
        NP, NE_max = map(int, line.split())

        # 读取节点坐标X[0:NP,0]和X[0:NP,1]
        X = np.zeros((NP, 2),dtype = float)
        for i in range(NP):
            line = f.readline().strip()
            X[i] = np.array(list(map(float, line.split())))

        # 读取单元节点对应关系数组NOD[0:NE,0:3]
        NOD = np.zeros((NE_max,3),dtype = int)
        NE=0 #记录一下真实存在的单元数量
        for i in range(NE_max):
            line = f.readline().strip()
 
            if line:#读到文件末尾就结束，针对不知道单元确切数量的情况
                NOD[i] = np.array(list(map(int, line.split())))-1 
                NE+=1
            else:
                break
            #注意文件里的索引是从1开始的，而节点坐标数组X是从0开始的

except FileNotFoundError:
    print("文件不存在")
except Exception as e:
    print("文件读取失败：", e)

NOD = NOD[:NE, :]

2. 设置边界条件

#几何和流动参数
gamma = 5 #环量大小
r = 1
Rx= X[:,0].max()- X[:,0].min()
Ry = X[:,1].max()- X[:,1].min()

我们通过施加不同的边界条件来体现出有环量与无环量的不同。有环量的情况相当于绕圆柱额外施加一个环量为Gamma的平面点涡流动，易得其流函数为 $-\frac{\Gamma}{2\pi}ln(R)$ 。

根据圆柱绕流问题的定义，圆柱表面为流线，不妨设bc边界上 $\psi_{bc} = -\frac{\Gamma}{2\pi}ln(r)$ ；
ba边界上流函数不再是常数，设置ba上 $\psi_{ba} = -\frac{\Gamma}{2\pi}ln(R)$ ，R是到圆心的距离；
根据无穷远均匀来流（速度为1）的边界条件，ae边界与流线垂直， $\psi_{ae} = -\frac{\Gamma}{2\pi}ln(Rx) + y$ ；
de边界沿板仍为流线（外边界距离足够远时近似满足）， $\psi_{ed}= \psi_{e} = -\frac{\Gamma}{2\pi}ln(Rx) + Ry$ ；
增加的平面点涡流动仍然与cd边界垂直，无切向速度，仍然满足 $\frac{\partial \psi_{cd}}{\partial \mathbf{n}} =0$ 的自然边界条件。

#设置本质边界条件
Ψ = np.zeros(NP)
substantial_bound_index = []
unknown_index = []
for i in range(NP):
    if X[i,1] == 0 :
        Ψ[i] = - gamma*np.log(abs(X[i,0]))/(2*math.pi)
        substantial_bound_index.append(i)
    elif X[i,1] == Ry:
        Ψ[i] = Ry - gamma*np.log(abs(Rx))/(2*math.pi)
        substantial_bound_index.append(i)
    elif X[i,0] == -Rx:
        Ψ[i] = X[i,1] - gamma*np.log(Rx)/(2*math.pi)
        substantial_bound_index.append(i)
    elif abs(X[i,0]**2 + X[i,1]**2 - r*r)<= 1e-3:#如果网格尺度变化可能需要调整判断标准
        Ψ[i] = - gamma*np.log(r)/(2*math.pi)
        substantial_bound_index.append(i)
    else:
        unknown_index.append(i)

#验证本质边界条件的设置是否正确（主要是圆弧上的）
for i in substantial_bound_index:
    if(X[i,1]<=3 and X[i,0]>=-4):
        plt.scatter(X[i,0],X[i,1],alpha = 0.5,s=2)
plt.show()

3. 计算单元方程和整体方程

为了在网格加密时保持可接受的计算速度和存储效率，改用稀疏矩阵的存储方式。可处理的节点数量能达到数十万，解方程组的速度明显加快。

import scipy.sparse as sp
import scipy.sparse.linalg as splinalg

A_overall = sp.lil_matrix((NP,NP), dtype=float)
f_overall = np.zeros(NP) #整体方程的右端项，由于切向速度为0所以本来为0

for i in range(NE):#遍历所有单元，求单元方程的系数矩阵，并累加到整体方程的系数矩阵上
    X_i = np.zeros(3)
    Y_i = np.zeros(3)
    node_index = np.zeros(3)
    node_index = NOD[i,:] #是从0开始的
    X_i = X[node_index,0]
    Y_i = X[node_index,1]
    # print(X[2,1])
    A = 0.5*((X_i[1]-X_i[0])*(Y_i[2]-Y_i[0])-(Y_i[1]-Y_i[0])*(X_i[2]-X_i[0]))
    # print(i,A)
    #由于自己的网格文件有些问题，存在三点共线的情况，直接忽略掉
    （有限元最终的方程组是基于节点而非单元的，没有影响）
    if A==0:
        continue
    
    b1 = (Y_i[1]-Y_i[2])/(2*A)
    b2 = (Y_i[2]-Y_i[0])/(2*A)
    b3 = (Y_i[0]-Y_i[1])/(2*A)
    c1 = -(X_i[1]-X_i[2])/(2*A)
    c2 = -(X_i[2]-X_i[0])/(2*A)
    c3 = -(X_i[0]-X_i[1])/(2*A)
    A_overall[node_index[0],node_index[0]] += b1*b1 + c1*c1
    A_overall[node_index[1],node_index[1]] += b2*b2 + c2*c2
    A_overall[node_index[2],node_index[2]] += b3*b3 + c3*c3
    
    A_overall[node_index[0],node_index[1]] += b1*b2+c1*c2
    A_overall[node_index[1],node_index[0]] += b1*b2+c1*c2
    
    A_overall[node_index[0],node_index[2]] += b1*b3+c1*c3
    A_overall[node_index[2],node_index[0]] += b1*b3+c1*c3
    
    A_overall[node_index[1],node_index[2]] += b2*b3+c2*c3
    A_overall[node_index[2],node_index[1]] += b2*b3+c2*c3

#代入本质边界条件上的函数值，消元，只剩下待求节点的函数值
#计算消元后待求节点对应的右端项
for i in unknown_index:
    sum_f = 0
    for j in substantial_bound_index:
        sum_f += (-1)*A_overall[i,j]* Ψ[j]
    f_overall[i] = sum_f
#注：移项前的右端项为0，因为自然边界上切向速度为0

#首先得到待求解unknown_index节点变量所对应的A_tosolve系数矩阵（这里使用了一些稀疏矩阵的访问技巧）
import bisect
A_overall_coo = A_overall.tocoo()
A_tosolve = sp.lil_matrix((len(unknown_index), len(unknown_index)), dtype=float)

for i, j, val in zip(A_overall_coo.row, A_overall_coo.col, A_overall_coo.data): 
    #由于unknown_index是从小到大有序的，使用二分查找来加快速度
    idx_i = bisect.bisect_left(unknown_index, i)
    idx_j = bisect.bisect_left(unknown_index, j)

    if idx_i < len(unknown_index) and unknown_index[idx_i] == i and idx_j < len(unknown_index) and unknown_index[idx_j] == j:
        A_tosolve[idx_i, idx_j] = val


f_tosolve = f_overall[np.ix_(unknown_index)]
csc_A_tosolve = A_tosolve.tocsc()
# 在 CSC 矩阵上执行线性方程组求解，效率更高
sol = splinalg.spsolve(csc_A_tosolve, f_tosolve)

#得到完整的节点Ψ数组
pos = 0
for i in unknown_index:
    Ψ[i] = sol[pos]
    pos+=1

4. 计算单元和节点的流速和压强分布

首先利用前面计算出的节点流函数值，插值得到每个单元的流速；
然后，每个节点的流速则用相邻单元流速的加权平均（以单元面积为权重）得到；
最后，通过伯努利方程计算出节点的压强。

#计算单元的速度
vx = np.zeros(NE)
vy = np.zeros(NE)

#计算节点的速度——每个节点的速度采用相邻单元速度的面积加权平均
node_sum_area = np.zeros(NP) #每个节点相邻的累积面积
vx_node = np.zeros(NP)
vy_node = np.zeros(NP)

#遍历所有单元，顺便对相邻的节点更新其速度均值
for i in range(NE):
    X_i = np.zeros(3)
    Y_i = np.zeros(3)
    node_index = np.zeros(3)
    node_index = NOD[i,:] #是从0开始
    X_i = X[node_index,0]
    Y_i = X[node_index,1]
    
    A = 0.5*((X_i[1]-X_i[0])*(Y_i[2]-Y_i[0])-(Y_i[1]-Y_i[0])*(X_i[2]-X_i[0]))
    if A==0: #vx vy数组的中间会有一些单元是空的没赋值，但是没关系
        continue
    
    b1 = (Y_i[1]-Y_i[2])/(2*A)
    b2 = (Y_i[2]-Y_i[0])/(2*A)
    b3 = (Y_i[0]-Y_i[1])/(2*A)
    c1 = -(X_i[1]-X_i[2])/(2*A)
    c2 = -(X_i[2]-X_i[0])/(2*A)
    c3 = -(X_i[0]-X_i[1])/(2*A)
    
    vx[i] = c1*Ψ[NOD[i,0]]+c2*Ψ[NOD[i,1]]+c3*Ψ[NOD[i,2]]
    vy[i] = -b1*Ψ[NOD[i,0]]-b2*Ψ[NOD[i,1]]-b3*Ψ[NOD[i,2]]

    #更新节点的速度均值
    for j in range(3):
        s0 = node_sum_area[NOD[i,j]]
        vx0 = vx_node[NOD[i,j]]
        vx_node[NOD[i,j]] = (s0*vx0+A*vx[i])/(s0+A)
        vy0 = vy_node[NOD[i,j]]
        vy_node[NOD[i,j]] = (s0*vy0+A*vy[i])/(s0+A)
        node_sum_area[NOD[i,j]]+= A
        
#计算节点的压力
p_node = np.zeros(NP)
for i in range(NP):
    p_node[i] = 0.5*(1-vx_node[i]**2 - vy_node[i]**2)

5. 绘制流线图、流速和压强

先利用我们自己的数据来创建绘图网格（由于自己的网格有点问题，必须筛选出 valid_triangles）

from mpl_toolkits.mplot3d import Axes3D
from matplotlib.tri import Triangulation


def are_points_collinear(p1, p2, p3):
    """
    检查三个点是否共线
    """
    return abs(p1[0] * (p2[1] - p3[1]) + p2[0] * (p3[1] - p1[1]) + p3[0] * (p1[1] - p2[1])) <= 1e-16

# 用于存储有效的三角形索引
valid_triangles = []

# 检查三角形的拓扑关系数组 triangles
for triangle in NOD:
    p1, p2, p3 = X[triangle[0]], X[triangle[1]], X[triangle[2]]
    if not are_points_collinear(p1, p2, p3):
        # 顶点不共线，将三角形索引添加到有效的三角形数组中
        valid_triangles.append(triangle)


tri = Triangulation(X[:, 0], X[:, 1],triangles=valid_triangles)

#一、绘制数值解的流线图
z = Ψ
# 绘制等值线
levels = np.linspace(z.min(), z.max(), 80)
plt.tricontour(tri, z, levels=levels, colors='k')
plt.tricontourf(tri, z, levels=levels, cmap='viridis')
# 添加等值线标签
plt.colorbar()
plt.title('streamline _num')
plt.show()

#解析解的流线图
for i in range(NP):
    Ψ_true[i] = X[i, 1]*(1-1/(X[i,0]**2 + X[i,1]**2)) - gamma*np.log(X[i,0]**2 + X[i,1]**2)/(2*np.pi)
#其余都同上

四、实验结果与误差因素分析

1. 不同环量大小下流线图的变化

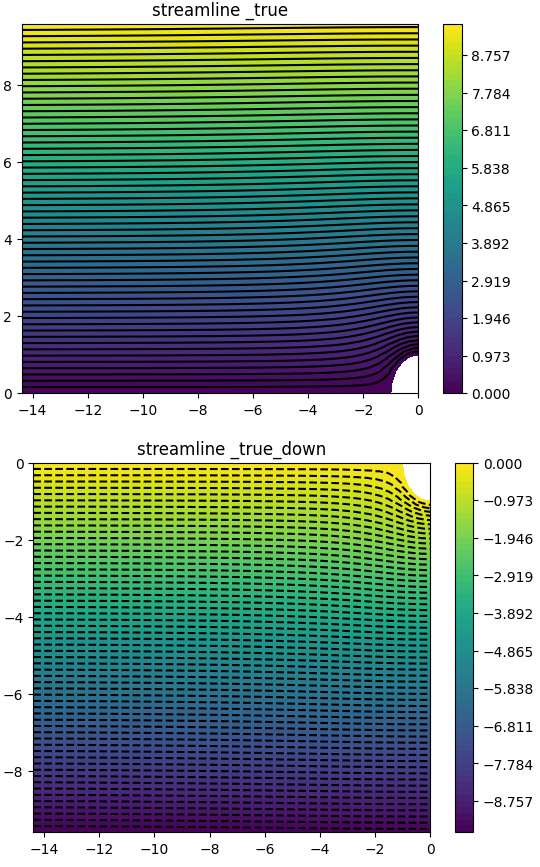
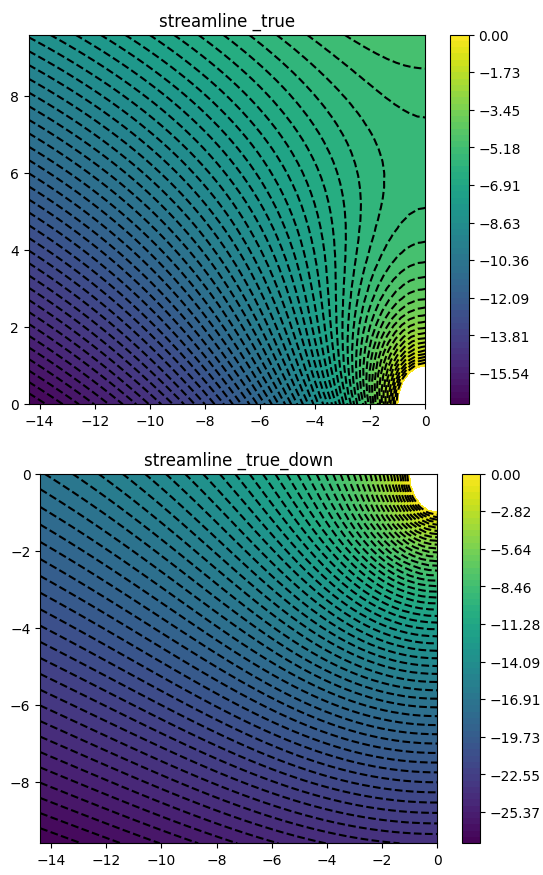
由于平面圆柱绕流是均匀来流、偶极子流和点涡流动的叠加，随着环量逐渐增大，围绕圆柱的点涡旋转流动逐渐超过了上下对称的绕开圆柱的流动，速度的驻点由圆的左端点沿柱面上移，最终离开柱面。

在没有环量时，有限元法的计算是相当精确的，如下图所示。环量增大会导致该模型的计算误差增大。下面的分析都选择环量为5（保证驻点在圆柱面上）的情况进行分析。

2. 分析外边界距离对误差的影响

2.1 前提：控制网格尺度几乎不变

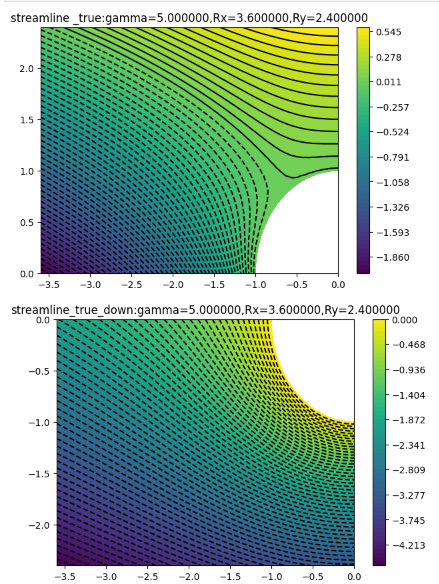
2.2 流线图比较

（3.6，2.4）

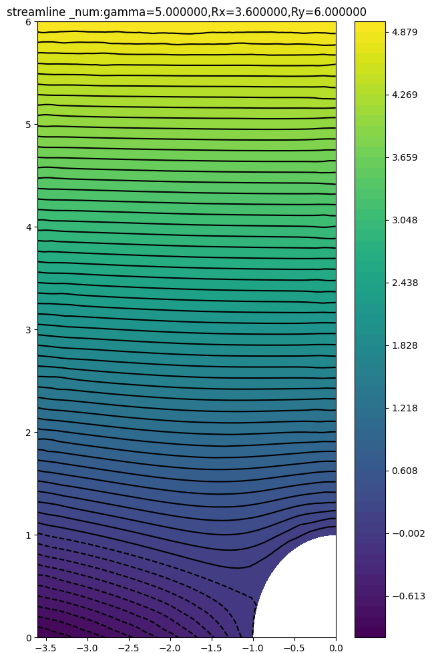
（3.6，6.0）

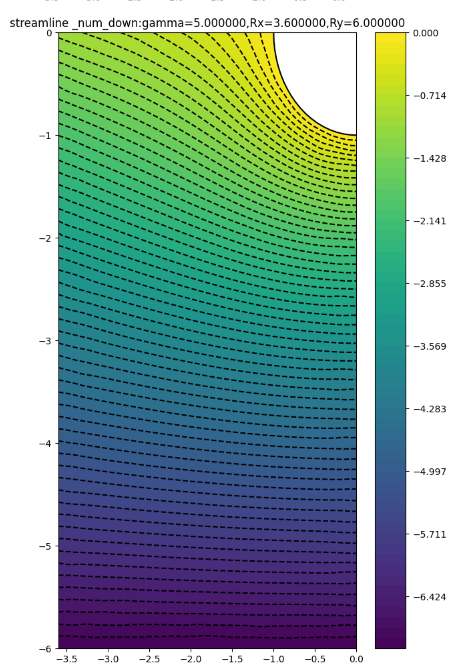
（3.6，9.6）

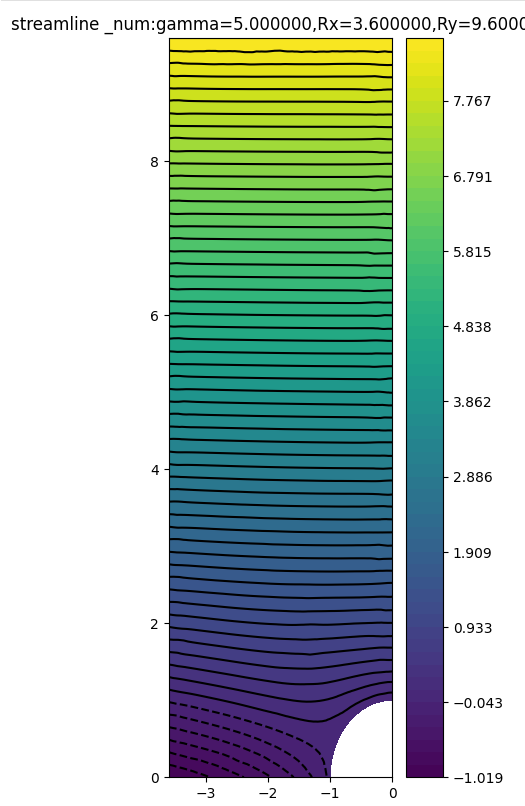
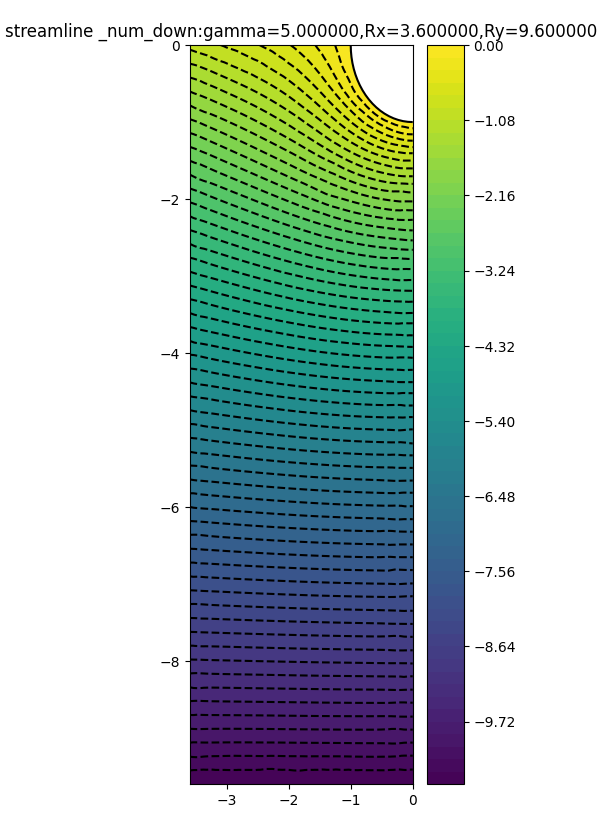
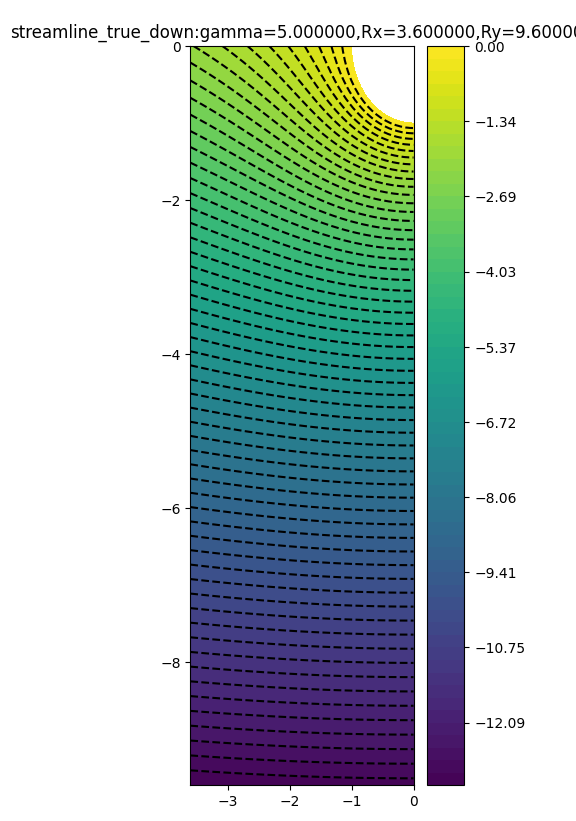
（14.4，6.0）

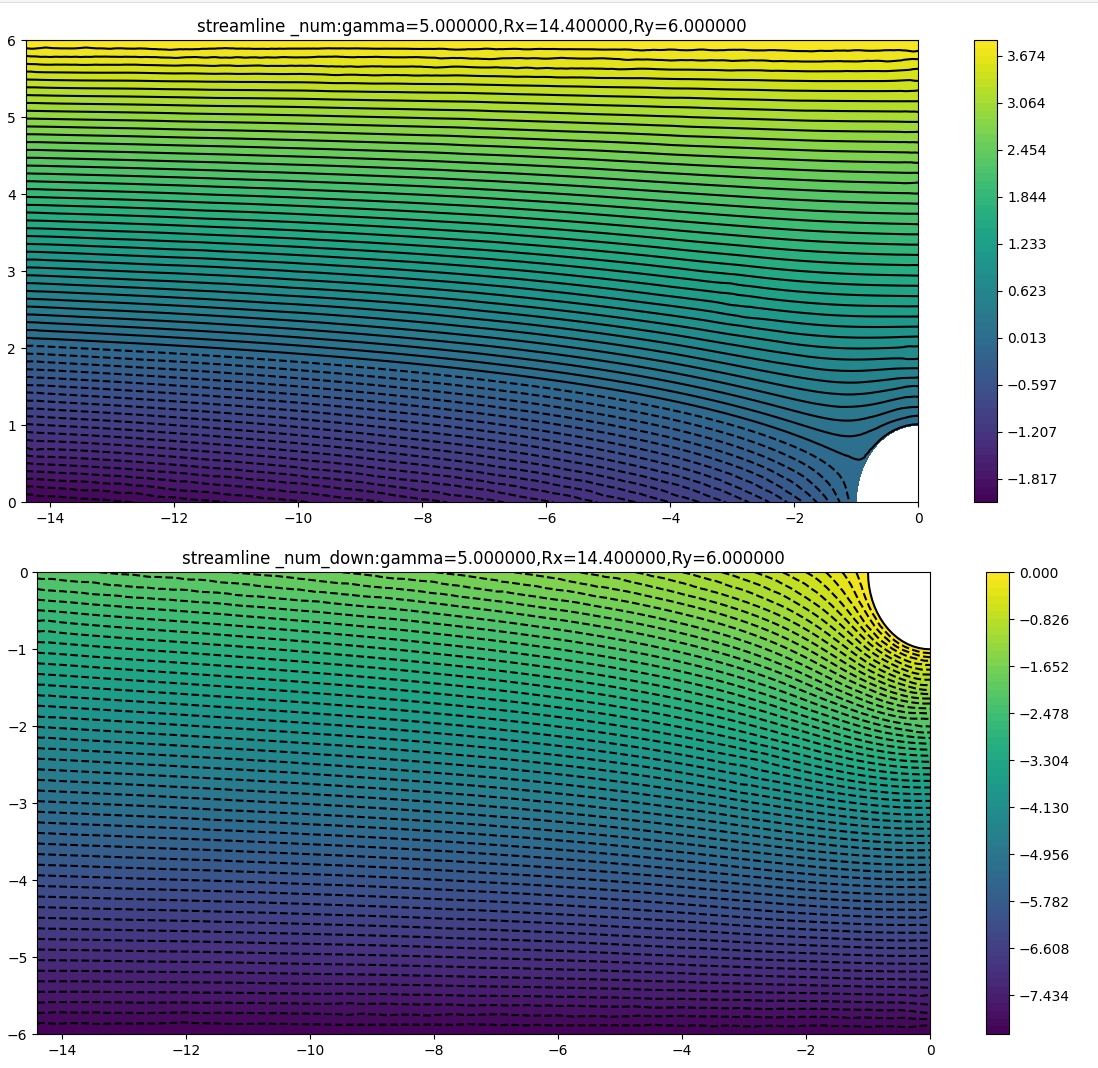
（10.8，9.6）

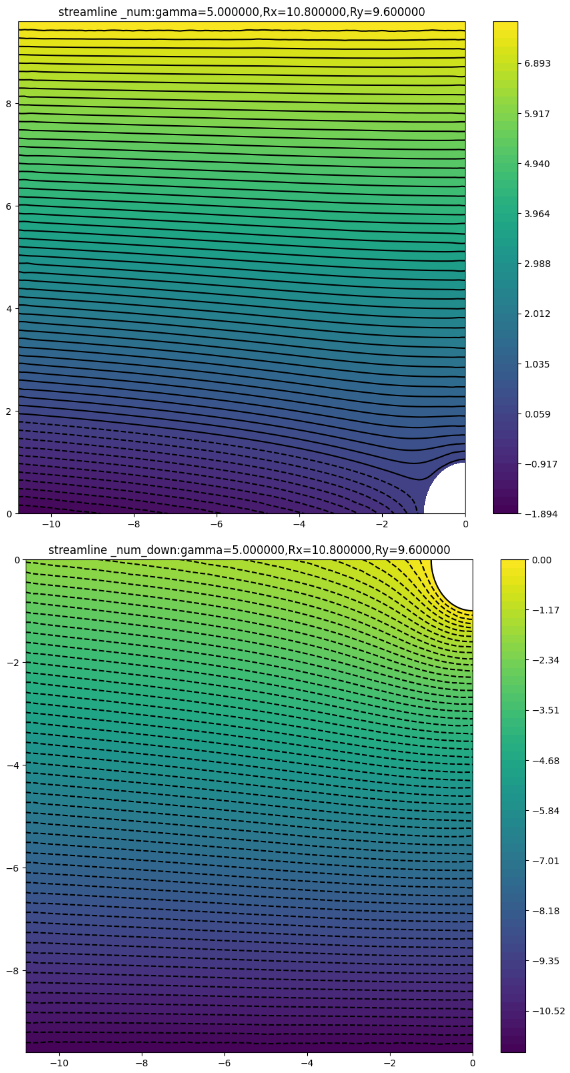
可以看到，对于有特定方向环量的圆柱绕流，上半区域存在驻点，数值解与解析解的流线差别较大，下半区域数值解与解析解的流线差别较小；随着外边界距离的扩大，外部区域受到点涡的影响减小，数值解与解析解变得更加接近，在左边界处和上边界处观察尤为明显。

2.3 右边界误差比较

注意：从下半部分图片的num_point 可以看到，右边界（y= -2.4 - 2.4范围内）网格点的数量都是相近的，排除了网格尺寸的影响。

Rx=3.6时，随着Ry增大，右边界上端点的误差由0.8逐渐减小到0.75左右，但变化不是特别明显；

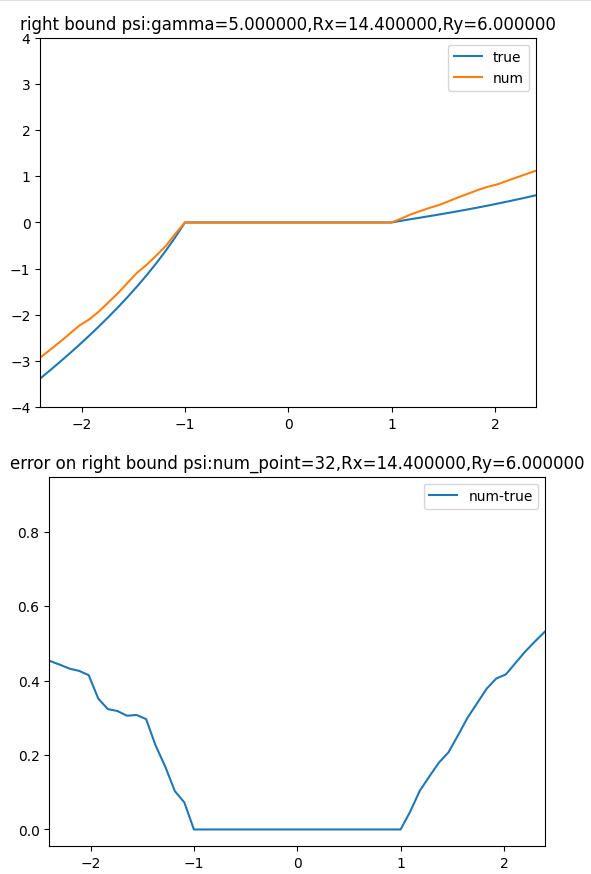
当Rx和Ry都取中等大小的值（10.8，9.6）时，误差降低到0.75以下，下降不是特别大；当Rx取到14.4和24时，误差下降到0.3-0.5之间（即便Ry=0.6），此时左边界是相对更加主要的影响因素。

2.4 左边界和上边界用解析解校准

如果将左边界和上边界的本质边界条件设置为解析解，观察到右边界上的误差明显减小、几乎消失，证明了方法的可靠性，同时说明误差的主要来源之一就是边界不满足无穷远条件。（图中负半轴的左半部分是未用解析解校准的部分，正半轴的右半部分是用解析解校准的部分，便于对比）

可以推断，当计算区域充分大时，可以计算出十分精确的结果。但受到计算速度的限制，这里就不再赘述了。

2.5 速度驻点位置比较

	（3.6，2.4）	（3.6，6.0）	（3.6，9.6）	（10.8，9.6）
计算驻点y	0.401695	0.401695	0.382683	0.422618
解析解驻点y	0.397887	0.397887	0.397887	0.397887
误差	0.003808	0.003808	-0.015204	0.024731

用速度最小值对应的节点来作为近似的速度驻点。可以看到，当网格尺寸不至于太大时，速度驻点的计算都是比较精确的，能比较好地反映出有环量的性质。

3. 分析网格尺度对误差的影响

3.1 流线图比较

在网格密度不至于太稀疏以至流线图不光滑时，流线图看起来都比较相近，因此不再详述。

3.2 右边界误差比较

在计算区域取得不太大时，误差随着网格尺寸的减小略有减小，不是特别明显；

在计算区域取得更大时，误差随着网格尺寸的减小（看图的下幅标题里num_points的变化）而减小更加迅速，此时网格尺寸对精度的影响更加明显；同时说明，足够大的外边界距离和不太稀疏的网格尺度缺一不可。

3.3 速度驻点位置比较

当网格尺寸变粗时，判断驻点时误差也相应地增大，很大原因是圆柱面上的节点数减少导致的。

综上所述，本文提出的有限元法计算二维无粘有环量圆柱绕流的数值结果可以与解析解较好吻合，误差随边界距离和网格尺度的变化符合物理和数学规律，是有效合理的。

百宝袋里是数学和代码

关注

1
点赞
踩
9

收藏

觉得还不错? 一键收藏
1
评论
有限元法计算二维圆柱绕流问题——无粘有环量的情况

写在前面该系列文章是笔者的学习记录，旨在通过分享促进交流加深理解，文中难免有许多纰漏与理解不当之处，若能批评指正必定感激不尽。侧重分享经典CFD方法的具体实现结果，详细的理论推导请参考教材。
复制链接

扫一扫