5-2-SVM

SVM

方向导数与梯度

1 方向导数

方向导数的本质是一个数值，简单来说其定义为：

		一个函数沿指定方向的变化率。

因此，构建方向导数需要有两个元素：
1.函数
2.指定方向
不一定是沿着坐标轴。

方向导数的数学表达式：

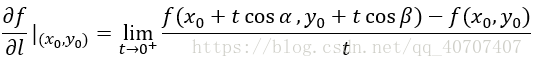
对于L 的单位向量是e=(cos α,cos β),而这正表示函数 f 沿着 L 方向的变化率。当我们让e=（1，0）时上述式子其实是 f 对于 x 的偏导数，即沿着 x 轴的变化率，而当让e=（0，1）时，上述式子便是 f 对于 y的偏导数，即沿着 y 轴的变化率。
对于二元函数，求方向导数的公式：

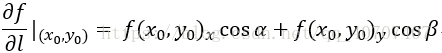
方向导数等于函数在 x 处的偏导数乘以单位向量的 x 部分加上在 y 处的偏导乘以单位向量的 y 部分，得到的值就是方向导数。从中也可以看出要求方向导数要先求它在 x 和 y 的偏导数，然后再求它方向的单位向量，最后做乘积加和得到结果。

与普通函数的导数类似，方向导数也不是百分之百存在的，需要函数满足在某点处可微，才能计算出该函数在该点的方向导数。
物理含义，采用最常用的下山图来表示

简单将上图看作是一座山的模型，我们处在山上的某一点处，需要走到山下。理论上来说，这座山的表面是可以通过一个函数的描述的（虽然想要找到这个函数可能很难），而这个函数可以在不同的方向上都确定出一个方向导数，这就好比于如果我们想下山，道路并不是唯一的，而是可以沿任何方向移动。区别在于有些方向可以让我们下山速度更快，有些方向让我们下山速度更慢，有些方向甚至引导我们往山顶走（也可以理解为下山速度时负的）。在这里，速度的值就是方向导数的直观理解。

2 梯度

梯度与方向导数是有本质区别的，梯度其实是一个向量，其定义为：
一个函数对于其自变量分别求偏导数，这些偏导数所组成的向量就是函数的梯度。
梯度定义方法：

公式中的i，j可分别表示为函数在x和y方向上的单位向量。

每个方向都是有方向导数的。
梯度：是一个矢量，其方向上的方向导数最大，其大小正好是此最大方向导数。

2.1 所有方向导数中有且仅有一个最大值

一个显而易见的物理现象：
光滑的、笔直的玻璃上的水滴，一定会沿着玻璃滑下来，（理想情况下）滑下来的方向就是玻璃最陡峭的地方。对于笔直的平面玻璃而言，这个滑下来的方向是只有一个。

梯度的数学定义：

具有一阶连续偏导数，意味着可微。可微意味着函数$f(x,y)$在各个方向的切线都在同一个平面上，也就是切平面。
所有的切线都在一个平面上，就好像刚才我说过的光滑的笔直玻璃上，某一点一定有且只有一个（梯度为0的情况除外，可以自己想想为什么？）最陡峭的地方（因为方向导数是切线的斜率，方向导数最大也就意味着最陡峭）。
这就解决了我对于“为什么所有方向导数中会存在并且只存在一个最大值”的疑问。
注意，因为这里举的例子是水滴往下滑，所以要说多说明一下，往下滑是梯度的反方向。因为梯度指的是增长最快的方向，而往下滑是减少最快的方向。

这个最大值的方向就是梯度方向。

3 方向导数与梯度的关系

函数在某点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。
证明：

当 $\theta =0$ 时，e 与梯度方向相同时，方向导数最大，函数增加最快
当 $\theta =\pi$ 时，e 与梯度方向相反时，方向导数最小，函数减少最快
当 $\theta =\pi /2$ 时，e 与梯度方向垂直时，方向导数为0， 函数变化率为零

方向导数是函数在各个方向的斜率，而梯度是斜率最大的那个方向，梯度的值是方向导数最大的值

采用下山的例子来解释。我们想要走到山下，道路有千万条，但总有一条可以让我们以最快的速度下山。当然，这里的最快速度仅仅作用在当前的位置点上，也就是说在当前位置A我们选择一个方向往山下走，走了一步之后到达了另外一个位置B，然后我们在B位置计算梯度方向，并沿该方向到达位置处c，重复这个过程一直到终点。但是，如果我们把走的每一步连接起来构成下山的完整路线，这条路线可能并不是下山的最快最优路线。

拉格朗日乘子法

1与原点的最短距离

方程为：
$$x^{2}y=3$$
求曲线上的点与原点的最短距离
图像：

解题思路：
与原点距离为a的点全部在半径为a的圆上，逐渐扩大圆的半径，第一次与x^2y=3相交的点就是距离原点最近的点。

此时，圆和曲线相切，也就是在该点切线相同：

2 等高线

可以看作函数的等高线：
$$f(x,y)=x^2+y^2$$

梯度向量：
$$\nabla f=\left(\begin{array}{c}\frac{\partial f}{\partial x}\\ \frac{\partial f}{\partial y}\end{array}\right)=\left(\begin{array}{c}2x\\ 2y\end{array}\right)$$
是等高线的法线：

另外一个函数$g(x,y)=x^{2}y$的等高线为：

因此，梯度向量：
$$\nabla g=\left(\begin{array}{c}\frac{\partial g}{\partial x}\\ \frac{\partial g}{\partial y}\end{array}\right)=\left(\begin{array}{c}2xy\\ x^2\end{array}\right)$$
也垂直于等高线$x^{2}y=3$：

梯度向量是等高线的法线，更准确地表述是：
梯度与等高线的切线垂直

拉格朗日乘数法

3.1 求解
$$\{\begin{array}{l}在极值点，圆与曲线相切\\ \\ 梯度与等高线的切线垂直\end{array}$$
在相切点，圆的梯度向量和曲线的梯度向量平行：

SVM（support vector machine）支持向量机：

支持向量机，因其英文名为support vector machine，故一般简称SVM，是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

线性分类器：

如果需要分类的数据都是线性可分的，那么只需要一根直线$f(x)=wx+b$就可以分开了，类似这样：

这种方法被称为：线性分类器，一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面（hyper plane）。也就是说，数据不总是二维的，比如，三维的超平面是面。但是有个问题：

上述两种超平面，都可以将数据进行分类，由此可推出，其实能有无数个超平面能将数据划分，但是哪条最优呢？

最大间隔分类器Maximum Margin Classifier：

对一个数据点进行分类，当超平面离数据点的“间隔”越大，分类的确信度（confidence）也越大。所以，为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。

用以生成支持向量的点，如上图XO，被称为支持向量点，因此SVM有一个优点，就是即使有大量的数据，但是支持向量点是固定的，因此即使再次训练大量数据，这个超平面也可能不会变化。
最大间隔分类器（maximum margin classifier）的目标函数可以定义为：

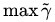
同时需满足一些条件，根据间隔的定义，有

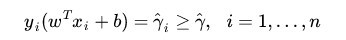
其中，s.t.，即subject to的意思，它导出的是约束条件。

非线性分类：

数据大多数情况都不可能是线性的，那如何分割非线性数据呢？


解决方法是将数据放到高维度上再进行分割，如下图：

当f(x)=x时，这组数据是个直线，如上半部分，但是当我把这组数据变为f(x)=x^2时，这组数据就变成了下半部分的样子，也就可以被红线所分割。

比如说，我这里有一组三维的数据X=（x1,x2,x3），线性不可分割，因此我需要将他转换到六维空间去。因此我们可以假设六个维度分别是：x1,x2,x3,x1^2,x1x2,x1x3，当然还能继续展开，但是六维的话这样就足够了。

新的决策超平面：d(Z)=WZ+b，解出W和b后带入方程，因此这组数据的超平面应该是：d(Z)=w1x1+w2x2+w3x3+w4*x1^2+w5x1x2+w6x1x3+b但是又有个新问题，转换高纬度一般是以内积（dot product）的方式进行的，但是内积的算法复杂度非常大。

从原始问题到对偶问题的求解

接着考虑之前得到的目标函数：


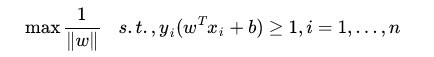
因为现在的目标函数是二次的，约束条件是线性的，所以它是一个凸二次规划问题。这个问题可以用现成的QP (Quadratic Programming) 优化包进行求解。一言以蔽之：在一定的约束条件下，目标最优，损失最小。

此外，由于这个问题的特殊结构，还可以通过拉格朗日对偶性（Lagrange Duality）变换到对偶变量 (dual variable) 的优化问题，即通过求解与原问题等价的对偶问题（dual problem）得到原始问题的最优解，这就是线性可分条件下支持向量机的对偶算法，这样做的优点在于：一者对偶问题往往更容易求解；二者可以自然的引入核函数，进而推广到非线性分类问题。

那什么是拉格朗日对偶性呢？简单来讲，通过给每一个约束条件加上一个拉格朗日乘子（Lagrange multiplier）$\alpha$，定义拉格朗日函数（通过拉格朗日函数将约束条件融合到目标函数里去，从而只用一个函数表达式便能清楚的表达出我们的问题）：

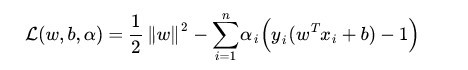
核函数Kernel：

我们会经常遇到线性不可分的样例，此时，我们的常用做法是把样例特征映射到高维空间中去。但进一步，如果凡是遇到线性不可分的样例，一律映射到高维空间，那么这个维度大小是会高到可怕的，而且内积方式复杂度太大。此时，核函数就隆重登场了，核函数的价值在于它虽然也是讲特征进行从低维到高维的转换，但核函数绝就绝在它事先在低维上进行计算，而将实质上的分类效果表现在了高维上，也就如上文所说的避免了直接在高维空间中的复杂计算。

几种常用核函数：

h度多项式核函数（Polynomial Kernel of Degree h）

高斯径向基和函数（Gaussian radial basis function Kernel）

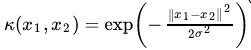
将原始空间映射为无穷维空间。如果$\sigma$选得很大的，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果$\sigma$选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。总的来说，通过调控参数$\sigma$，高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。下图所示的例子便是把低维线性不可分的数据通过高斯核函数映射到了高维空间：

S型核函数（Sigmoid function Kernel）

图像分类，通常使用高斯径向基和函数，因为分类较为平滑，文字不适用高斯径向基和函数。没有标准的答案，可以尝试各种核函数，根据精确度判定。

松弛变量：

数据本身可能有噪点，会使得原本线性可分的数据需要映射到高维度去。对于这种偏离正常位置很远的数据点，我们称之为 outlier ，在我们原来的 SVM 模型里，outlier 的存在有可能造成很大的影响，因为超平面本身就是只有少数几个 support vector 组成的，如果这些 support vector 里又存在 outlier 的话，其影响就很大了。

因此排除outlier点，可以相应的提高模型准确率和避免Overfitting的方式。

解决多分类问题：

经典的SVM只给出了二类分类的算法，现实中数据可能需要解决多类的分类问题。因此可以多次运行SVM，产生多个超平面，如需要分类1-10种产品，首先找到1和2-10的超平面，再寻找2和1,3-10的超平面，以此类推，最后需要测试数据时，按照相应的距离或者分布判定。

SVM与其他机器学习算法对比(图)：

代码

from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
x = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]  # 正态分布来产生数字,20行2列*2
y = [0] * 20 + [1] * 20  # 20个class0，20个class1

clf = svm.SVC(kernel='linear')
clf.fit(x, y)

w = clf.coef_[0]  # 获取w
a = -w[0] / w[1]  # 斜率
# 画图划线
xx = np.linspace(-5, 5)  # (-5,5)之间x的值
yy = a * xx - (clf.intercept_[0]) / w[1]  # xx带入y，截距

# 画出与点相切的线
b = clf.support_vectors_[0]
yy_down = a * xx + (b[1] - a * b[0])
b = clf.support_vectors_[-1]
yy_up = a * xx + (b[1] - a * b[0])

print("W:", w)
print("a:", a)

print("support_vectors_:", clf.support_vectors_)
print("clf.coef_:", clf.coef_)

plt.figure(figsize=(8, 4))
plt.plot(xx, yy)
plt.plot(xx, yy_down)
plt.plot(xx, yy_up)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80)
plt.scatter(x[:, 0], x[:, 1], c=y, cmap=plt.cm.Paired)  # [:，0]列切片，第0列

plt.axis('tight')

plt.show()

运行结果

参考：
支持向量机通俗导论（理解SVM的三层境界）

机器学习算法（一）SVM

SVM基本概念及Python实现代码

KKT条件