ADS仿真笔记(一) BJT直流仿真分析：模型参数、结果差异与厄尔利效应详解 ADS2020

​ 直流仿真是其他仿真的基础，只有在完成直流仿真、确定电路和系统直流工作点的情况下，才能进行其他仿真验证，可以说直流仿真是所有其它仿真的先决条件。

1. 基于模板的 BJT 直流仿真

ADS的直流仿真实验：

在仿真控制中可以由用户设置直流仿真时进行扫描方式（线性扫描、中心扫描、每频扫描等），通过BJT放大电路来解释基本操作和流程：在层次化中建设一个可以调用的放大器子电路，在仿真放大器中输出BJT器件的直流参数曲线，即BJT三极管的IC曲线对直流变量进行扫描，并打印输出数据。

1、设置工作空间

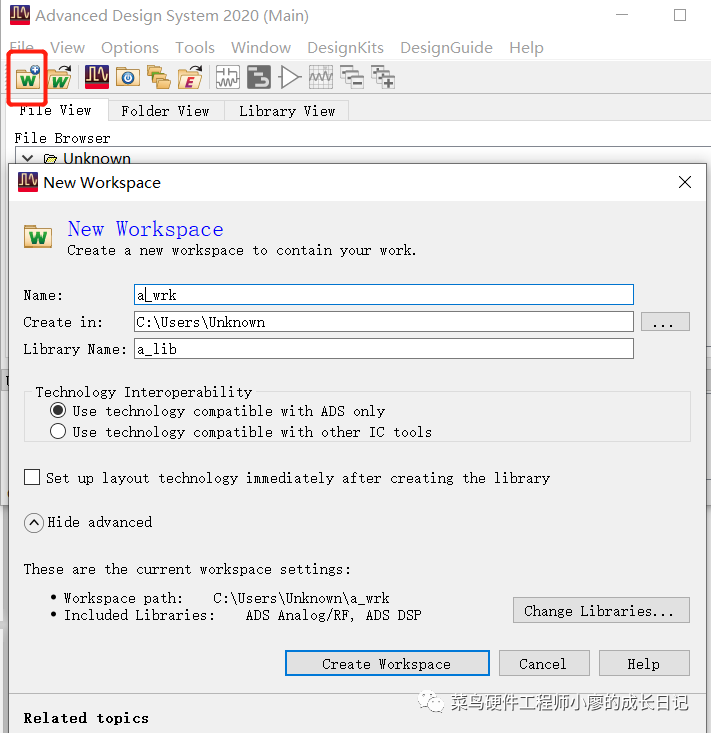
点击创建工作空间，Ads在2011以后都是工作空间取代了项目。

2、建立原理图

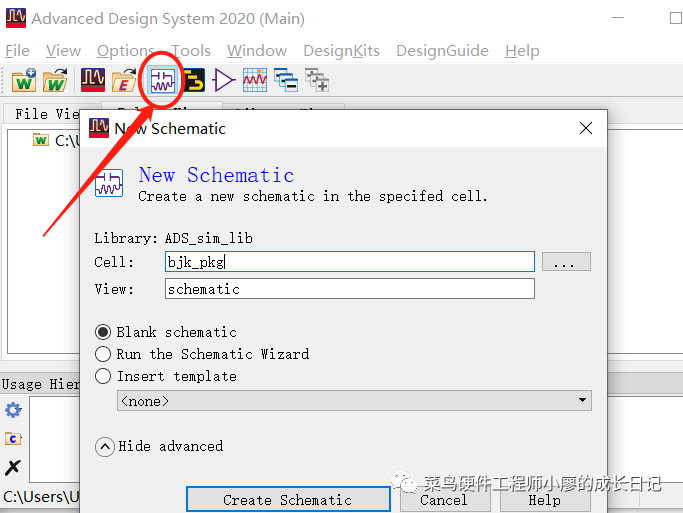
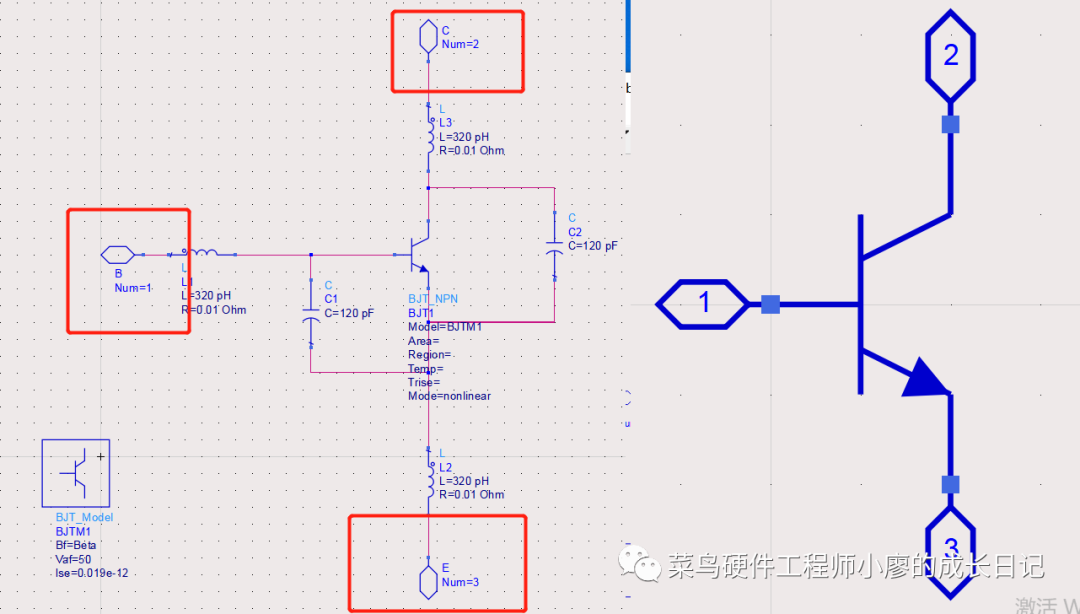
3、插入BJT组件和模型，在Device-BJT里面选出三极管和三极管模型

在Basic Componets中找到电容和电感。

4、连接好电路图

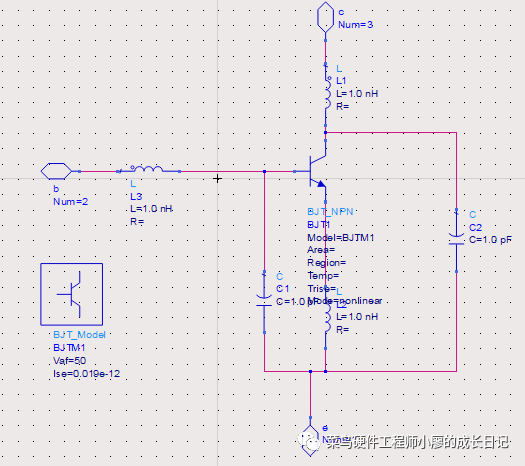
双击BJT_MODEL模型修改参数

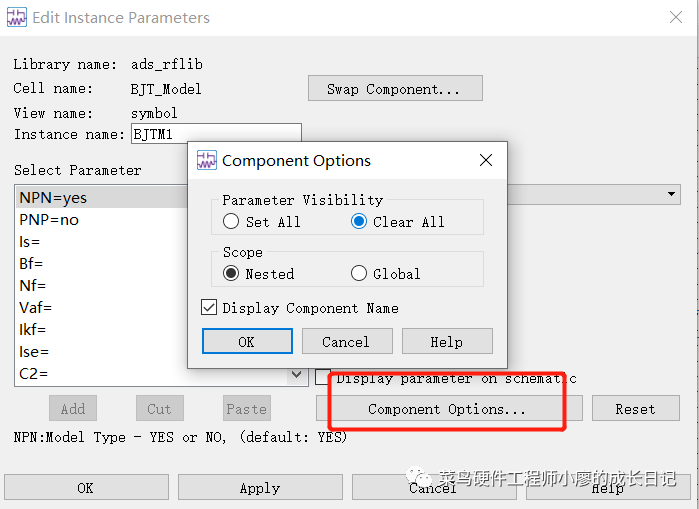
修改这些参数Bf=Beta，Ise=0.019e-2，Vaf=50，并且可见，display前面打勾。

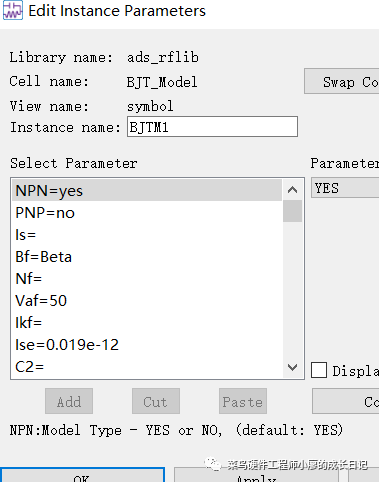
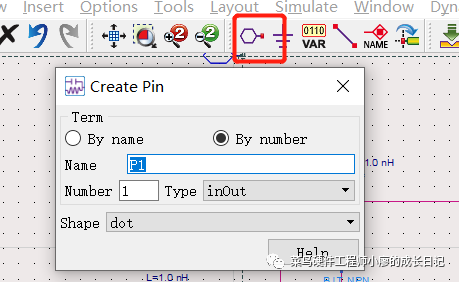
5、添加pin，在书上是的版本中为port，但是在2020版本中是pin，点击下面红色的，可以分别写为E、B、C

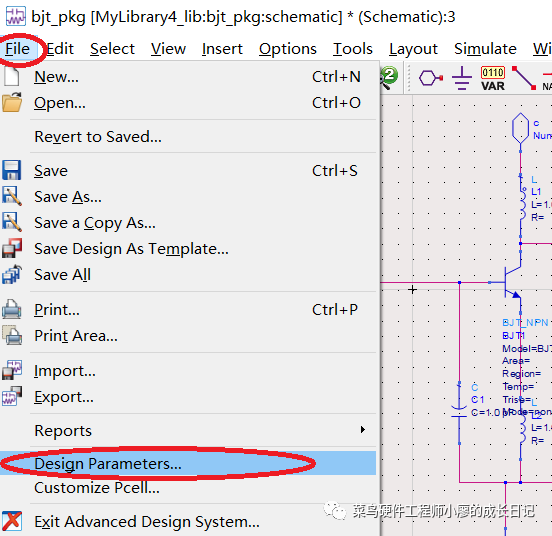
6、如果要修改symbol的名字，就是我们新建的这个元件的符号。File->Design Parameters

7、新建一个symbol，Window->Symbol

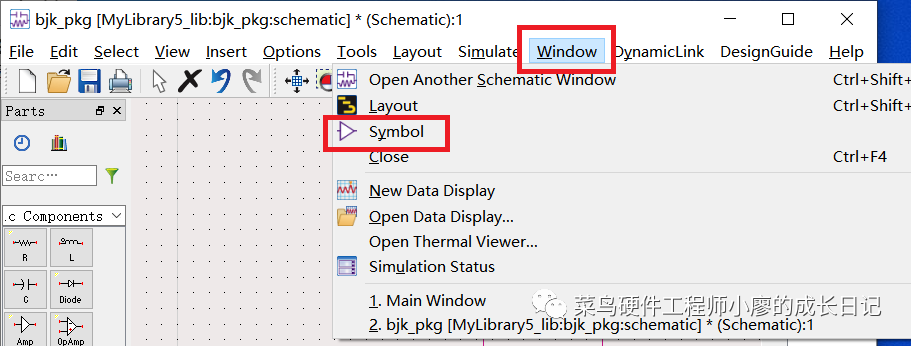
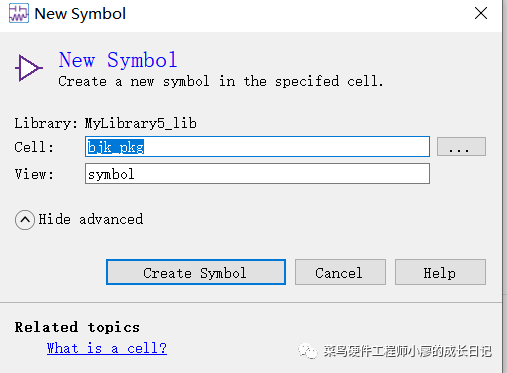
修改symbol的符号，即外观，按照下面的步骤来，并保存。

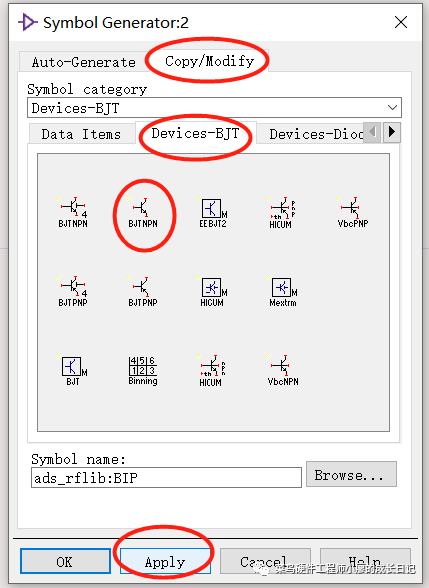
这里一定要注意pin的引脚顺序要和原理图中的一致，我当时没有一致检查了好久都没有仿真成功，当检查一致之后才成功了。生成的Symbol会自动有一个顺序，如果不一致删掉了之后用Insert->pin进行修改。

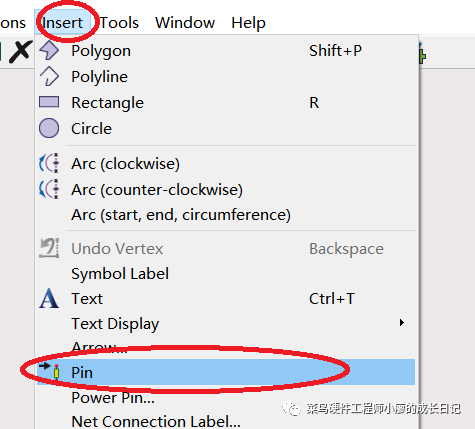
修改之后的顺序要对应上。

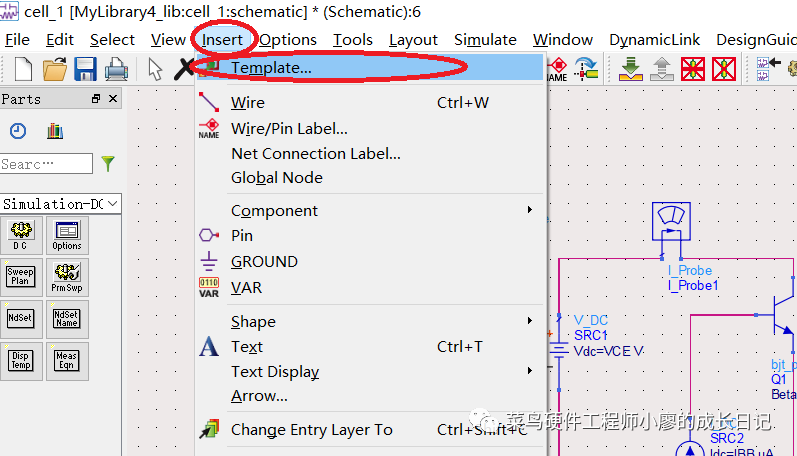
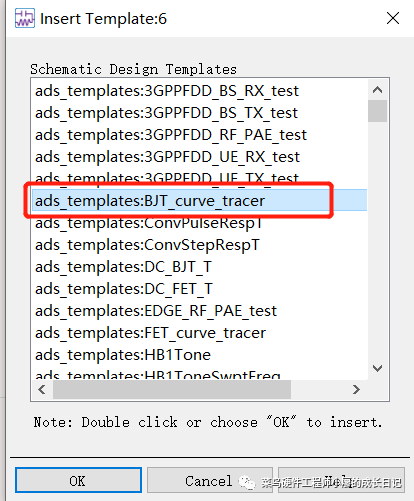
8、用新建的模型进行电路仿真，接下来新建一个原理图（前面已经说过了怎么新建），新建原理图之后，Insert->template->ads_templates:BJT_curve_tracer

添加模板

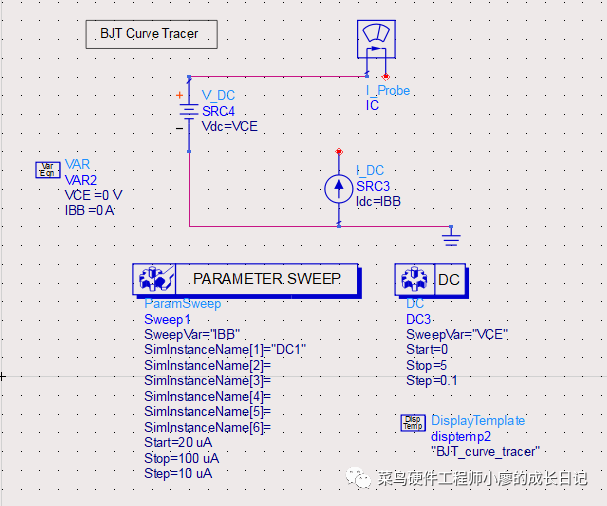
9、添加我们建好的三极管

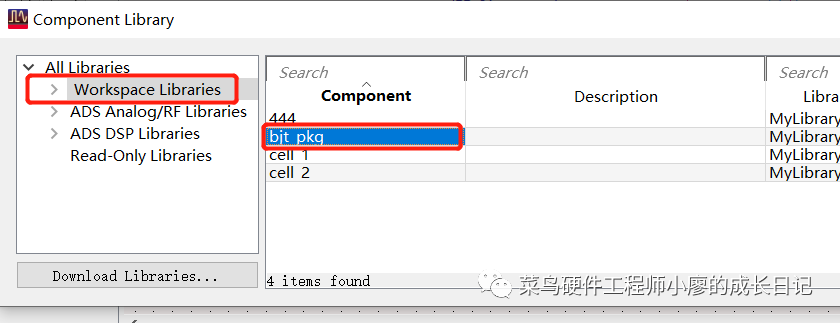
找到原来的工作空间，并将原来的模型导入

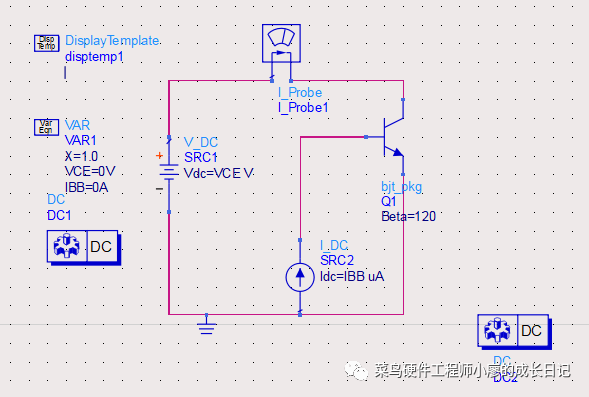
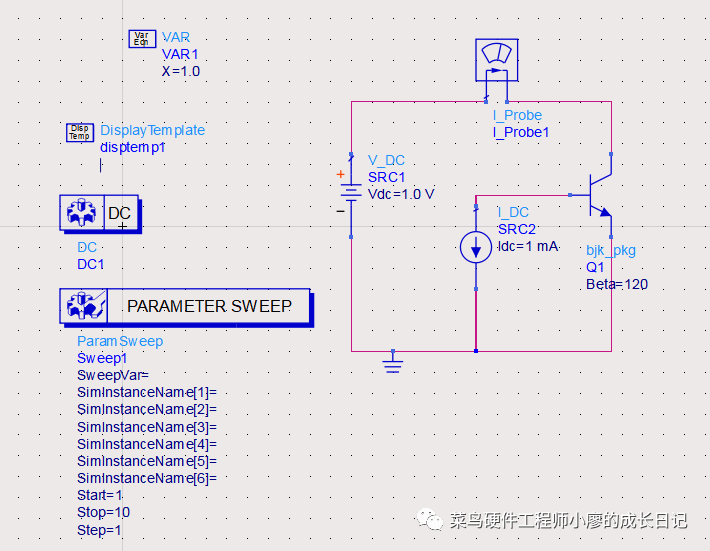
连线，并设置好IBB和VCE的参数，设置起始值和步进值，如下图：

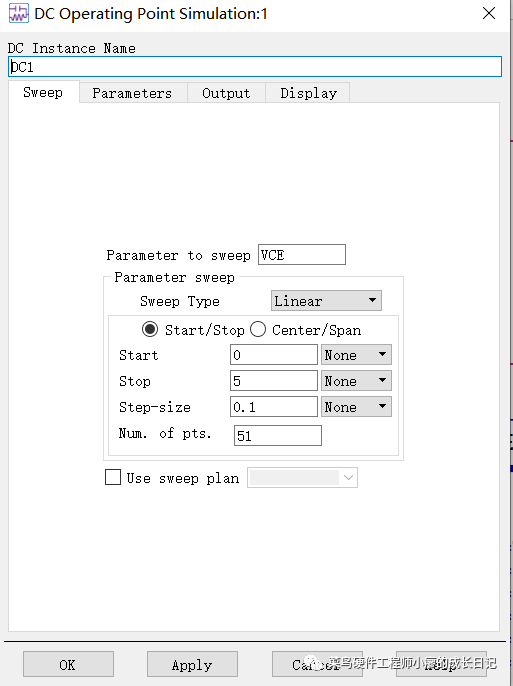
因为这个模板中很多设置已经设置好了，所以，直接运行仿真就可以看到效果。

10、开始仿真

也可以在菜单栏中选择Simulate->Simulate

同样也可以按F7进行开始仿真，仿真的结果如下。

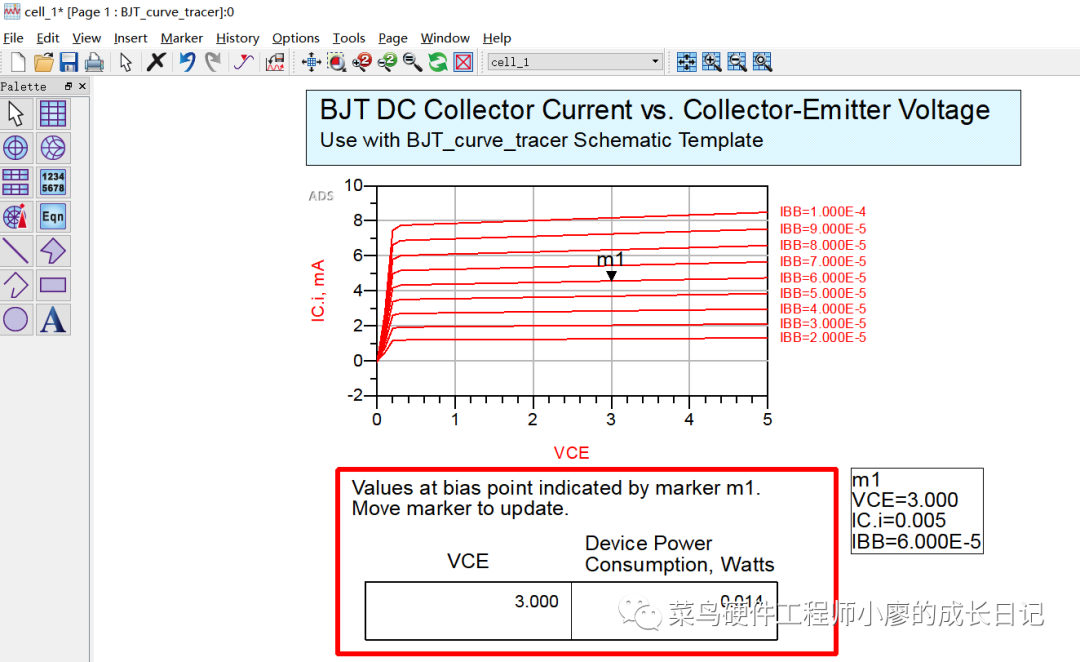
2. 非模板自定义控件仿真

建立仿真从第8步开始还可以，把这些控件单独拖出来，并单独设置进行下面的步骤。

1、新建原理图，在元件面板“Simulation-DC”中拖出“DC”、“PrmSwp”、“Dis Temp”，这里用来建立DC的仿真控件

2、三极管仿真，需要IBB和VCE，于是就在“Source-Freq Domin”中选择电源“V_DC”和“I_DC”

3、需要监测基极电流，这里要在“Probe Component”中选择一个电流探测器“I_Probe”

4、最重要的是从我们的建的模型中选择我们建的三极管

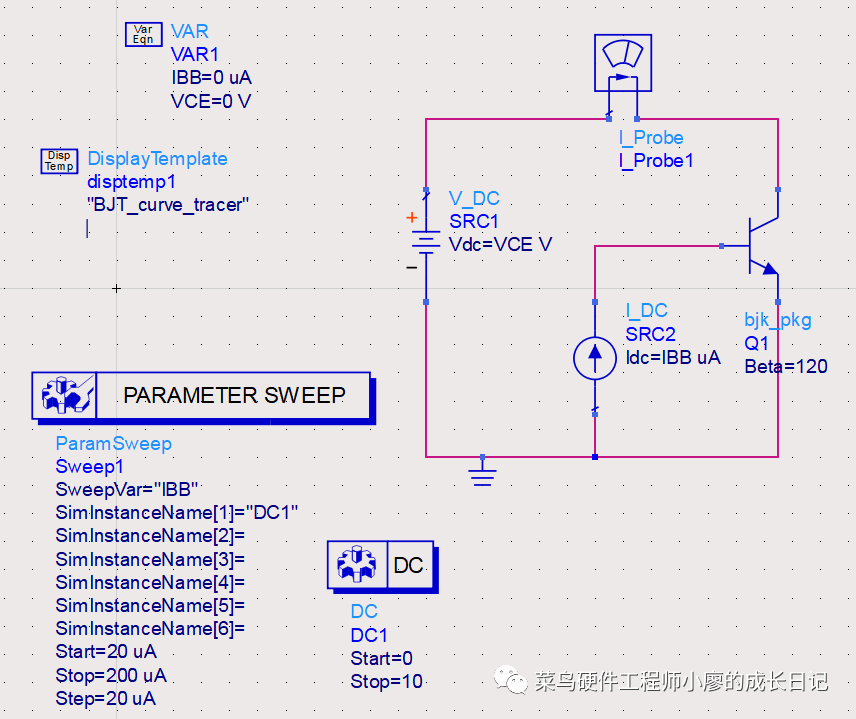
5、连线画图

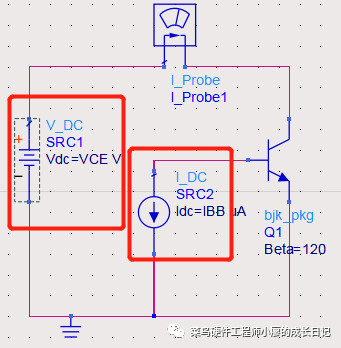
6、对电压源电流源进行设置，因为我需要将电压源电流源进行扫描，所以把Idc设置为IBB，Vdc设置为VCE，点击进去进行设置就行。

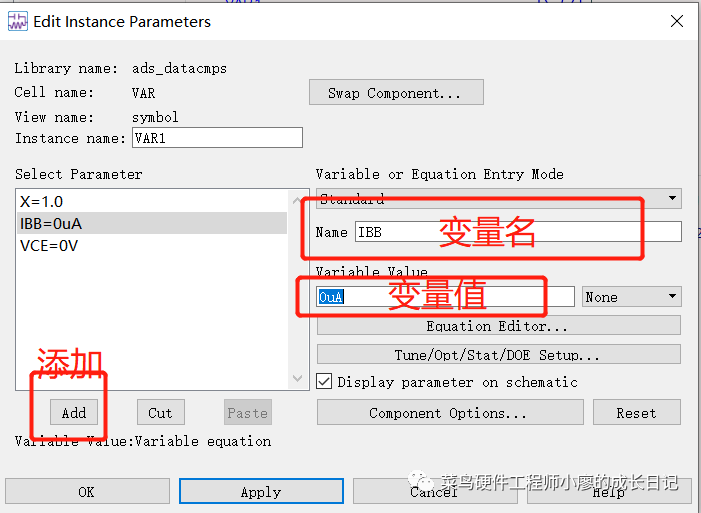
因为有了IBB和VCE这两个变量，所以就需要定义两个变量，点击，并对其进行赋值，添加之后点击Apply，OK。

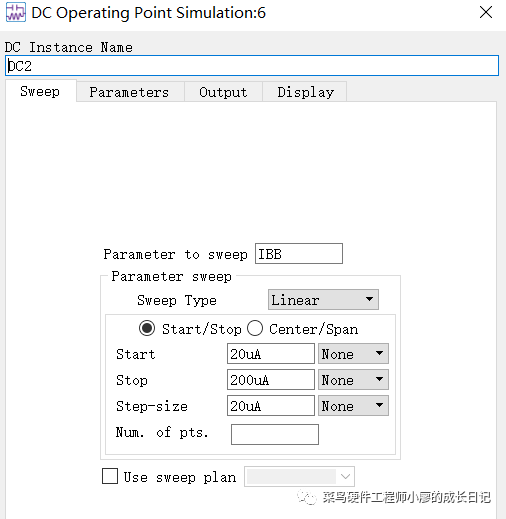
7、对直流控制器“Simulation-DC”进行设置电压的值，扫描的是VCE，方式是线性扫描，扫描的开始电压是0V，停止电压5V，步进是0.1V，点击OK

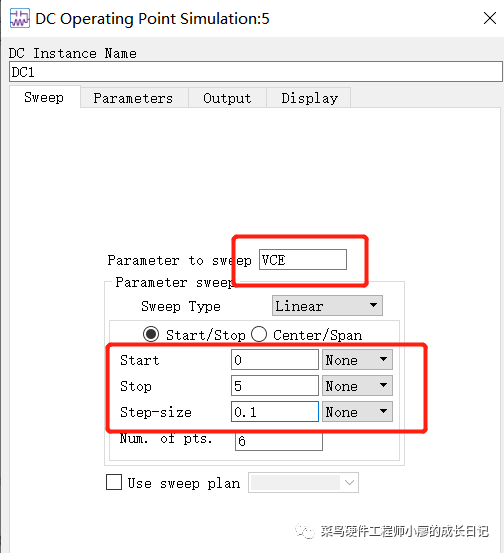
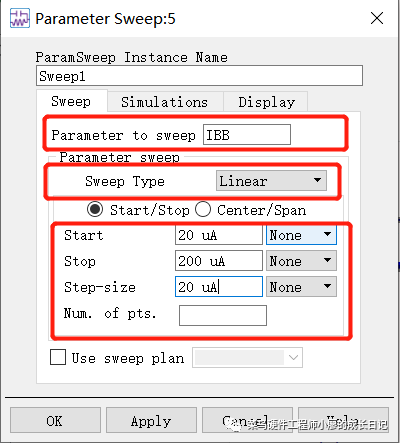
8、设置“Prm Swp”继续添加扫描的参数，设置扫描的参数是IBB，线性扫描，起始步进电流分别进行设置，如下。

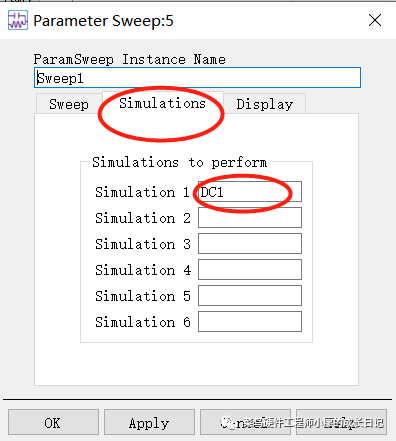
然后再选择”Simulation”，选择你是针对什么进行仿真，在第7步中的直流DC仿真控件的名字是”DC1”，所以要针对DC1直流仿真控制器进行参数扫描。最后点击”OK”

8、对显示控件进行设置，双击Disp Temp控件，在弹出的对话框中点击“Browse install templates”

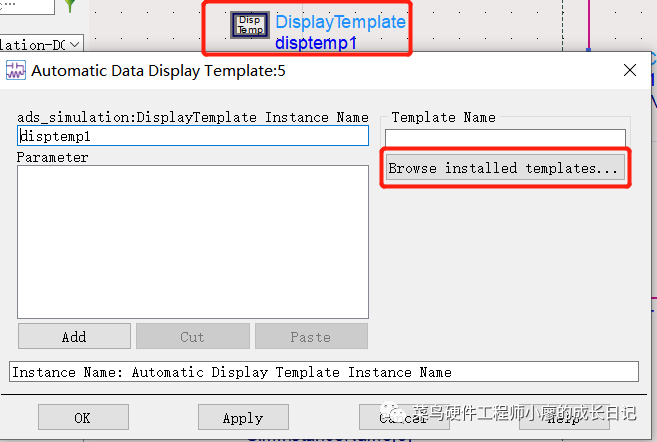
选择”BJT Curve trace”

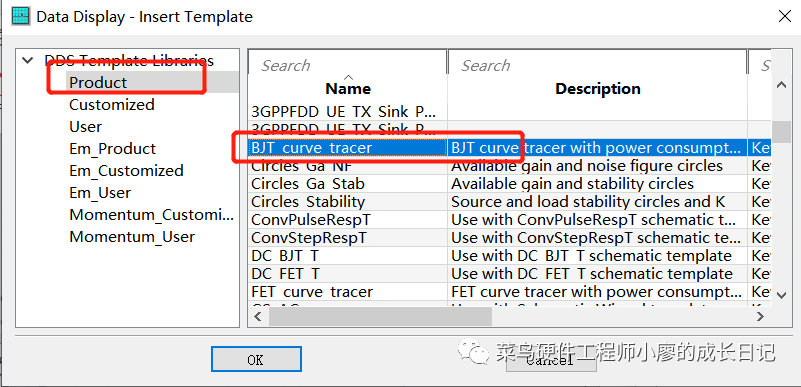
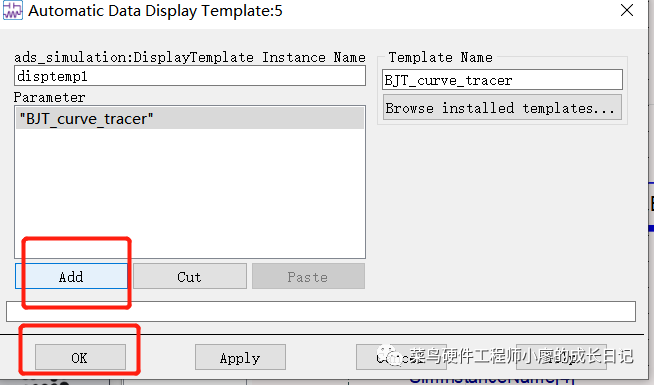
点击“ADD”->OK即可。

最后的原理图是这样的

点击仿真

发现什么都没有

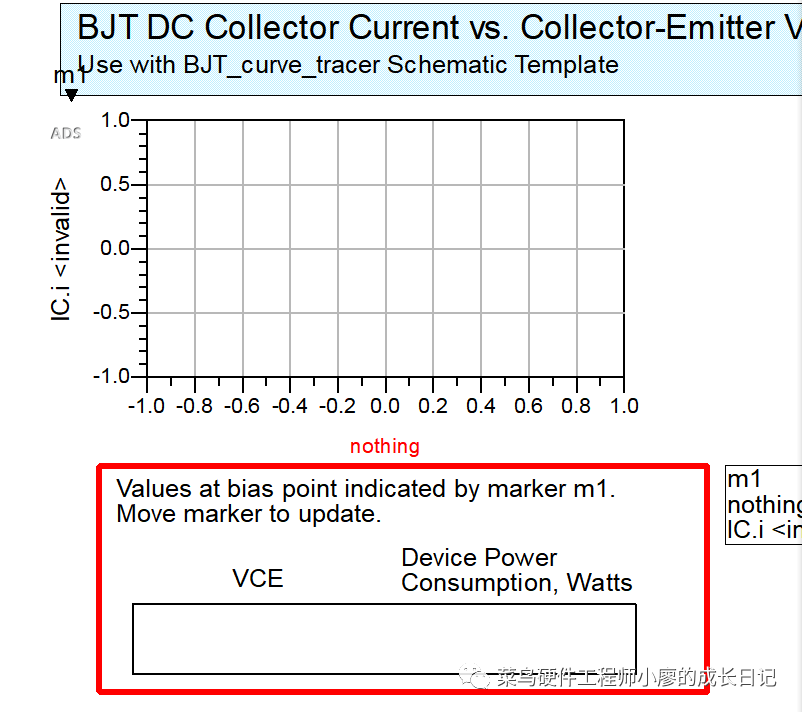
我观察纵坐标写的是IC.i，而在整个原理图中没有出现IC这个东西，所以我把它改为了“I_Probe1.i”

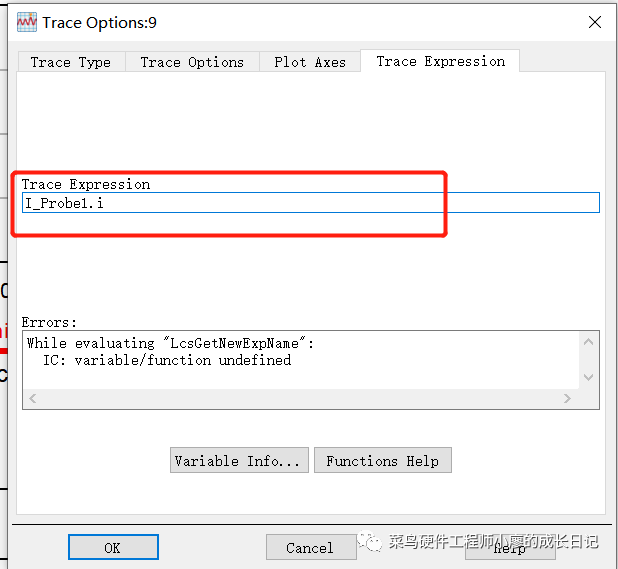
于是就出现了和上面的同样的效果

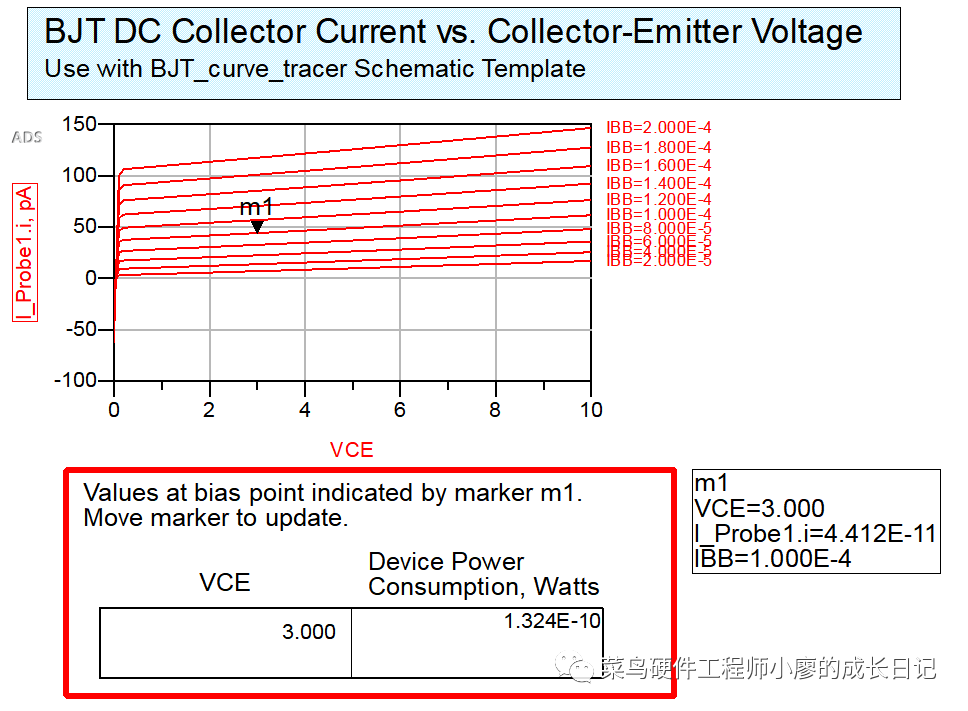
好了，今天的ADS的学习记录就到这里了，因为以前没有学过，而且参考书是针对2009的，而我用的是2020，照着书上来做不出来，有点慢，但是记录的都是我实践过的，希望对大家有帮助。

以上信息转载至微信公众号:菜鸟硬件工程师小摩的成长日记
https://mp.weixin.qq.com/s/iQ1aps5W5cMGTy7VoySXww

3. 实验结果分析

BJT参数中的Beta

​ 以上设定的 NPN 型 - BJT 管的增益 Beta (hFE) 定义为集电极电流 (Ic) 与基极电流 (Ib) 之比，在特定的集电极-发射极电压 (Vce) 和集电极电流 (Ic) 条件下：
$$\text{Beta (hFE)}=\frac{I_C}{I_B}$$
在这个仿真实验中，Beta=120意味着，在理想情况下，当BJT工作在放大区时，集电极电流将是基极电流的120倍。

仿真放大倍数与实际设置不符

1. 模型参数: Beta=120是BJT_test这个BJT模型的一个核心参数。ADS仿真器会使用这个值以及其他模型参数（如果定义了的话）来计算BJT在不同偏置条件下的行为。
2. 曲线追踪: 这个电路是一个BJT特性曲线追踪器。
   • I_DC (SRC2) 提供基极电流 IBB，这个电流值会通过ParamSweep进行扫描 (从20uA到200uA，步进20uA)。
   • V_DC (SRC1) 提供集电极-发射极电压 VCE，这个电压值会通过DC扫描控制器DC1进行扫描 (从0V到5V，步进0.1V)。
   • I_Probe (IC) 用来测量集电极电流 Ic。
3. 结果预期: 通过扫描不同的IBB和VCE，并测量对应的Ic，可以绘制出BJT的输出特性曲线（Ic vs Vce，以IBB为参数）。Beta=120这个参数将直接影响这些曲线的幅度和形状。例如，理想状态下对于给定的IBB，Ic的理论值大约是120 * IBB (在饱和区和击穿区之外)。
4. 实际结果:实际仿真得到的BJT直流电流放大倍数（Beta，即 Ic/Ib）在 90 - 100 倍，而不是之前简单模型中可能设置的更高值（例如120） ——其原因主要是因为晶体管在理想条件下的最大正向直流电流增益。然而，实际晶体管的电流增益 β (或 hFE) 并不是一个在所有工作条件下都保持恒定的值。它会受到晶体管实际工作点 (即具体的 IC 和 VCE 值) 以及温度等因素的显著影响。

• IC (集电极电流) 的影响：Beta通常在很小和很大的IC下都会下降。

• VCE (集电极-发射极电压) 的影响：厄尔利效应 (Early Effect)。由厄尔利电压 Vaf 描述，它使得 Ic 随 Vce 增加而增加，从而导致测量到的Beta随 Vce 增加而增加（在放大区）。

• 温度的影响：Beta通常随温度升高而增加

补充:厄尔利效应 (Early Effect)详解

厄尔利效应，又称基区宽度调制效应 (Base-Width Modulation)，是双极结型晶体管 (BJT) 中的一个重要物理现象，它描述了集电极-基极反向偏置电压 ($V_{CB}$)（或者近似地，集电极-发射极电压 ($V_{CE}$)）如何影响有效基区宽度，并进而影响晶体管的特性。该效应由詹姆斯·厄尔利 (James M. Early) 首次发现并阐释。

1. 物理机制

在 NPN 晶体管中，若发射结正偏、集电结反偏，则电子从发射极注入基区，穿越基区后被集电极吸收。

• 当集电极电压 $V_{CE}$ 增加时，集电结反偏程度加深 → 耗尽层向基区扩展 → 基区变窄（即有效基区厚度减小）。
• 基区变窄 → 载流子复合几率降低 → 发射极注入的电子更容易被集电极收集 → 电流 $I_C$增大。

这意味着：即使基极电压 VBEV 不变，增加 VCE 也会导致 IC 上升，打破理想三极管中 IC仅由 VBE 控制的假设。

2. 电特性表现

• 输出特性曲线的斜率：

厄尔利效应最直观的表现是在BJT的输出特性曲线（$I_C$ vs $V_{CE}$，以 $I_B$ 或 $V_{BE}$ 为参数）上。在理想情况下（无厄尔利效应），当BJT工作在正向放大区时，对于给定的基极电流 $I_B$，集电极电流 $I_C$ 应该不随 $V_{CE}$ 的变化而变化，即输出特性曲线应该是水平的。然而，由于厄尔利效应，当 $V_{CE}$ 增加时（近似于 $V_{CB}$ 增加），有效基区宽度减小，$I_C$ 随之增加。这使得输出特性曲线在放大区呈现出一定的正斜率。

• 厄尔利电压 ($V_{AF}$ 或 $V_A$)：

如果将输出特性曲线在放大区的部分反向延长，这些延长线大致会交于 $V_{CE}$ 轴的负半轴上的一点。这个电压的绝对值就被定义为厄尔利电压，用符号 $V_{AF}$ (正向工作模式下的厄尔利电压) 或简单记为 $V_A$ 表示。厄尔利电压是一个正值，典型值范围从几十伏特到几百伏特。$V_{AF}$ 越大，表明厄尔利效应越不显著，输出特性曲线越平坦，晶体管的输出电阻越高。反之，$V_{AF}$ 越小，厄尔利效应越显著，曲线斜率越大

3. 数学模型与影响

• 集电极电流的修正：考虑厄尔利效应后，集电极电流 (I_C) 的表达式通常被修正为：
  $$I_C\approx I_S\exp \left(\frac{V_{BE}}{V_T}\right)\left(1+\frac{V_{CE}}{V_{AF}}\right)$$
  其中：

  • $I_S$ 是反向饱和电流。

  • $V_{BE}$ 是基极-发射极电压。

  • $V_T$ 是热电压 ($kT/q$)。

  • $V_{CE}$ 是集电极-发射极电压。

  • $V_{AF}$ 是正向厄尔利电压。

• 对电流增益 (beta) 的影响：
  由于直流电流增益 $ \beta_{DC} = \frac{I_C}{I_B} $，并且 $I_C$ 现在包含了因子 $ \left(1 + \frac{V_{CE}}{V_{AF}}\right) $，这意味着即使理想的低 $V_{CE}$ 下的电流增益 Bf（即模型参数 Bf）是一个常数，实际测量到的 $ \beta_{DC} $ 也会随 $V_{CE}$ 的增加而增加：
  $$r_o={\frac{\partial V_{CE}}{\partial I_C}|}_{I_B=\text{const}}$$
  它使得 $I_C$ 随 $V_{CE}$ 增加而增加，从而导致测量到的Beta随 $V_{CE}$ 增加而增加（在放大区）

• 输出电阻 ($r_o$)：厄尔利效应直接决定了BJT的输出电阻 $r_o$。输出电阻定义为在基极电流 $I_B$ 恒定时，$V_{CE}$ 的变化与 $I_C$ 的变化之比的倒数：
  $$r_o=\frac{\partial V_{CE}}{\partial I_C}|\ast I_B=\text{const}$$
  可以近似地表示为：

$$r_o\approx \frac{V_{AF}+V_{CE}}{I_C}\approx \frac{V_{AF}}{I_{C,Q}}$$

其中 $I_{C,Q}$ 是静态工作点下的集电极电流。一个较大的 $V_{AF}$ 意味着较大的输出电阻，这在很多模拟电路设计中是期望的特性（例如，作为理想电流源的近似）。

4. 在电路设计中的意义

• 增益限制：在共射放大电路中，晶体管的输出电阻 $r_o$ 会与集电极负载电阻并联，从而限制了放大器的最大电压增益。

• 电流源性能：在设计电流镜或恒流源时，输出电阻 $r_o$ 是衡量电流源好坏的重要指标。厄尔利效应越弱（$V_{AF}$ 越大，$r_o$ 越大），电流源的性能越接近理想。

• 模型精度：在精确的电路仿真中，必须考虑厄尔利效应才能准确预测晶体管和电路的行为，尤其是在对输出阻抗、增益和频率响应有较高要求的模拟电路中。

多模拟电路设计中是期望的特性（例如，作为理想电流源的近似）。

4. 在电路设计中的意义

• 增益限制：在共射放大电路中，晶体管的输出电阻 $r_o$ 会与集电极负载电阻并联，从而限制了放大器的最大电压增益。

• 电流源性能：在设计电流镜或恒流源时，输出电阻 $r_o$ 是衡量电流源好坏的重要指标。厄尔利效应越弱（$V_{AF}$ 越大，$r_o$ 越大），电流源的性能越接近理想。

• 模型精度：在精确的电路仿真中，必须考虑厄尔利效应才能准确预测晶体管和电路的行为，尤其是在对输出阻抗、增益和频率响应有较高要求的模拟电路中。