信息论与编码2 期末复习-循环码

循环码

定义

设一个(n, k)线性分组码C，如果它的任一码字的每一次循环移位都还是C的一个码字，则称C是循环码。

例如：

特点

• 循环码是线性码
• 具有循环特性
  
  
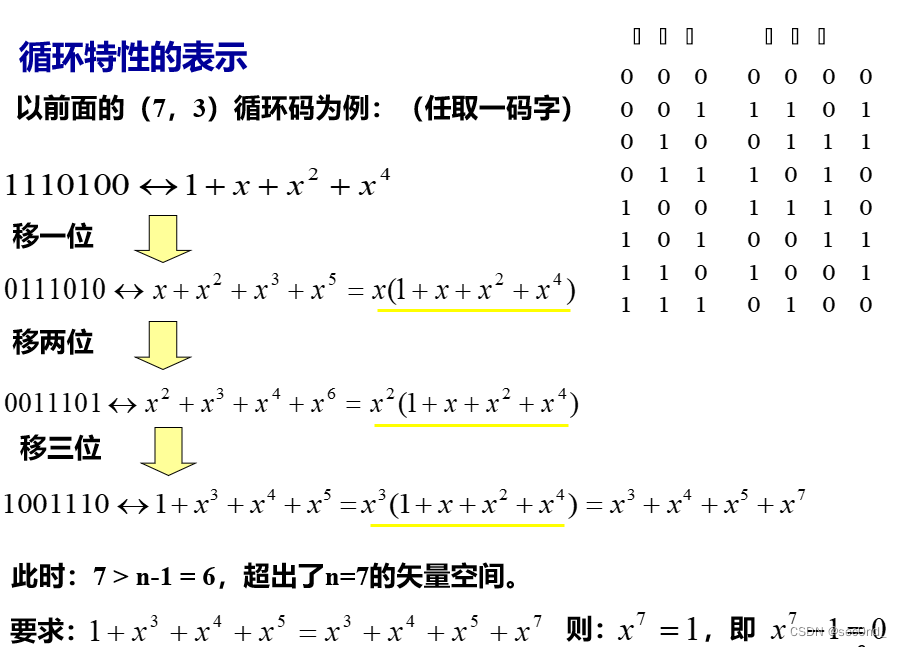
  总结：如果将一个循环码的某一非零码字用码多项式表示出来，那么其他的非零码字多项式就可以用这个码字多项式(或码字多项式的和)乘上x的一个幂，再求(xⁿ-1) 的余得到

编码

循环码的生成多项式

若g(x)是一个(n-k)次多项式，且是(xⁿ-1)的因式，则由g(x)可以生成一个（n，k）循环码，g(x)称为该循环码的生成多项式。

(n，k)循环码的构造

（1）对(x n - 1)做因式分解，找出(n – k)次因式；
（2）以该(n – k)次因式为生成多项式g(x)与不高于k – 1次信息多项式u(x)相乘，即得到对应消息序列的码多项式。

例：

生成矩阵

当循环码的生成多项式g（x）给定后，可以取g（x）本身加上移位k – 1次所得到的k – 1码字作为k个基底，即： g(x),xg(x),…,x^k1g(x)构成基底


例题：

校验矩阵

xⁿ-1 = g(x)·h(x)

由g (x)生成的码为C，在由h (x)生成的码就是C的对偶码C^⊥.

例题

构造

校验