基于XGBoost的中国GDP分析与预测（上）

从1950-2022年年度数据，导入包对数据进行分析处理，下载sklearn包，但是jupyter notebook显示numpy版本过高，输入代码pip install --upgrade numpy==1.14.5降低numpy版本兼容sklearn。直接pip下载xgboost包会失败，使用清华大学的pip镜像：pip install -i Simple Index xgboost即可下载成功。

2.1.2 数据指标含义

（1）国内生产总值：是一个国家所有常住单位在一定时期内生产活动的最终成果。GDP是国民经济核算的核心指标，也是衡量一个国家经济状况和发展水平的重要指标。

（2）国民总收入：原称国民生产总值，是指一个国家或地区所有常住单位在一定时期内所获得的初次分配收入总额。

（3）第一产业是指农、林、牧、渔业（不含农、林、牧、渔服务业）。

（4）第二产业是指采矿业（不含开采辅助活动），制造业（不含金属制品、机械和设备修理业），电力、热力、燃气及水生产和供应业，建筑业。

（5）第三产业即服务业，是指除第一产业、第二产业以外的其他行业。第三产业包括：批发和零售业，交通运输、仓储和邮政业，住宿和餐饮业，信息传输、软件和信息技术服务业等行业。

（6）人均国内生产总值(人均 GDP)顾名思义取决于两个因素:人口数和GDP。为人均GDP等于GDP总量除以年平均人口。

表2-1 指标单位及频次

指标名称	指标含义	单位	统计频次
x1	国内生产总值	亿元	年度
x2	国民总收入	亿元	年度
x3	第一产业增加值	亿元	年度
x4	第二产业增加值	亿元	年度
x5	第三产业增加值	亿元	年度
x6	人均国内生产总值	元	年度

2.2 数据清洗

2.2.1缺失数据处理

数据预处理质量决定了后续数据分析挖掘及建模工作的精度和泛化价值。在数据清洗过程中，主要处理的是缺失值、异常值和重复值。所谓清洗，是对数据集，进行丢弃、填充、替换、去重等操作，实现去除异常、纠正错误、补足缺失的目的。不同的数据存储和环境中对于缺失值的表示结果也不同，例如， Python返回对象是None,Pandas或Numpy中NaN空值。由于训练集属于官方数据，不用去除噪声数据。

调用data_train.info()判断存在空值的行与列，数据为73行6列，每列均存在缺失值，共71行不存在缺失值，显示结果如下

图2-1 检测缺失值

根据对数据的观察，在1950-1952年任何指标均为空值，所以填充方法不能使用均值填充，否则在1950年人均收入过万与实际情况不符合，选择前向填充，即用前一行的值填补空值。调用函数data_train.fillna(method='pad',axis=0)，参数axis是0，即使用前一行填充1950-1951年各项数据指标。

图2-2 充填缺失值

2.2.2清除冗余数据

根据国民总收入和人均国内生产总值的定义，人均国内生产总值等于国民总收入除以总人口，而且人均国内生产总值单位为元，不便于统计性描述等，故去除冗余数据人均国内生产总值，调用data_train.drop("人均国内生产总值(元)",axis=1)函数，指定参数axis为1就是删除列。

2.3 数据变换

2.3.1数据规范化处理

导入机器学习中的模块from sklearn import preprocessing，对数据经行标准化和归一化，选择数据为离散值且数据整体指数型递增，直接标准化会出现较多负值，GDP为负值容易参数经济落后的误解，使用标签编码对数据经行处理，其中LabelEncoder是用来对分类型特征值进行编码，即对不连续的数值或文本进行编码。其中包含以下主要方法：

（1）fit_transform(y)：相当于先进行fit再进行transform。

（2）inverse_transform(y)：根据索引值y获得原始数据，将数据反转换，当使用模型预测出来的数据，反转换为正常数据。

规范化后的数据和关键代码如下：

lbl = preprocessing.LabelEncoder()

y_train= lbl.fit_transform(y_train.astype(float))

y_test= lbl.fit_transform(y_test.astype(float))

图2-3 规范化后的数据

第3章国内生产总值年度数据分析

3.1 探索性数据分析

3.1.1数据描述性统计及可视化

通常我们拿到一份数据集，首先对获取的数据进行清洗，整理成本文所需要的新数据，然后再对新数据进行描述性统计分析，常用的是ptyhon中自带的描述性统计分析describe()函数。pandas有两个核心数据结构 Series和DataFrame，分别对应了一维的序列和二维的表结构。而describe()函数就是返回这两个核心数据结构的统计变量。其目的在于观察这一系列数据的范围、大小、波动趋势等等，为后面的模型选择打下基础。

描述性统计分析是用几个关键的数据指标来描述数据集的整体情况集中性和离散型。描述数据集常用4个指标：平均值、四分位数、标准差和标准分，利用这些指标可以进行数据的频数分析、数据的集中趋势分析、数据离散程度分析、数据的分布、以及一些基本的统计图形。本文选取全体指标和指标GDP（下文所有国内生产总值均用GDP表示）进行统计分析，调用函数data_train.describe()对全体指标进行分析，结果如下：

表3-1 各项指标统计分析

指标	样本数	平均值	最小值	最大值
国民总收入	73	175620.8	679.1	1197250.4
国内生产总值（GDP）	73	176525.3	679.1	1210207.2
第一产业增加值	73	16101.36	340.7	88345.1
第二产业增加值	73	73969.49	141.1	483164.5
第三产业增加值	73	86454.46	195.1	638697.6

Seaborn是一个用Python制作统计图形的库。它建立在matplotlib之上，并与pandas数据结构紧密集成。Seaborn可帮助探索和理解数据。它的绘图功能在包含整个数据集的数据框和数组上运行，并在内部执行必要的语义映射和统计汇总，以生成有用的图。seaborn.distplot单变量分布图，y轴表示密度，每个直方图的面积代表概率直方图（hist）+内核密度函数（kde），调用密度分布直方图，观察GDP数据的分布情况，在0区域分布多，可见我国从当年经济发展较落后到现在飞速增长的情况，但是从直方图分布并不能观察出数据分布特征。

关键代码：

data_train.describe()

sns.distplot(data_train['国内生产总值(亿元)'], color="r")

图3-1各项指标统计性描述

图3-2 指标GDP的直方图

3.1.2指标的相关性分析及可视化

随着大数据的蓬勃发展, 数据可视化技术也随之快速发展。由于大数据中捆绑着大量信息, 而热力图作为一种直观的可视化方法，具有综合展示数据地理空间特征和属性特征的良好特性, 可帮助各个领域的研究人员获取数据相关性知识[2]。

1）热力图原理

热力图体现了两个离散变量之间的组合关系。热力图也称之为交叉填充表，该图形最典型的用法就是实现列联表的可视化，即通过图形的方式展现两个离散变量之间的组合关系。热力图是一种通过对色块着色来显示数据的统计图表。绘图时，需指定颜色映射的规则。本题中较大的值由较鲜艳的颜色表示，较小的值由较深暗的颜色表示；较大的值由偏暖的颜色表示，较小的值由较冷的颜色表示。

图3-3 热力图颜色映射

2）相关系数热力图

热力图又名相关系数图。根据热力图中不同方块颜色对应的相关系数的大小，可以判断出变量之间相关性的大小。相关性最常用的是皮尔森相关系数，该系数是用来反映两个变量线性相关程度的统计量，使用公式：

ρ(X,Y)=Cov(X,Y)/(σXσY （3-1）

分母上的两个变量表示X和Y的标准差。皮尔森相关系数在[-1, 1]，越接近1或-1，表明正或反线性关系越强，为0则表示两个变量间没有线性关系。

3）指标间相关性分析

使用散点图描述GDP数据随着年度的分布情况，观察散点图发现GDP逐年飞速增加。加入影响因素进行预测时变量的选择是关键，将不同的影响因素引入模型进行预测可能会导致不同的预测精度。为筛选出合适的影响变量，首先计算出各影响指标与人均GDP指标的Pearson相关系数，明确变量间的相关程度，绘制相关系数热力图，其中对角线数据表示自己与自己的相关关系为1，没有意义，横纵坐标表示该行与该列之间的相关系数，最深色0.95为相关系数最小颜色最深，由图数据可知各项指标之间呈强正相关，即均大于0.75，在国民经济核算指标中完全可以使用国民总收入，第一产业增加值，第二产业增加值，第三产业增加值和人均国内生产总值预测国内生产总值。

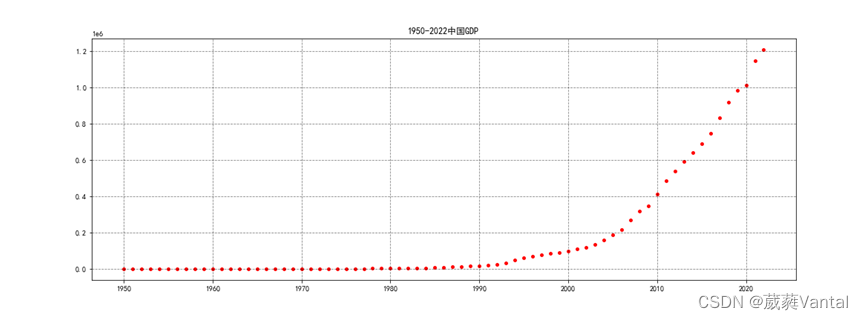
图3-4 年度GDP数据

图3-5 各项指标相关系数热力图

关键代码：ax =sns.heatmap(corr,annot=True,mask=mask，linewidth=0.5,

linewidths =.8, fmt='.2f', #只显示两位小数

annot_kws={"size":13}) ) # 设置每个单元格的距离

3.2数据集切分

3.2.1建立特征数据与标签数据

特征也可以称为属性，需要预测的结果称之为标签，本文选取国民总收入，第一产业增加值，第二产业增加值和第三产业增加值作为属性，预测标签国内生产总值。由于人均国内生产总值可以由国民生产总值推算出来，所有人均国内生产总值算是冗余数据，关键代码：

x=data_train.drop("国内生产总值(亿元)",axis=1)

x=data_train.drop("人均国内生产总值(元)",axis=1)

图3-6 属性与标签

3.2.2切分数据集

一组样本构成的集合称为数据集，一般将数据集分为两个部分，训练集和测试集。训练集中的样本是用来训练模型的，也叫训练样本，而测试集中的样本是用来训练模型好坏的，也叫测试样本。导入from sklearn.model_selection import train_test_split，调用train_test_split()函数，对数据集进行切分，X_train划分的训练集数据，X_test划分的测试集数据，y_train划分的训练集标签，y_test划分的测试集标签。其中参数test_size为0.2意思是样本数据分为训练集测试集之比8：2。由于GDP数据增长变化趋势有一定规律，为了防止模型过拟合，本文打乱数据集经行切分，设置参数shuffle=True，使得后续数据预测更加准确，其中核心代码：X_train,X_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=7)