线性代数及矩阵论（一）

线性代数原文 MIT 18.06 线性代数笔记
矩阵论笔记来自 工程矩阵理论
综合线性代数 机器学习的数学基础
配合视频 线性代数 工程矩阵理论

一、方程组的几何解释

我们从求解线性方程组来开始这门课，从一个普通的例子讲起：方程组有$2$个未知数，一共有$2$个方程，分别来看方程组的“行图像”和“列图像”。

有方程组$\{\begin{array}{llc}2x& -y& =0\\ -x& +2y& =3\end{array}$，写作矩阵形式有$\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$，通常我们把第一个矩阵称为系数矩阵$A$，将第二个矩阵称为向量$x$，将第三个矩阵称为向量$b$，于是线性方程组可以表示为$Ax=b$。

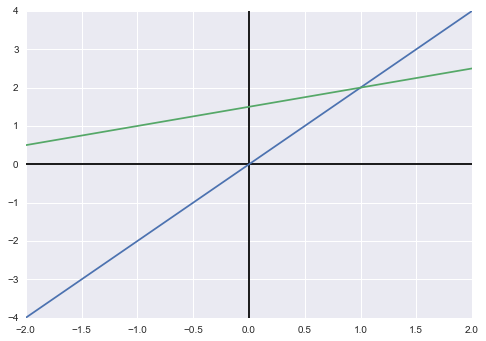
我们来看行图像，即直角坐标系中的图像：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

x = [-2, 2, -2, 2]
y = [-4, 4, 0.5, 2.5]

fig = plt.figure()
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')

plt.plot(x[:2], y[:2], x[2:], y[2:])

plt.draw()

plt.close(fig)

上图是我们都很熟悉的直角坐标系中两直线相交的情况，接下来我们按列观察方程组$x\left[\begin{array}{c}2\\ -1\end{array}\right]+y\left[\begin{array}{c}-1\\ 2\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$（我们把第一个向量称作$co{l}_1$，第二个向量称作$co{l}_2$，以表示第一列向量和第二列向量），要使得式子成立，需要第一个向量加上两倍的第二个向量，即$1\left[\begin{array}{c}2\\ -1\end{array}\right]+2\left[\begin{array}{c}-1\\ 2\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$。

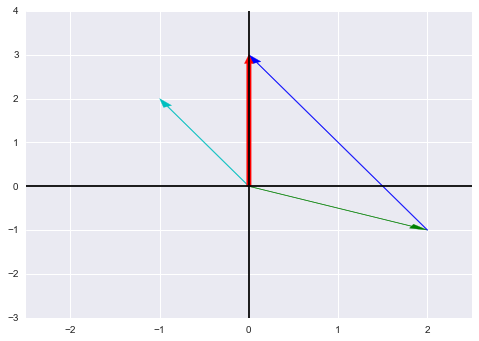
现在来看列图像，在二维平面上画出上面的列向量：

from functools import partial

fig = plt.figure()
plt.axhline(y=0, c='black')
plt.axvline(x=0, c='black')
ax = plt.gca()
ax.set_xlim(-2.5, 2.5)
ax.set_ylim(-3, 4)

arrow_vector = partial(plt.arrow, width=0.01, head_width=0.1, head_length=0.2, length_includes_head=True)

arrow_vector(0, 0, 2, -1, color='g')
arrow_vector(0, 0, -1, 2, color='c')
arrow_vector(2, -1, -2, 4, color='b')
arrow_vector(0, 0, 0, 3, width=0.05, color='r')

plt.draw()

plt.close(fig)

如图，绿向量$co{l}_1$与蓝向量（两倍的蓝绿向量$co{l}_2$）合成红向量$b$。

接着，我们继续观察$x\left[\begin{array}{c}2\\ -1\end{array}\right]+y\left[\begin{array}{c}-1\\ 2\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$，$co{l}_1,co{l}_2$的某种线性组合得到了向量$b$，那么$co{l}_1,co{l}_2$的所有线性组合能够得到什么结果？它们将铺满整个平面。

下面进入三个未知数的方程组：$\{\begin{array}{llcc}2x& -y& & =0\\ -x& +2y& -z& =-1\\ & -3y& +4z& =4\end{array}$，写作矩阵形式$A=\left[\begin{array}{ccc}2& -1& 0\\ -1& 2& -1\\ 0& -3& 4\end{array}\right],b=\left[\begin{array}{c}0\\ -1\\ 4\end{array}\right]$。

在三维直角坐标系中，每一个方程将确定一个平面，而例子中的三个平面会相交于一点，这个点就是方程组的解。

同样的，将方程组写成列向量的线性组合，观察列图像：$x\left[\begin{array}{c}2\\ -1\\ 0\end{array}\right]+y\left[\begin{array}{c}-1\\ 2\\ -3\end{array}\right]+z\left[\begin{array}{c}0\\ -1\\ 4\end{array}\right]=\left[\begin{array}{c}0\\ -1\\ 4\end{array}\right]$。易知教授特意安排的例子中最后一个列向量恰巧等于等式右边的$b$向量，所以我们需要的线性组合为$x=0,y=0,z=1$。假设我们令$b=\left[\begin{array}{c}1\\ 1\\ -3\end{array}\right]$，则需要的线性组合为$x=1,y=1,z=0x=1,y=1,z=0$。

我们并不能总是这么轻易的求出正确的线性组合，所以下一讲将介绍消元法——一种线性方程组的系统性解法。

现在，我们需要考虑，对于任意的$b$，是否都能求解$Ax=b$？用列向量线性组合的观点阐述就是，列向量的线性组合能否覆盖整个三维向量空间？对上面这个例子，答案是肯定的，这个例子中的$A$是我们喜欢的矩阵类型，但是对另一些矩阵，答案是否定的。那么在什么情况下，三个向量的线性组合得不到$b$？

——如果三个向量在同一个平面上，问题就出现了——那么他们的线性组合也一定都在这个平面上。举个例子，比如$co{l}_3=co{l}_1+co{l}_2$，那么不管怎么组合，这三个向量的结果都逃不出这个平面，因此当$b$在平面内，方程组有解，而当$b$不在平面内，这三个列向量就无法构造出$b$。在后面的课程中，我们会了解到这种情形称为奇异、矩阵不可逆、降秩矩阵。

下面我们推广到九维空间，每个方程有九个未知数，共九个方程，此时已经无法从坐标图像中描述问题了，但是我们依然可以从求九维列向量线性组合的角度解决问题，仍然是上面的问题，是否总能得到$b$？当然这仍取决于这九个向量，如果我们取一些并不相互独立的向量，则答案是否定的，比如取了九列但其实只相当于八列，有一列毫无贡献（这一列是前面列的某种线性组合），则会有一部分$b$无法求得。

接下来介绍方程的矩阵形式$Ax=b$，这是一种乘法运算，举个例子，取$A=\left[\begin{array}{cc}2& 5\\ 1& 3\end{array}\right],x=\left[\begin{array}{c}1\\ 2\end{array}\right]$，来看如何计算矩阵乘以向量：

• 我们依然使用列向量线性组合的方式，一次计算一列，$\left[\begin{array}{cc}2& 5\\ 1& 3\end{array}\right]\left[\begin{array}{c}1\\ 2\end{array}\right]=1\left[\begin{array}{c}2\\ 1\end{array}\right]+2\left[\begin{array}{c}5\\ 3\end{array}\right]=\left[\begin{array}{c}12\\ 7\end{array}\right]$
• 另一种方法，使用向量内积，矩阵第一行向量点乘$x$向量$\left[\begin{array}{cc}2& 5\end{array}\right]\cdot {\left[\begin{array}{cc}1& 2\end{array}\right]}^T=12,\left[\begin{array}{cc}1& 3\end{array}\right]\cdot {\left[\begin{array}{cc}1& 2\end{array}\right]}^T=7$。

教授建议使用第一种方法，将$Ax$看做$A$列向量的线性组合

• 关于矩阵的一些直观感受
• 矩阵乘法和矩阵的逆的意义

1.N矩阵

$N$矩阵为：$N_{n\times n}=\left[\begin{array}{cc}O& I_{n-1}\\ 0& O\end{array}\right]$，$N^k$就是把$1$斜向上推一次，$k\ge n时,N^k=0$。任意$Jordan$块都可以分解为$J_i={\lambda }_{i}E+N$

2.单位矩阵

文章中提到单位矩阵，大部分用$E$表示，某些用$I$表示，相关解释

二、矩阵消元

这个方法最早由高斯提出，我们以前解方程组的时候都会使用，现在来看如何使用矩阵实现消元法。

1.消元法

有三元方程组$\{\begin{array}{llcc}x& +2y& +z& =2\\ 3x& +8y& +z& =12\\ & 4y& +z& =2\end{array}$，对应的矩阵形式$Ax=b$为$\left[\begin{array}{ccc}1& 2& 1\\ 3& 8& 1\\ 0& 4& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}2\\ 12\\ 2\end{array}\right]$。

按照我们以前做消元法的思路：

• 第一步，我们希望在第二个方程中消去$x$项，来操作系数矩阵$A=\left[\begin{array}{ccc}\underline{1}& 2& 1\\ 3& 8& 1\\ 0& 4& 1\end{array}\right]$，下划线的元素为第一步的主元（pivot）：$\left[\begin{array}{ccc}\underline{1}& 2& 1\\ 3& 8& 1\\ 0& 4& 1\end{array}\right]\stackrel{ro{w}_2-3ro{w}_1}{\to }\left[\begin{array}{ccc}\underline{1}& 2& 1\\ 0& 2& -2\\ 0& 4& 1\end{array}\right]$

  这里我们先不管$b$向量，等做完$A$的消元可以再做$b$的消元。（这是MATLAB等工具经常使用的算法。）

• 第二步，我们希望在第三个方程中消去$y$项，现在第二行第一个非零元素成为了第二个主元：$\left[\begin{array}{ccc}\underline{1}& 2& 1\\ 0& \underline{2}& -2\\ 0& 4& 1\end{array}\right]\stackrel{ro{w}_3-2ro{w}_2}{\to }\left[\begin{array}{ccc}\underline{1}& 2& 1\\ 0& \underline{2}& -2\\ 0& 0& \underline{5}\end{array}\right]$

  注意到第三行消元过后仅剩一个非零元素，所以它就成为第三个主元。做到这里就算消元完成了。

再来讨论一下消元失效的情形：首先，主元不能为零；其次，如果在消元时遇到主元位置为零，则需要交换行，使主元不为零；最后提一下，如果我们把第三个方程$z$前的系数成$-4$，会导致第二步消元时最后一行全部为零，则第三个主元就不存在了，至此消元不能继续进行了，这就是下一讲中涉及的不可逆情况。

• 接下来就该回代（back substitution）了，这时我们在$A$矩阵后面加上$b$向量写成增广矩阵（augmented matrix）的形式：$\left[\begin{array}{cc}A& b\end{array}\right]=\left[\begin{array}{cccc}1& 2& 1& 2\\ 3& 8& 1& 12\\ 0& 4& 1& 2\end{array}\right]\to \left[\begin{array}{cccc}1& 2& 1& 2\\ 0& 2& -2& 6\\ 0& 4& 1& 2\end{array}\right]\to \left[\begin{array}{cccc}1& 2& 1& 2\\ 0& 2& -2& 6\\ 0& 0& 5& -10\end{array}\right]$

  不难看出，$z$的解已经出现了，此时方程组变为$\{\begin{array}{llcc}x& +2y& +z& =2\\ & 2y& -2z& =6\\ & & 5z& =-10\end{array}$，从第三个方程求出$z=-2$，代入第二个方程求出$y=1$，在代入第一个方程求出$x=2$。

2.消元矩阵

上一讲我们学习了矩阵乘以向量的方法，有三个列向量的矩阵乘以另一个向量，按列的线性组合可以写作$\left[v_1{v}_2{v}_3\right]\left[\begin{array}{c}3\\ 4\\ 5\end{array}\right]=3v_1+4v_2+5v_3$。

但现在我们希望用矩阵乘法表示行操作，则有$\left[\begin{array}{ccc}1& 2& 7\end{array}\right]\left[\begin{array}{ccc}& ro{w}_1& \\ & ro{w}_2& \\ & ro{w}_3& \end{array}\right]=1ro{w}_1+2ro{w}_2+7ro{w}_3$。易看出这里是一个行向量从左边乘以矩阵，这个行向量按行操作矩阵的行向量，并将其合成为一个矩阵行向量的线性组合。

介绍到这里，我们就可以将消元法所做的行操作写成向量乘以矩阵的形式了。

• 消元法第一步操作为将第二行改成$ro{w}_2-3ro{w}_1$，其余两行不变，则有$\left[\begin{array}{ccc}1& 0& 0\\ -3& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 2& 1\\ 3& 8& 1\\ 0& 4& 1\end{array}\right]=\left[\begin{array}{ccc}1& 2& 1\\ 0& 2& -2\\ 0& 4& 1\end{array}\right]$（左边矩阵的第$i$行可以计算得到结果矩阵的第$i$行，左边的矩阵按照行来读：结果矩阵的第一行是右边矩阵的（$1\times$第一行$+$$0\times$第二行$+$$0\times$第三行）这个结果；结果矩阵的第二行是右边矩阵的（$-3\times$第一行$+$$1\times$第二行$+$$0\times$第三行）这个结果；结果矩阵的第三行是右边矩阵的（$0\times$第一行$+$$0\times$第二行$+$$1\times$第三行）这个结果；，另外，如果三行都不变，消元矩阵就是单位矩阵$E=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$，$E$之于矩阵运算相当于$1$之于四则运算。）这个消元矩阵我们记作$E_{21}$，即将第二行第一个元素变为零。

• 接下来就是求$E_{32}$消元矩阵了，即将第三行第二个元素变为零，则$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& -2& 1\end{array}\right]\left[\begin{array}{ccc}1& 2& 1\\ 0& 2& -2\\ 0& 4& 1\end{array}\right]=\left[\begin{array}{ccc}1& 2& 1\\ 0& 2& -2\\ 0& 0& 5\end{array}\right]$。这就是消元所用的两个初等矩阵（elementary matrix）。

• 最后，我们将这两步综合起来，即$E_{32}(E_{12}A)=U$，也就是说如果我们想从$A$矩阵直接得到$U$矩阵的话，只需要$(E_{32}{E}_{21})A$即可。注意，矩阵乘法虽然不能随意变动相乘次序，但是可以变动括号位置，也就是满足结合律（associative law），而结合律在矩阵运算中非常重要，很多定理的证明都需要巧妙的使用结合律。

既然提到了消元用的初等矩阵，那我们再介绍一种用于置换两行的矩阵：置换矩阵（permutation matrix）：例如$\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]=\left[\begin{array}{cc}c& d\\ a& b\end{array}\right]$，置换矩阵将原矩阵的两行做了互换。顺便提一下，如果我们希望交换两列，则有$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}b& a\\ d& c\end{array}\right]$。

我们现在能够将$A$通过行变换写成$U$，那么如何从$U$再变回$A$，也就是求消元的逆运算。对某些“坏”矩阵，并没有逆，而本讲的例子都是“好”矩阵。

3.逆

现在，我们以$E_{21}$为例，$[?]\left[\begin{array}{ccc}1& 0& 0\\ -3& 1& 0\\ 0& 0& 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$，什么矩阵可以取消这次行变换？这次变换是从第二行中减去三倍的第一行，那么其逆变换就是给第二行加上三倍的第一行，所以逆矩阵就是$\left[\begin{array}{ccc}1& 0& 0\\ 3& 1& 0\\ 0& 0& 1\end{array}\right]$。

我们把矩阵$E_{ij}$的逆记作$E_{ij}^{-1}$，所以有$E_{ij}^{-1}{E}_{ij}=E$。

• 求解逆矩阵的常用三种方法

矩阵逆的性质有：

1. $(A^{-1}{)}^{-1}=A$
2. $(\lambda A{)}^{-1}=\frac{1}{\lambda }A$
3. $(AB{)}^{-1}=B^{-1}{A}^{-1}$
4. $(A^T{)}^{-1}=(A^{-1}{)}^T$
5. $(A^{\ast }{)}^{-1}=(A^{-1}{)}^{\ast }$
6. $A^{-k}=(A^{-1}{)}^k$
7. $A^0=E$
8. $|A^{-1}|=\frac{1}{|A|}$
9. 可逆矩阵可以表示成初等矩阵的乘积

三、乘法和逆矩阵

上一讲大概介绍了矩阵乘法和逆矩阵，本讲就来做进一步说明。

1.矩阵乘法

• 行列内积：有$m\times n$矩阵$A$和$n\times p$矩阵$B$（$A$的总列数必须与$B$的总行数相等），两矩阵相乘有$AB=C$，$C$是一个$m\times p$矩阵，对于$C$矩阵中的第$i$行第$j$列元素$c_{ij}$，有：

  $$c_{ij}=ro{w}_i\cdot colum{n}_j=\sum _{k=i}^n{a}_{ik}{b}_{kj}$$

  其中$a_{ik}$是$A$矩阵的第$i$行第$k$列元素，$b_{kj}$是$B$矩阵的第$k$行第$j$列元素。

  可以看出$c_{ij}$其实是$A$矩阵第$i$行点乘$B$矩阵第$j$列 $\left[\begin{array}{ccc}& ⋮& \\ & ro{w}_i& \\ & ⋮& \end{array}\right]\left[\begin{array}{ccc}& & \\ \cdots & colum{n}_j& \cdots \\ & & \end{array}\right]=\left[\begin{array}{ccc}& ⋮& \\ \cdots & c_{ij}& \cdots \\ & ⋮& \end{array}\right]$

• 整列相乘：上一讲我们知道了如何计算矩阵乘以向量，而整列相乘就是使用这种线性组合的思想：

  $\left[\begin{array}{cccc}& & & \\ A_{col1}& A_{col2}& \cdots & A_{coln}\\ & & & \end{array}\right]\left[\begin{array}{ccc}\cdots & b_{1j}& \cdots \\ \cdots & b_{2j}& \cdots \\ \cdots & ⋮& \cdots \\ \cdots & b_{nj}& \cdots \end{array}\right]=\left[\begin{array}{ccc}& & \\ \cdots & \left(b_{1j}{A}_{col1}+b_{2j}{A}_{col2}+\cdots +b_{nj}{A}_{coln}\right)& \cdots \\ & & \end{array}\right]$

  上面的运算为$B$的第$j$个列向量右乘矩阵$A$，求得的结果就是$C$矩阵的第$j$列，即$C$的第$j$列是$A$的列向量以$B$的第$j$列作为系数所求得的线性组合，$C_j=b_{1j}{A}_{col1}+b_{2j}{A}_{col2}+\cdots +b_{nj}{A}_{coln}$。

• 整行相乘：同样的，也是利用行向量线性组合的思想：

  $\left[\begin{array}{cccc}⋮& ⋮& ⋮& ⋮\\ a_{i1}& a_{i2}& \cdots & a_{in}\\ ⋮& ⋮& ⋮& ⋮\end{array}\right]\left[\begin{array}{ccc}& B_{row1}& \\ & B_{row2}& \\ & ⋮& \\ & B_{rown}& \end{array}\right]=\left[\begin{array}{c}⋮\\ \left(a_{i1}{B}_{row1}+a_{i2}{B}_{row2}+\cdots +a_{in}{B}_{rown}\right)\\ ⋮\end{array}\right]$

  上面的运算为$A$的第$i$个行向量左乘矩阵$B$，求得的结果就是$C$矩阵的第$i$行，即$C$的第$i$行是$B$的行向量以$A$的第$i$行作为系数所求的的线性组合，$C_i=a_{i1}{B}_{row1}+a_{i2}{B}_{row2}+\cdots +a_{in}{B}_{rown}$。

• 列乘以行：用$A$矩阵的列乘以$B$矩阵的行，得到的矩阵相加即可：

  $\left[\begin{array}{cccc}& & & \\ A_{col1}& A_{col2}& \cdots & A_{coln}\\ & & & \end{array}\right]\left[\begin{array}{ccc}& B_{row1}& \\ & B_{row2}& \\ & ⋮& \\ & B_{rown}& \end{array}\right]=A_{col1}{B}_{row1}+A_{col2}{B}_{row2}+\cdots +A_{coln}{B}_{rown}$

  注意，$A_{coli}{B}_{rowi}$是一个$m\times 1$向量乘以一个$1\times p$向量，其结果是一个$m\times p$矩阵，而所有的$m\times p$矩阵之和就是计算结果。

• 分块乘法：$\left[\begin{array}{cc}{A}_1& A_2\\ A_3& A_4\end{array}\right]\left[\begin{array}{cc}{B}_1& B_2\\ B_3& B_4\end{array}\right]=\left[\begin{array}{cc}{A}_1{B}_1+A_2{B}_3& A_1{B}_2+A_2{B}_4\\ A_3{B}_1+A_4{B}_3& A_3{B}_2+A_4{B}_4\end{array}\right]$
  在分块合适的情况下，可以简化运算。

• 矩阵运算需要注意的一些问题

一些结论：

1. $(E+A)(E-A)=(E-A)(E+A)=E-A^2$
2. $tr(AB)=tr(BA)$
3. 与所有$n$级矩阵可交换的矩阵(可交换指$AB$=$BA$)一定是$n$级数量矩阵
4. 可交换矩阵之间的运算符合平方差公式和二项式展开等公式，可以视为常数运算

2.逆（方阵）

首先，并不是所有的方阵都有逆；而如果逆存在，则有$A^{-1}A=E=A{A}^{-1}$。教授这里提前剧透，对于方阵，左逆和右逆是相等的，但是对于非方阵（长方形矩阵），其左逆不等于右逆。

对于这些有逆的矩阵，我们称其为可逆的或非奇异的。我们先来看看奇异矩阵（不可逆的）：$A=\left[\begin{array}{cc}1& 2\\ 3& 6\end{array}\right]$，在后面将要学习的行列式中，会发现这个矩阵的行列式为$0$。

观察这个方阵，我们如果用另一个矩阵乘$A$，则得到的结果矩阵中的每一列应该都是$\left[\begin{array}{c}1\\ 2\end{array}\right]$的倍数，所以我们不可能从$AB$的乘积中得到单位矩阵$E$。

另一种判定方法，如果存在非零向量$x$，使得$Ax=0$，则矩阵$A$不可逆。我们来用上面的矩阵为例：$\left[\begin{array}{cc}1& 2\\ 3& 6\end{array}\right]\left[\begin{array}{c}3\\ -1\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$。

证明：如果对于非零的$x$仍有$Ax=0$，而$A$有逆$A^{-1}$，则$A^{-1}Ax=0$，即$x=0$，与题设矛盾，得证。

现在来看看什么矩阵有逆，设$A=\left[\begin{array}{cc}1& 3\\ 2& 7\end{array}\right]$，我们来求$A^{-1}$。$\left[\begin{array}{cc}1& 3\\ 2& 7\end{array}\right]\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$，使用列向量线性组合的思想，我们可以说$A$乘以$A^{-1}$的第$j$列，能够得到$E$的第$j$列，这时我会得到一个关于列的方程组。

接下来介绍高斯-若尔当（Gauss-Jordan）方法，该方法可以一次处理所有的方程：

• 这个方程组为$\{\begin{array}{l}\left[\begin{array}{cc}1& 3\\ 2& 7\end{array}\right]\left[\begin{array}{c}a\\ b\end{array}\right]=\left[\begin{array}{c}1\\ 0\end{array}\right]\\ \left[\begin{array}{cc}1& 3\\ 2& 7\end{array}\right]\left[\begin{array}{c}c\\ d\end{array}\right]=\left[\begin{array}{c}0\\ 1\end{array}\right]\end{array}$，我们想要同时解这两个方程；

• 构造这样一个矩阵$\left[\begin{array}{cccc}1& 3& 1& 0\\ 2& 7& 0& 1\end{array}\right]$，接下来用消元法将左侧变为单位矩阵；

• $\left[\begin{array}{cccc}1& 3& 1& 0\\ 2& 7& 0& 1\end{array}\right]\stackrel{ro{w}_2-2ro{w}_1}{\to }\left[\begin{array}{cccc}1& 3& 1& 0\\ 0& 1& -2& 1\end{array}\right]\stackrel{ro{w}_1-3ro{w}_2}{\to }\left[\begin{array}{cccc}1& 0& 7& -3\\ 0& 1& -2& 1\end{array}\right]$

• 于是，我们就将矩阵从$\left[\begin{array}{cc}A& E\end{array}\right]$变为$\left[\begin{array}{cc}E& A^{-1}\end{array}\right]$

而高斯-若尔当法的本质是使用消元矩阵$E_{ij}$，对$A$进行操作，$E_{ij}\left[\begin{array}{cc}A& E\end{array}\right]$，利用一步步消元有$E_{ij}A=E$，进而得到$\left[\begin{array}{cc}E& A\end{array}\right]$，其实这个消元矩阵$E_{ij}$就是$A^{-1}$，而高斯-若尔当法中的$E$只是负责记录消元的每一步操作，待消元完成，逆矩阵就自然出现了。

四、$A$ 的 $LU$ 分解

$AB$的逆矩阵：
$$\begin{array}{rl}A\cdot A^{-1}=E& =A^{-1}\cdot A\\ (AB)\cdot (B^{-1}{A}^{-1})& =E\\ \text{则}AB\text{的逆矩阵为}& B^{-1}{A}^{-1}\end{array}$$

$A^T$的逆矩阵：
$$\begin{array}{rl}(A\cdot A^{-1}{)}^T& =E^T\\ (A^{-1}{)}^T\cdot A^T& =E\\ \text{则}{A}^T\text{的逆矩阵为}& (A^{-1}{)}^T\end{array}$$

将一个 $n$ 阶方阵 $A$ 变换为 $LU$ 需要的计算量估计：

1. 第一步，将$a_{11}$作为主元，需要的运算量约为$n^2$

$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]\underrightarrow{消元}\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ 0& a_{22}& \cdots & a_{2n}\\ 0& ⋮& \ddots & ⋮\\ 0& a_{n2}& \cdots & a_{nn}\end{array}\right]$$

2. 以此类推，接下来每一步计算量约为$(n-1{)}^2、(n-2{)}^2、\cdots 、2^2、1^2$。

3. 则将 $A$ 变换为 $LU$ 的总运算量应为$O(n^2+(n-1{)}^2+\cdots +2^2+1^2)$，即$O(\frac{n^3}{3})$。

置换矩阵(Permutation Matrix)：

3阶方阵的置换矩阵有6个：
$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]\left[\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]$$

$n$阶方阵的置换矩阵有$\left(\genfrac{}{}{0ex}{}{n}{1}\right)=n!$个。

五、转换、置换、向量空间R

1.置换矩阵（Permutation Matrix）与初等变换（Primary Transformations）

置换矩阵$P$的作用是交换行或列，而转置矩阵的作用是做转置操作$T$

$P$为置换矩阵，对任意可逆矩阵$A$有：

$PA=LU$

对置换矩阵$P$，有$P^{T}P=E$

即$P^T=P^{-1}$，即$P$是正交矩阵

初等变换包括初等列变换和初等行变换，初等行变换指：交换行；某行进行数乘；某行数乘后加到另一行，初等列变换不同的只是对列施加操作。初等变换对应的矩阵是初等矩阵，初等矩阵都可逆

2.转置矩阵（Transpose Matrix）

$(A^T{)}_{ij}=(A{)}_{ji}$

1. $(A^T{)}^T=A$
2. $(A+B{)}^T=A^T+B^T$ （重要）
3. ${(\lambda A)}^T=\lambda A^T$
4. $(AB{)}^T=B^T{A}^T$
5. $rank(A^{T}A)=rank(A)=rank(A^T)=rank(A{A}^T)$

3.对称矩阵（Symmetric Matrix）

$A^T$ = $A$

对任意矩阵$R$有$R^{T}R$为对称矩阵：
$$\begin{gathered} (R^{T}R{)}^T=(R{)}^T(R^T{)}^T=R^{T}R \\ \text{即}(R^{T}R{)}^T=R^{T}R \end{gathered}$$
对任意矩阵$A$，$A^{T}A$是对称半正定矩阵

4.线性空间（Linear Space）

本节的笔记来源 Mathor’s blog

线性空间是定义在数域$\mathbb{F}$上满足某些运算规律的向量集合，而数域本身也是一种特殊的集合。所以我们先讲数域，再讲线性空间

什么是数域？数域是一种数集，元素的和、差、积、商仍在数集中（具有封闭性），称为数域。如有理数域 $\mathbb{Q}$，复数域 $\mathbb{C}$，实数域$\mathbb{R}$，复数域包含实数域

线性空间的定义：

设 $V$ 是以 $\alpha ,\beta ,\gamma ,\cdots$ 为元素的非空集合，$\mathbb{F}$ 是一个数域，定义两种运算：加法 $\forall \alpha ,\beta \in V,\alpha +\beta \in V$；数乘 $\forall k\in \mathbb{F},\alpha \in V,k\alpha \in V$。满足 8 条：加法交换律、加法结合律、数乘结合律、两个分配律，零元 (单位元) 存在，1 (幺) 元存在，负元存在。则称 $V$ 为数域 $\mathbb{F}$ 上的线性空间

1. 交换律 $\alpha +\beta =\beta +\alpha$
2. 结合律 $\alpha +(\beta +\gamma )=(\alpha +\beta )+\gamma$
3. 零元素 在$V$中有一元素 $0$（称作零元素，注：该$0$ 为向量），对于 $V$中任一元素 $\alpha$ 都有 $\alpha +0=\alpha$
4. 负元素 对于$V$中每一个元素$\alpha$，都有 $V$中的元素 $\beta$，使得 $\alpha +\beta =0$，其中，$0$ 代表的是零元素，但不一定永远都是 $0$ 这个数，视具体题目而定
5. $\alpha ・1=\alpha$，其中$1$是数，不是向量
6. $(\alpha l)k=\alpha (kl)$
7. $\alpha (k+l)=\alpha k+\alpha l$
8. $(\alpha +\beta )k=\alpha k+\beta k$

$注：\alpha ,\beta ,\gamma \in V且1,k,l\in \mathbb{F}$

简单点说，上述 8 条，只要有任意一条不满足，则$V$就不是数域$\mathbb{F}$上的线性空间（线性空间中的元素叫向量）

例 1

V = { 0 } V=\{0\} V={0},$\mathbb{F}$ 是数域，判断 $V$ 是否为数域 $\mathbb{F}$ 上的线性空间

解：判断是否线性空间，只需要证明集合 $V$ 在数域 $\mathbb{F}$ 上是否满足上述 8 条。这里明显满足条件，因此 $V$ 是数域 $\mathbb{F}$ 上的线性空间

---

例 2

$R^{+}$ 表示所有正实数集合，在 $R^{+}$ 中定义加法 $\oplus$ 与数量乘法 $\odot$ 分别为

$a\oplus b=ab(\forall a,b\in R^{+})$

$k\odot a=a^k(\forall a\in R^{+},k\in \mathbb{R})$

判断 $R^{+}$ 是否构成实数域 $\mathbb{R}$ 上的线性空间

解：通过证明交换律，结合律，零元素，负元素，数乘结合律，两个分配律。因此 $R^{+}$ 是实数域 $\mathbb{R}$ 上的线性空间

• 交换律：$a\oplus b=ab=ba=b\oplus a$
• 结合律：$a\oplus (b\oplus c)=a(bc)=(ab)c=(a\oplus b)\oplus c$
• 零元素：这个比较复杂，我详细推导一下。原始定义中 $\alpha \oplus 0=\alpha$，因此 $0$ 就是零元素。但是对于这道题，我们需要找到一个数 $x$，使得 $a\oplus x=ax=a$，显然，$x=1$。因此，$R^{+}$ 存在零元素，零元素是 $1$
• 负元素：与零元素同理，原始定义中 $\alpha \oplus \beta =0$，因此 $\beta$ 就是 $\alpha$ 的负元素。对于这道题，我们需要找到一个数 $y$，使得 $\alpha \oplus y=\alpha y=0$。但是要注意，这里的 0 是零元素，而上面我们已经推出零元素是 1。所以这里我们需要证明的式子应该是 $\alpha \oplus y=\alpha y=1$，显然，$y=\frac{1}{\alpha }$，并且 $\alpha$ 是正实数集合中的元素，因此 $\alpha \ne 0$
• 数乘结合律：$k\odot (l\odot \alpha )=k\odot ({\alpha }^l)={\alpha }^{lk}={\alpha }^{kl}=(kl)\odot \alpha$
• 分配律 1：$(k+l)\odot \alpha ={\alpha }^{k+l}={\alpha }^k{\alpha }^l={\alpha }^k\oplus {\alpha }^l=(k\odot \alpha )\oplus (l\odot \alpha )$
• 分配律 2：$k\odot (\alpha \oplus \beta )=(\alpha \beta {)}^k={\alpha }^k{\beta }^k=(k\odot \alpha )\oplus (k\odot \beta )$

---

例 3

设 $V$ 是由系数在实数域 $\mathbb{R}$ 上，次数为 $n$ 的 $n$ 次多项式 $f(x)$ 构成的集合，其加法运算与数乘运算按照通常规定，举例说明 $V$ 不是 $\mathbb{R}$ 上的线性空间

解：$V$ 是由次数为 $n$ 的 $n$ 次多项式 $f(x)$ 构成的集合，显然加法不封闭。例如 $x\in V$，则 $x+(-x)=0$，$0$ 的次数不再是 $n$，次数下降，不再属于 $V$ 了。同理，数乘也不封闭。例如 $x\in V$，则 $x・0=0$，次数同样下降，不属于 $V$。因此 $V$ 不是 $\mathbb{R}$ 上的线性空间

---

线性空间的性质

• 加法零元 (单位元) 唯一

证：设 $0_1$,$0_2$ 是两个零元，则 $0_1=0_1+0_2=0_2+0_1=0_2$

• 加法负元唯一

证：设 $\alpha$ 的负元为 ${\beta }_1,{\beta }_2$，则 ${\beta }_1={\beta }_1+0=\beta 1+(\alpha +{\beta }_2)=({\beta }_1+\alpha )+{\beta }_2={\beta }_2$

・$\forall \alpha \in V,0・\alpha =0$，其中，第一个 $0$ 是数，第二个 $0$ 是向量

・$\forall k\in F,k・0=0$，其中的两个 $0$ 是相同的，都是向量

若 $k\alpha =0，则k=0或\alpha =0$

若 $\alpha +\beta =\alpha +\gamma ，则\beta =\gamma$

设 $V$ 是 $\mathbb{F}$ 上的线性空间，${\alpha }_1,{\alpha }_2,...,{\alpha }_p$ 和 ${\beta }_1,{\beta }_2,...,{\beta }_q$ 是 $V$ 中的两个向量组，$\beta \in V$

1. 如果存在 $p$ 个数 $k_i\in \mathbb{F},i=1,2,...,p$，使得 ${\alpha }_1{k}_1+{\alpha }_2{k}_2+・・・+{\alpha }_p{k}_p=\beta$，称向量 $\beta$ 可由向量组 ${\alpha }_1,{\alpha }_2,...,{\alpha }_p$ 线性表示
2. 如果每个 ${\beta }_j$ 都可以由向量组 ${\alpha }_1,{\alpha }_2,...,{\alpha }_p$ 线性表示，$j=1,2,...,q$。为了方便，${\beta }_1,{\beta }_2,...,{\beta }_q$ 可由 ${\alpha }_1,{\alpha }_2,...,{\alpha }_p$ 线性表示，用符号记为 { β 1 , β 2 , . . . , β q } ≤ l i n { α 1 , α 2 , . . . , α p } \{β_1,β_2,...,β_q\}≤_{lin}\{α_1,α_2,...,α_p\} {β1​,β2​,...,βq​}≤lin​{α1​,α2​,...,αp​}

---

线性表示关系的传递性

设 $V$ 是 $\mathbb{F}$ 上的线性空间，${\alpha }_1,{\alpha }_2,...,{\alpha }_p；{\beta }_1,{\beta }_2,...,{\beta }_q；{\gamma }_1,{\gamma }_2,...,{\gamma }_t$是 $V$ 中三个向量组。若

{ α 1 , α 2 , . . . , α p } ≤ l i n { β 1 , β 2 , . . . , β q } \{α_1,α_2,...,α_p\}≤_{lin}\{β_1,β_2,...,β_q\} {α1​,α2​,...,αp​}≤lin​{β1​,β2​,...,βq​}

{ β 1 , β 2 , . . . , β q } ≤ l i n { γ 1 , γ 2 , . . . , γ t } \{β_1,β_2,...,β_q\}≤_{lin}\{γ_1,γ_2,...,γ_t\} {β1​,β2​,...,βq​}≤lin​{γ1​,γ2​,...,γt​}

则 { α 1 , α 2 , . . . , α p } ≤ l i n { γ 1 , γ 2 , . . . , γ t } \{α_1,α_2,...,α_p\}≤_{lin}\{γ_1,γ_2,...,γ_t\} {α1​,α2​,...,αp​}≤lin​{γ1​,γ2​,...,γt​}

---

• 线性空间的基与坐标

• 基的引入将抽象线性空间内的问题转化为了代数问题，例如判断线性空间中的元素是否线性相关，只需要将这些元素转化为它们对应的坐标，再判断坐标是否线性相关即可

• 线性空间基变换和坐标变换

• 线性空间的直和

• 线性子空间相关例题

• 线性映射