R语言知识点整理

R概述

时间：1995年诞生

特点：

1. 免费，开源
2. R是解释性语言
3. R提供给了非常丰富的2D和3D图形库
4. 占用内存小，各种OS兼容性好
5. 资源丰富 社区强大

缺点：

1. 数据处理在内存中进行，不适于处理超大规模的数据
2. 运行速度慢，相当于C语言的1/20

基础操作

基本操作

> myString <- "hello R"
> myString
[1] "hello R"
> print(myString)
[1] "hello R"

基本命令

# 退出
q()
# 设置当前工作目录
setwd("path")
# 查看当前工作目录
getwd()
# 清空console
CTRL+L
# 中断当前计算
ESC
# 得到相应函数的帮助
help(plot)
# 得到R提供的几个示例
demo(colors),demo(lm.glm)

变量

变量命名

R语言的有效的变量名称由字母、数字及点号.或下划线组成；区分大小写

不能以数字开头；可以.开头；.开头不能跟数字；不能以下划线开头

变量赋值

# 等号赋值
> var.1 = c(0,1,2,3)
> var.1
[1] 0 1 2 3

> # 查看以创建的变量
> ls()
 [1] "a"                "ages"             "art"             
 [4] "Arthritis"        "chisq_result"     "cluster_labels"  
 [7] "cor_matrix"       "dat"              "dat_subset"      
[10] "data"             "data1"            "df"  

删除变量

> rm(a)

输出和输入

输出

# 使用print进行基本输出
> print("1, 加, 1,等于, 2,'\n'")
[1] "1, 加, 1,等于, 2,'\n'"
# 使用cat可进行拼接
> cat(1, "加", 1,"等于", 2,'\n')
1 加 1 等于 2 
cat函数会在每两个拼接元素之间自动加上空格
# cat()函数可以直接输出结果到文件
> cat("kyb", file='kyb.txt')

输入

# 读取房价数据
w = read.csv("ag.csv")
# 查看数据前几行，默认六行
head(w)

注释

# 单行注释
"
多行
注释
"

数学计算

> # 开根号
> sqrt(4)
[1] 2
> # e的n次方
> exp(1)
[1] 2.718282

> # 四舍五入取整
> round(5.1)
[1] 5
> round(5.5)
[1] 6

> # 向上取整与向下取整
> ceiling(3.1)
[1] 4
> floor(3.9)
[1] 3

# R的三角函数是弧度制
> sin(pi/6)
[1] 0.5
> cos(pi/2)
[1] 6.123032e-17
> tan(pi/4)
[1] 1

# 产生n个服从正态分布的随机数
> rnorm(3, mean = 0, sd = 1)
[1]  2.1988103  1.3124130 -0.2651451

数据结构

向量

因子

数组

矩阵

列表

数据框

特殊值数据

有用函数

向量(vector)

向量是用于存储数值型、字符型或逻辑型数据的一维数组

向量的创建

# 使用c()创建一个向量
> a = c(3,4)
> b = c(5,0)
> a
[1] 3 4
> b
[1] 5 0

R语言的向量的下标是从1开始的。

> a[1]
[1] 3
> b[2]
[1] 0

> a + b
[1] 8 4
# 这里把两个二维向量相加，得到一个新的二维向量(8,4)
# 若将一个二维向量和三维向量做运算，则会失去数学意义

可以用c()创建向量；也可以用min:max生成连续的序列；也可使用seq函数生成有间隙的等差数列

# 使用`min:max`生成连续的序列
> a = c(1:5)
> a
[1] 1 2 3 4 5

# 使用seq创建等差序列
# 创建一个从1到9，间隔为2的等差序列
> seq(1,9,2)
[1] 1 3 5 7 9
# 步长为-20的[0, 100]之间的等差递减数列
> seq(100, 0, -20)
[1] 100  80  60  40  20   0

# seq()生成等比数列
# 10为首项，2为公比的等比序列
> i = seq(1,4,1)
> a = 5
> y = a*2^i
> y
[1] 10 20 40 80
# 使用rep重复元素创建向量
> a = rep(0,3)
> a
[1] 0 0 0
# 产生字母序列letters
> letters[1:26]
 [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n"
[15] "o" "p" "q" "r" "s" "t" "u" "v" "w" "x" "y" "z"

向量的运算

# 向量支持标量计算
> c(1,2,3) - 0.5
[1] 0.5 1.5 2.5
# 向量中可以使用的统计学函数
# 求和sum
> a
[1] 3 4
> sum(a)
[1] 7
# 求平均mean
> mean(a)
[1] 3.5
# 求方差 var
> var(a)
[1] 0.5
# 求标准差 sd
> sd(a)
[1] 0.7071068
# 求最大最小值
> min(a)
[1] 3
# 取值范围
> a = c(1,2,3,4,5)
> range(a)
[1] 1 5
# 元素提取
# 直接根据下标取值
> a = c(1,2,3,4)
> a[1]
[1] 1
# 向量删除
# 删除向量第一个元素
> a = c(1,2,3,4,5,6,7,8,9,10)
> a
 [1]  1  2  3  4  5  6  7  8  9 10
> a[-1]
[1]  2  3  4  5  6  7  8  9 10
# 删除向量中第一个第三个元素
> a = c(1,2,3,4,5,6,7,8,9,10)
> b = c(1,3)
> a[-b]
[1]  2  4  5  6  7  8  9 10
# 向量更新
# 在向量a的第i个位置插入新数据y
> a = 2:6
> a
[1] 2 3 4 5 6
> a1 <- c(a[1:2],99,a[3:6])
> a1
[1]  2  3 99  4  5  6 NA
# 修改向量
# 第i的位置的数据修改为y
> a <- 2:6
> a
[1] 2 3 4 5 6
> a[5] <- 22
> a
[1]  2  3  4  5 22
# 向量排序1——sort()
sort(x, decreasing=FALSE/TRUE,...) 升序/降序
> b <- c(1,6,3,8,2,4,5,7,3,7,1,3)
> b
 [1] 1 6 3 8 2 4 5 7 3 7 1 3
> sort(b)
 [1] 1 1 2 3 3 3 4 5 6 7 7 8
> b
 [1] 1 6 3 8 2 4 5 7 3 7 1 3
# 可以看到sort()默认是升序排序，且sort()不会改变源列表
# decreasing = TRIE为降序
> c = sort(b, decreasing = TRUE)
> c
 [1] 8 7 7 6 5 4 3 3 3 2 1 1

# 向量排序2——order
# order函数指出排序后的向量中各元素在原向量中的索引，默认升序
> a <- c(3.99, 5.99, 2.99, 1.99)
> b <- c("apple", "orange", "banana", "pear")
> b[order(a)]
[1] "pear"   "banana" "apple"  "orange"
#示例代码中，向量a和向量b的元素分别表示商品价格和商品名称，使用order()函数获取向量a中元素升序排列的位置向量，然后根据该位置向量对向量b进行重新排序，最终得到按照价格排序后的商品名称向量。

# rank()函数用于获取向量或矩阵中每个元素的排名
> x <- c(3, 2, 5, 2, 1, 6)
> rank(x)
[1] 4.0 2.5 5.0 2.5 1.0 6.0
# 这个结果表示向量x中最小的元素1排名为第2，次小的元素2排名为第3和第4，以此类推，最大的元素6排名为第6。

# 向量逆转 rev
> b = 1:5
> b
[1] 1 2 3 4 5
> rev(b)
[1] 5 4 3 2 1
> b
[1] 1 2 3 4 5
# 可以看到rev函数不改变原数组

# 删除缺失值 na.omit(c)
> d <- c(3,9,2,NA,6,5)
> d
[1]  3  9  2 NA  6  5
> length(d)
[1] 6
> # 判断是否为缺失值
> d == 'NA'
[1] FALSE FALSE FALSE    NA FALSE FALSE
> e <- na.omit(d)
> e
[1] 3 9 2 6 5

# 筛选——which
> a <-c(2,3,4,2,5,6,7,9,6,2,1,3)
> which.max((a))# 返回下标
[1] 8
> a[8] # 根据下标取出最大值
[1] 9
> a[which.max(a)]
[1] 9
> # 取出大于5的元素
> a[which(a>5)]
[1] 6 7 9 6
> # 取出a中不等于3的元素
> a[which(a!=3)]
 [1] 2 4 2 5 6 7 9 6 2 1

向量中的空

NA代表的是缺失(missing value)NA确实就像占位符，代表这里没有值，但是位置存在

NULL代表就是空值，数据不存在

NaN表示非数值，not a number

inf：表示无穷大

> length(c(NA,NA,NULL))
[1] 2
> c(NA,NA,NULL,NA)
[1] NA NA NA

矩阵

矩阵的创建

# 矩阵是一个二维数组，每个元素都拥有相同的模式(数值型、字符型或逻辑型)
mymatrix <- matrix(vector, nrow=number_of_rows, ncol=number_of_columns,
                  byrow=logical_value,
                  dimnames=list(char_vector_rownames, 
                   char_vector_colnames))
# vector包含了矩阵的元素，nrow和ncol用以指定行和列的维数
# byrow是设定矩阵应当按行填充(byrow=TRUE)还是按列填充(byrow=FALSE),默认按列
> # 生成向量
> cells <- c(1,26,14,68)
> rnames <- c('R1','R2')# 定义列名
> cnames <- c('C1',"c2")# 定义行名
> mymatrix <- matrix(cells, nrow = 2, ncol = 2, byrow = TRUE,dimnames=list(rnames, cnames))
> mymatrix
   C1 c2
R1  1 26
R2 14 68
> # 通过matrix创建一个3x4的矩阵
> m <- matrix(1:12, nrow = 3, ncol = 4)
> m
     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

$$\left[\begin{array}{cccc}1& 4& 7& 10\\ 2& 5& 8& 11\\ 3& 6& 9& 12\end{array}\right]$$

# 矩阵生成方式二
> # 生成向量1
> x1 <- c(2,4,6,8)
> # 生成向量2
> x2 <- c(1,3,7,9)
> # 按行生成矩阵
> rbind(x1,x2)
   [,1] [,2] [,3] [,4]
x1    2    4    6    8
x2    1    3    7    9
> # 按列生成矩阵
> cbind(x1,x2)
     x1 x2
[1,]  2  1
[2,]  4  3
[3,]  6  7
[4,]  8  9

矩阵的运算

# 矩阵数据的选择
> y
     [,1] [,2]
[1,]    1    6
[2,]    2    7
[3,]    3    8
[4,]    4    9
[5,]    5   10
> # 矩阵的第一行
> y[1,]
[1] 1 6
> # 矩阵的第一列
> y[,1]
[1] 1 2 3 4 5
> # 矩阵的第一行第二个元素
> y[1,2]
[1] 6

# 选择多行或多列时，下标i和j可为数值型向量
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    3    5    7    9
[2,]    2    4    6    8   10
> x[1,c(4,5)]
[1] 7 9
> x[1,4:5]
[1] 7 9
############################################################################
# 矩阵转置 t()
> x
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    3    5    7    9
[2,]    2    4    6    8   10
> t(x)
     [,1] [,2]
[1,]    1    2
[2,]    3    4
[3,]    5    6
[4,]    7    8
[5,]    9   10

数组

数组(array)与矩阵类似，但是维度可以大于2

数组通过array创建，形式如下：

myarray <- array(vector, dimensions, dimnames)
# vector包含了数组中的数据，dimensions是一个数值型向量，给出了各个维度下标的最大值
dimnames是可选的、各维度名称标签的列表

数组的创建

# 使用runif生成12个服从均匀分布的随机数，生成四行三列的数组
> x <- array(runif(12), c(4,3))
> x
             [,1]      [,2]      [,3]
[1,] 0.7544751586 0.4753166 0.3517979
[2,] 0.6292211316 0.2201189 0.1111354
[3,] 0.7101824014 0.3798165 0.2436195
[4,] 0.0006247733 0.6127710 0.6680556

# 创建两个两行三列的数组
> x <- array(runif(12), c(2,3,2))
> x
, , 1

          [,1]      [,2]      [,3]
[1,] 0.4176468 0.1028646 0.9849570
[2,] 0.7881958 0.4348927 0.8930511

, , 2

          [,1]      [,2]      [,3]
[1,] 0.8864691 0.1306957 0.3435165
[2,] 0.1750527 0.6531019 0.6567581
#######################################################
> dim1 <- c("A1","A2")
> dim2 <- c("B1","B2","B3")
> dim3 <- c("C1","C2","C3","C4")
# 这三个dim分别是行，列，个数的名称
> z <- array(1:24, c(2,3,4), dimnames = list(dim1,dim2,dim3))
> z
, , C1

   B1 B2 B3
A1  1  3  5
A2  2  4  6

, , C2

   B1 B2 B3
A1  7  9 11
A2  8 10 12

, , C3

   B1 B2 B3
A1 13 15 17
A2 14 16 18

, , C4

   B1 B2 B3
A1 19 21 23
A2 20 22 24

数组的运算

# 数组取值
> x <- array(data = c(1,2,3,4,5,6), c(2,3))
> x
     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6
> x[1,]
[1] 1 3 5
> # 取列
> x[,1]
[1] 1 2
> # 取一行两列
> x[1,2]
[1] 3

数据框

数据框的数据可以有多种数据类型，而向量，矩阵和数组只能包含一种数据类型

数据框每一列的数据类型是唯一的

R语言数据框使用data,frame()函数来创建，语法格式如下：

data.frame(..., row.names = NULL, check.rows = FALSE,
          check.names = TRUE, fix.empty.names = TRUE,
          stringsAsFactors = default.stringAsFactors())

...:列向量，可以是任何类型（字符型、数值型、逻辑型），一般以 tag = value 的形式表示，也可以是 value。

row.names: 行名，默认为 NULL，可以设置为单个数字、字符串或字符串和数字的向量。

check.rows: 检测行的名称和长度是否一致。

check.names: 检测数据框的变量名是否合法。

fix.empty.names: 设置未命名的参数是否自动设置名字。

stringsAsFactors: 布尔值，字符是否转换为因子，factory-fresh 的默认值是 TRUE，可以通过设置选项（stringsAsFactors=FALSE）来修改。

创建数据框

> table <- data.frame(
+     "姓名" = c("张三", "李四"),
+     "工号" = c("001","002"),
+     "月薪" = c(1000,2000)
+ )
> table
  姓名 工号 月薪
1 张三  001 1000
2 李四  002 2000
2 李四  002 2000
############################################################
> # 病人ID
> patientID <- c(1,2,3,4)
> age <- c(25,34,28,52)
> diabets <- c("Type1", "Type2", "Type1", "Type1")
> status <- c("Poor", "Improved", "Excellent", "Poor")
> patientdata <- data.frame(patientID, age, diabets, status)
> patientdata
  patientID age diabets    status
1         1  25   Type1      Poor
2         2  34   Type2  Improved
3         3  28   Type1 Excellent
4         4  52   Type1      Poor

数据框的使用

> patientdata
  patientID age diabets    status
1         1  25   Type1      Poor
2         2  34   Type2  Improved
3         3  28   Type1 Excellent
4         4  52   Type1      Poor
_____________________________________________
> # 显示前两列数据
> patientdata[1:2]
  patientID age
1         1  25
2         2  34
3         3  28
4         4  52
_____________________________________________
> # 显示特定列名的列
> patientdata["status"]
     status
1      Poor
2  Improved
3 Excellent
4      Poor
_____________________________________________
> patientdata[c("patientID","status")]
  patientID    status
1         1      Poor
2         2  Improved
3         3 Excellent
4         4      Poor
########################################################
# 提取元素
> patientdata
  patientID age diabets    status
1         1  25   Type1      Poor
2         2  34   Type2  Improved
3         3  28   Type1 Excellent
4         4  52   Type1      Poor
> # 显示前两列数据
> patientdata[1:2]
  patientID age
1         1  25
2         2  34
3         3  28
4         4  52
> # 显示特定列名的列
> patientdata["status"]
     status
1      Poor
2  Improved
3 Excellent
4      Poor
> # 显示多列
> patientdata[c(patientID,"status")]
Error in `[.data.frame`(patientdata, c(patientID, "status")) : 
  选择了未定义的列
> patientdata[c("patientID","status")]
  patientID    status
1         1      Poor
2         2  Improved
3         3 Excellent
4         4      Poor
########################################################
# 提取元素生成列联表
> # 生成糖尿病类型变量diabetes和病情变量status的列联表(table)
# 记号$是被用来选取一个给定数据框中的某个特定变量
> table(patientdata$diabets, patientdata$status)
       
        Excellent Improved Poor
  Type1         1        0    2
  Type2         0        1    0

因子

类别（名义型）变量和有序类别（有序型）变量在R中称为因子（factor）。

# 函数factor()用来把一个向量编码成为一个因子
# 一般形式为：
factor(x, levels=sort(unique(x), na.list = TRUE), labels, exclude=NA,
       order=FALSE)
# levels:可以自行指定各离散值取值，不指定时由x的不同值来求得[有序变量]
# labels：可以用来指定各水平的标签，不指定时用各离散取值的对应字符串dang
# exclude：参数用来指定要转换为缺失值(NA)的元素值集合。 
# ordered：取真值时表示因子水平是有次序的
可以用is.factor()检验对象是否是因子，用as.factor()把一个向量转换成一个因子

> gender <- c("Male", "Female", "Male", "Female", "Male", "Male", "Female")
> # 使用`factor`函数将其转化为一个因子：”
> gender_factor <- factor(gender)
> # 转化后的`gender_factor`因子对象包含了性别变量的所有取值以及对应的数字编码(称为水平)。可以通过`levels`函数查看因子的水平
> levels(gender_factor)
[1] "Female" "Male" 
# 因子在数据分析中的作用非常重要，因为它们可以用来表示分类变量，并且可以直接用于数据可视化和建模分析中。例如，我们可以用因子作为分类变量在图表中绘制直方图或者箱线图，或者将因子用于构建分类变量的逻辑回归模型。

列表

在 R 语言中，列表（list）是一种灵活的数据结构，可以用于存储不同类型的数据对象。列表可以包含向量、矩阵、数组、数据框、甚至是其他列表等多种类型的数据对象，因此被广泛应用于数据分析和编程中。

列表的创建

创建列表使用list函数

> mylits <- list("apple", c(1,2,3))
> mylits
[[1]]
[1] "apple"

[[2]]
[1] 1 2 3
####################################
# 本例创建的列表中有四个成分，一个字符串、一个数值型向量、一个矩阵以及一个字符型向量
> # 一个字符串
> g <- "my first list"
> # 一个向量
> h <- c(25,34,12,6)
> # 一个矩阵
> j <- matrix(1:10, nrow = 5)
> k <- c("孔","源","博")
> mylist <- list(title=g, ages=h, j, k)
> mylist
$title
[1] "my first list"

$ages
[1] 25 34 12  6

[[3]]
     [,1] [,2]
[1,]    1    6
[2,]    2    7
[3,]    3    8
[4,]    4    9
[5,]    5   10

[[4]]
[1] "孔" "源" "博"

列表中的访问

可以使用[[i]]或$name的方式来访问列表中的元素，其中i表示要访问元素的位置，name表示要访问的元素的名称

> mylist[[2]]
[1] 25 34 12  6
> mylist$title
[1] "my first list"

基本程序设计

1. 分支：if, else, if else, switch
2. 循环：for, while, repeat, break, next
3. 替代：apply， lapply， sapply， tapply， sweep

# if语句
> x <- 3
> if(x > 0){
+     print('x=3')
+ }
[1] "x=3"
########################if-else 语句的示例
> if(x<0){
+     print("x小于0")
+ }else{
+     print("x大于0")
+ }
[1] "x大于0"
###################if-else if-else
> x <- 8
> if(x<0){
+     print("x是负的")
+ }else if(x==0){
+     print("x等于0")
+ }else{
+     print("x是正的")
+ }
[1] "x是正的"
###################switch语句
> x <- "b"
> switch(x, 
+        "a"={
+            print("option A")
+        },
+        "b"={
+            print("option B")
+        },
+        "c"={
+            print("option C")
+        }
+        )
[1] "option B"
####################################循环
> total <- 0
> for (i in 1:100) {
+     total <- total + i
+ }
> total
[1] 5050
################################apply
# apply系列函数的基本作用是对数组(array,可以是多维)或者列表(list)按照元素或元素构成的子集合进行迭代，并将当前元素或子集作为参数调用某个指定函数。
apply(X, MARGIN, FUN, ...)
X表示要操作的数据；MARGIN表示要操作的维度，如果要对每一行进行操作，则设置为1；如果要对每一列进行操作，则设置为2；如果要对整个矩阵或数组进行操作，则设置为c(1,2)或者用all指定；FUN表示要执行的函数，可以是R语言中已有的函数，也可以是用户自定义的函数；...表示传递给FUN函数的参数。
apply()函数的返回值是一个向量、矩阵或数组。
> # 使用apply函数对矩阵进行操作，求每行的平均值
> m <- matrix(c(1:9), nrow = 3)
> apply(m, 1, mean)
[1] 4 5 6
###############按列
> m
     [,1] [,2] [,3]
[1,]    1    4    7
[2,]    2    5    8
[3,]    3    6    9
> # 计算列和
> apply(m,2,sum)
[1]  6 15 24


#########################函数编写
# 定义一个函数f(1)
> f1 <- function(x){
+     x^2
+ }
> f1(1)
[1] 1
> f1(3)
[1] 9

描述统计

描述性统计分析要对调查总体所有变量的有关数据进行统计性描述，主要包括数据的频数分析、集中趋势分析、离散程度分析、分布以及一些基本的统计图形

常用统计量

1. 参数
2. 统计量：根据样本数据计算出来的一个量。

常见汇总统计量

位置统计量：反映数据集中程度的统计量

1. 样本均值
2. 样本中位数
3. 极差

常见的汇总统计量

1. 样本的α分位数
2. 四分位间距
3. 样本标准差
4. 中位数绝对差

基本统计方法

基本统计计算

抽样

命令为sample，语法结构如下：

sample(x, size, replace=FALSE, prob=NULL)

• x: 用于抽样的向量。

• size: 指定要抽取的样本大小。

• replace: 一个逻辑值，用于指定是否进行有放回的抽样，默认值为 FALSE，表示进行无放回的抽样。

• prob: 一个可选的数值向量，用于指定每个元素被选中的概率。如果不指定，则默认为等概率抽样。

• > x <- c(1,2,3,4,5)
  > # 从向量x中进行无放回的抽样，抽取大小为3
  > sample(x, size = 3, replace = FALSE)
  [1] 4 1 5
  

R基础统计功能

> marks <- c(10,6,4,7,8)
> # 计算均值
> mean(marks)
[1] 7
> # 计算标准差
> sd(marks)
[1] 2.236068
> # 计算中位数
> median(marks)
[1] 7
> # 计算最小值
> min(marks)
[1] 4
> # 计算最大值
> max(marks)
[1] 10
> # 打印基本描述性统计分析
> summary(marks)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
      4       6       7       7       8      10 
> # 绘制箱线图
> boxplot(marks)

相关性

相关系数可以用来描述定量变量之间的关系。相关系数的符号(±)表明关系的方向(正方向或负方向)，其值的大小表示关系的强弱关系**(完全不相关时为0， 完全相关时为1)**

1. cor()计算各类相关系数
2. pcor()函数计算偏相关系数
3. cor.test()函数对单个的Pearson、spearman和Kendall相关系数进行检验

# cor()
cor(x, y, method = "pearson") # 可选Pearson，spearman，Kendall
###########################################################
> # 创建数据框，包含两个数值型变量
> df <- data.frame
> df <- data.frame(x = c(1,2,3,4,5), y=c(6,7,8,9,10))
> df
  x  y
1 1  6
2 2  7
3 3  8
4 4  9
5 5 10
> # 计算Pearson相关系数和p值
> cor.test(df$x, df$y, method = "pearson")

	Pearson's product-moment correlation

data:  df$x and df$y
t = 82191237, df = 3, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 1 1
sample estimates:
cor 
  1 

这是对两个数值型变量 df$x 和 df$y 进行 Pearson 相关性分析的结果。下面对每个部分进行解释：

data: df$x and df$y：表明所分析的数据是 df$x 和 df$y 这两个向量。
t = 82191237 和 df = 3：t 值为 82191237，自由度为 3，用于计算 p 值。
p-value < 2.2e-16：p 值小于 2.2e-16，表示在零假设（即 df$x 和 df$y 之间不存在线性关系）成立的情况下，观察到这样极端的相关性的概率极小，因此拒绝零假设，接受备择假设（即 df$x 和 df$y 之间存在线性关系）。
alternative hypothesis: true correlation is not equal to 0：备择假设为 df$x 和 df$y 之间的真实相关系数不等于 0。
95 percent confidence interval: 1 1：给出了 95% 置信区间的下界和上界，表示真实相关系数的值有 95% 的概率位于这个区间内，这里的区间为 [1, 1]，说明 df$x 和 df$y 之间存在一个完美的正相关关系。
sample estimates: cor 和 1：表明样本相关系数的值为 1，即完美的正相关关系。
综上，此结果表明 df$x 和 df$y 之间存在一个完美的正相关关系，这种关系是显著的，并且可以在统计上进行证明。

psych包中提供的corr.test( )函数可以一次做更多事情。corr.test()函数可以为Pearson、Spearman或Kendall相关计算相关矩阵和显著性水平。

> mydata <- data.frame(age=c(25,30,35,40,45),
+                      income=c(50000,60000,70000,80000,90000),
+                      education=c(12,14,16,18,20))
> # 使用corr.,test()计算Pearson相关系数和p值
> corr_matrix <- corr.test(mydata, method = "pearson")
> # 打印相关系数矩阵和显著性水平
> corr_matrix
Call:corr.test(x = mydata, method = "pearson")
Correlation matrix 
          age income education
age         1      1         1
income      1      1         1
education   1      1         1
Sample Size 
[1] 5
Probability values (Entries above the diagonal are adjusted for multiple tests.) 
          age income education
age         0      0         0
income      0      0         0
education   0      0         0

 To see confidence intervals of the correlations, print with the short=FALSE option

这是使用 corr.test() 函数计算 Pearson 相关系数和 p 值的结果。下面对每个部分进行解释：
Call:corr.test(x = mydata, method = "pearson")：这是 corr.test() 函数的调用，指定了要分析的数据 mydata 和所需的相关系数类型为 Pearson 相关系数。
Correlation matrix：相关系数矩阵，显示了 age、income 和 education 三个变量之间的 Pearson 相关系数。在这个例子中，所有变量之间的相关系数都是 1，说明它们是完全相关的。
Sample Size：样本大小，表示在计算相关系数时使用的样本量，这里是 5。
Probability values：p 值，显示了各个变量之间相关性的显著性水平，这些值都小于 0.05，说明它们之间的相关性是显著的。
Entries above the diagonal are adjusted for multiple tests.：因为在计算相关系数矩阵时，对多重检验进行了校正，所以相关系数矩阵上对角线上方的值被调整过，这是一种控制错误发现率的方法。
To see confidence intervals of the correlations, print with the short=FALSE option：如果想要查看相关系数的置信区间，可以将 corr.test() 函数的 short 参数设置为 FALSE，再次运行函数即可。
综上，这个例子中的相关性分析结果表明，age、income 和 education 这三个变量之间是完全相关的，它们之间的相关性是显著的。        

独立性检验/卡方检验

根据频数判断两类因子彼此相关或相互独立的假设检验。

chisq.test

独立性检验本身就是用来判断变量之间相关性的方法，如果两个变量彼此独立，那么两者统计上就是不相关的

> library(vcd)# 调用vcd
# 载入需要的程辑包：grid
> # 展示数据
> head(Arthritis)
  ID Treatment  Sex Age Improved
1 57   Treated Male  27     Some
2 46   Treated Male  29     None
3 77   Treated Male  30     None
4 17   Treated Male  32   Marked
5 36   Treated Male  46   Marked
6 23   Treated Male  58   Marked
> mytable <- xtabs(~Treatment+Improved, data = Arthritis) # 选取治疗情况和改善情况生成列联表
> chisq.test(mytable) # 卡方检验

	Pearson's Chi-squared test

data:  mytable
X-squared = 13.055, df = 2, p-value = 0.001463
X-squared = 13.055, df = 2, p-value = 0.001463：卡方检验结果，包括卡方统计量（X-squared）、自由度（df）和 p 值（p-value）。在本例中，卡方统计量为 13.055，自由度为 2，p 值为 0.001463。p 值小于显著性水平 0.05，说明治疗情况和改善情况之间存在显著的关联性。
综上，该卡方检验表明治疗情况和改善情况之间存在显著的关联性，即治疗情况对改善情况有一定的影响。

基础数据处理

1. R区分大小写

2. 这些度量或特征称为变量(variable)，变量称为特征(feature)，它们的取值称为观测值(observation)

   

3. 统计数据的分类

   1. 按计量层次：分类的数据(性别等)；顺序的数据(一等二等)；数值型数据(身高180，175等)
   2. 按收集方法：观察的数据；试验的数据
   3. 按时间状况：截面的数据(2022年我国各地区的国内生产总值数据)；时序的数据(1996~2022年国内生产总值)

4. 数据获取

   1. 第一手数据：人工收集的调查数据和试验数据、对自然和社会的观察数据、各个机构和企业的上报数据等
   2. 第二手数据：第二手数据是指在第一手数据基础上经过加工、整理、转换、筛选等处理后得到的数据

基础数据管理

vector 向量
numeric 数值型向量
logical 逻辑性向量
character 字符型向量
list 列表
data.frame 数据框
c 连接为向量或列表
length 求长度
subset 求子集
seq, from:to, sequence 等差序列
rep 重复
NA 缺失值
NULL 空对象
sort, order, unique, rev 排序
attr, attributes 对象属性
class 元素类型
mode, typeof 对象存储模式与类型
names 对象的名字属性

字符串处理

character 字符型向量
nchar 字符数
substr 取子串
format, formaC 把对象用格式转换为字符串
paste, strsplit 连接或拆分
charmatch pmach 字符串匹配
grep sub gsub 模式匹配与替换

复数

complex Re Im Mod Arg Conj 复数函数

因子

factor 因子
codes 因子的编码
levels 因子的各水平的名字
nlevels 因子的水品个数
cut 把数值型对象分区间转换为因子
table 交叉频数表
split 按因子分组
aggregate 计算各数据子集的概括统计量
tapply 对不规则数组应用函数

常用运算符

# 数学运算
+ - * / /\(小箭头，次幂)
# 比较运算
>,<,<=,>=,==,!=
# 逻辑运算 与 或 非
!, &, &&, |, ||
# 取整取余等
%/%  取整
%%   取余
# 判断a是否为b中的元素
a%in%b

可视化

• plot()——绘制图像

• plot(<vecter_horizontal>, <vector_vertical>, pch=as.integer()，col，xlab，ylab)——用factors区分图像点的类型pch（圆的，三角，叉），col是颜色类别，xlab或者ylab对应横纵轴标题

• coplot(y~x|a+b)——多个变量时的散点图，在a，b（向量或是因子）的划分下的y与x的散点图

• persp(，expand=0.2）——创建3D图，expand扩展值设置为0.2，否则为全屏扩展

• hist()——绘制直方图，体现样本分布情况

• barplot()——绘制柱状图，vector可增加名称。也可以绘制直方图，和hist（）均分数据不太一样， 需要用table（）统计各个子分段下样本数量后在画图。

• mosaicplot（x~y，main，color=T，xlab，ylab）——柱形对应关系图

• image（volcano）——加载栅格（矩阵）图像

散点图

散点图使用plot()函数来绘制

plot(x, y, type = "p", main = "Main Title", xlab = "X Label"
     ,ylab = "Y Label", col = "blue"
     , pch = 19, lty = 1, lwd = 1)

• x: 横坐标 x 轴的数据集合
• y: 纵坐标 y 轴的数据集合
• type：绘图的类型，p 为点、l 为直线， o 同时绘制点和线，且线穿过点。
• main: 图表标题。
• xlab、ylab: x 轴和 y 轴的标签名称。
• xlim、ylim: x 轴和 y 轴的范围。
• axes: 布尔值，是否绘制两个 x 轴。
• pch:指定散点的样式
• lty:指定线条的样式
• lwd:指定线条的宽度

type 参数可选择值：

• p：点图

• l：线图

• b：同时绘制点和线

• c：仅绘制参数 b 所示的线

• o：同时绘制点和线，且线穿过点

• h：绘制出点到横坐标轴的垂直线

• s：阶梯图，先横后纵

• S：阶梯图，先纵后竖

• n： 空图

• x <- c(1, 2, 3, 4, 5)
  y <- c(2, 4, 6, 8, 10)
  plot(x, y)
  

plot(x, y, pch = 19, col = "red", cex = 2)

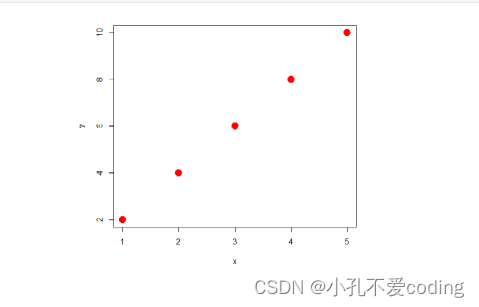
盒形图

> data = read.csv('ag.csv')
> plot(sell~reg,data)
> boxplot(sell~reg,data,main='123',xlab = 'x',ylab = 'y')

柱状图

R使用hist()函数创建直方图。 该函数将一个向量作为输入，并使用一些更多的参数绘制直方图。

hist(v, main,xlab,xlim,ylim,breaks,col,border)

•v - 包含直方图中使用数值的向量

•main - 表示图表的标题

•col - 用于设置条的颜色。

•border - 用于设置每个栏的边框颜色。

•xlab - x轴标签。

•xlim - 用于指定x轴上的值范围。

•ylim - 用于指定y轴上的值范围。

•breaks - 是用来提及每个栏的宽度。

> # 生成一组随机数据
> x <- rnorm(1000)
> # 绘制直方图
> hist(x, breaks = 20, col = 'blue', xlab = 'values', main = 'hist',ylab = 'Y')

条状图

使用barplot()函数来创建条形图，格式如下：

barplot(H, xlab, ylab, main, names.org, clo, beside)

• H 向量或矩阵，包含图表用的数字值，每个数值表示矩形条的高度。
• xlab x 轴标签。
• ylab y 轴标签。
• main 图表标题。
• names.arg 每个矩形条的名称。
• col 每个矩形条的颜色。
• beside=FALSE 时，条形图的高度是矩阵的数值，矩形条是水平堆叠的。
• beside=TRUE 时，条形图的高度是矩阵的数值，矩形条是并列的。

> df <- data.frame(city=c("Beijing", "Shanghai", "Guangzhou"), sales=c(200, 300, 250))
> barplot(df$sales, names.arg=df$city, main="Sales by City", xlab="City", ylab="Sales", col=c("red", "blue", "green"), ylim=c(0, 350))

> text(x=1:3, y=df$sales+10, labels=df$sales, pos=3)

• height: 每个城市的销售额数据，也可以使用数据框的方式传入。
• names.arg: x轴标签，也就是城市名称。
• main: 图表标题。
• xlab: x轴标签。
• ylab: y轴标签。
• col: 每个柱子的填充颜色。
• ylim: y轴的范围。

在图表上添加标题、颜色及每个矩形条的名称

> cvd19 = c(83534,2640626,585493)
> 
> barplot(cvd19,
+         main="新冠疫情条形图",
+         col=c("#ED1C24","#22B14C","#FFC90E"),
+         names.arg=c("中国","美国","印度")
+ )
Hit <Return> to see next plot: 

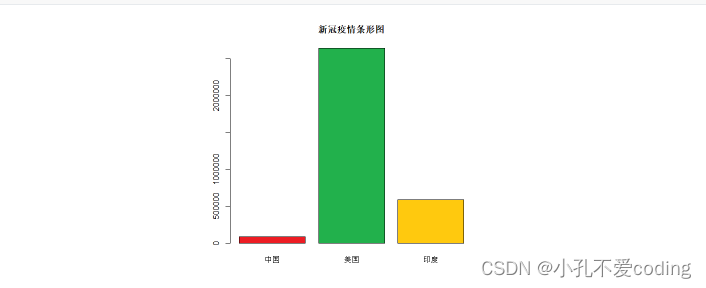
barplot中的数据既可以是向量，也可以是矩阵

cvd19 = matrix(
  c(83017, 83534, 1794546, 2640626, 190535, 585493),
  2, 3
)

colnames(cvd19) = c("中国", "美国", "印度")
rownames(cvd19) = c("6月", "7月")

barplot(cvd19, main = "新冠疫情条形图", beside=TRUE, legend=TRUE,col=c("blue","green"))

将beside参数改为FALSE

饼图

使用pie()函数来实现饼图

pie(x, labels = names(x), edges = 200, radius = 0.8,
    clockwise = FALSE, init.angle = if(clockwise) 90 else 0,
    density = NULL, angle = 45, col = NULL, border = NULL,
    lty = NULL, main = NULL, …)

• x: 数值向量，表示每个扇形的面积。
• labels: 字符型向量，表示各扇形面积标签。
• edges: 这个参数用处不大，指的是多边形的边数（圆的轮廓类似很多边的多边形）。
• radius: 饼图的半径。
• main: 饼图的标题。
• clockwise: 是一个逻辑值,用来指示饼图各个切片是否按顺时针做出分割。
• angle: 设置底纹的斜率。
• density: 底纹的密度。默认值为 NULL。
• col: 是表示每个扇形的颜色，相当于调色板。

> # 数据准备
> info = c(1, 2, 4, 8)
> 
> # 命名
> names = c("Google", "Runoob", "Taobao", "Weibo")
> 
> # 涂色（可选）
> cols = c("#ED1C24","#22B14C","#FFC90E","#3f48CC")
> 
> # 计算百分比
> pieper = paste(round(100*info/sum(info)), "%")
> 
> # 绘图
> pie(info, labels=pieper, col=cols, main='网站分析')
Hit <Return> to see next plot: 
> # 添加颜色样本标注
> legend("topright", names, cex=0.8, fill=cols)

函数图

R中curve()函数可以绘制函数的图像，也可以直接使用plot，代码格式如下：

plot(x, y = 0, to = 1, from = y, xlim = NULL, ylab = NULL, …)

curve(expr, from = NULL, to = NULL, n = 101, add = FALSE,
      type = "l", xname = "x", xlab = xname, ylab = NULL,
      log = NULL, xlim = NULL, …)

• expr：函数表达式
• from 和 to：绘图的起止范围
• n：一个整数值，表示 x 取值的数量
• add：是一个逻辑值，当为 TRUE 时，表示将绘图添加到已存在的绘图中。
• type：绘图的类型，p 为点、l 为直线， o 同时绘制点和线，且线穿过点。
• xname：用于 x 轴变量的名称。
• xlim 和 ylim 表示x轴和y轴的范围。
• xlab，ylab：x 轴和 y 轴的标签名称。

> curve(sin(x), -2 * pi, 2 * pi,main='sin')

> # 生成x轴上的坐标
> x <- seq(-2*pi, 2*pi, length.out = 100)
> 
> # 计算sin函数的值
> y <- sin(x)
> 
> # 绘制图像
> plot(x, y, type = "l", col = "blue", xlab = "x", ylab = "sin(x)", main = "sin function")
Hit <Return> to see next plot: 

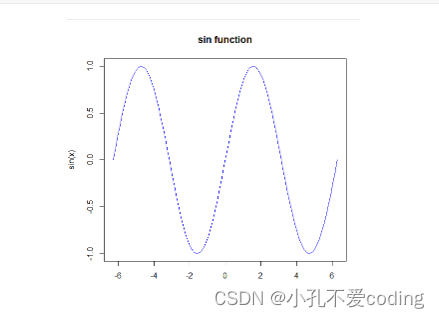
ggplot

> library(ggplot2)
> # 准备数据
> data <- data.frame(x=rnorm(100), y=rnorm(100))
> # 使用ggplot绘制散点图
> ggplot(data, aes(x=x,y=y)) + geom_point()

这段代码首先使用ggplot函数创建了一个空白的绘图对象，并指定输入数据和x,y轴的映射关系；然后通过+符号添加了一个图层，使用geom_point函数绘制散点图

other

1. 使用ag.csv绘制放假和房屋面积的散点图
# 使用plot
> w=read.csv("ag.csv")
> for (i in c(6:10,12)) {
+     w[,i]=factor(w[,i]) # 分类变量因子化
+ }
> plot(sell~lot,data = w)
# 使用ggplot
ggplot(data=w,aes(x=lot,y=sell))+geom_point()
# 加一层loess曲线
> ggplot(data=w,aes(x=lot,y=sell))+geom_point()+geom_smooth(method = loess, se=FALSE)
`geom_smooth()` using formula = 'y ~ x'
##############################################

# 读入数据保存为df
df <- read.csv("kyb.csv")
# 查看数基本信息
summary(df) # 查看基本统计信息
str(df) # 查看数据类型和结构
head(df) # 查看前几行数据
tail(df) # 查看后几行数据
# 保存图像为pdf
pdf("myplot.pdf")
# 绘制图形的代码
dev.off()

#打开一个新的作图窗口
< x11()

# plot函数：它是R中最常用的画图命令，可以绘制大多数常用的点图、线图。

有监督学习概论

机器学习：通过算法从模型集里面选出一个最贴近观察记录的模型，用来表示我们想要的关系结构要刻画“贴近”的程度，需要一个量化标准，我们称之为策略

机器学习是利用计算机算法，通过对大量数据进行训练和学习，自动发现数据之间的规律和模式，并应用这些规律和模式进行预测和决策的过程。

区分是否是有监督学习：是否有目标变量(因变量)；训练数据是否有标签

人工神经网络

神经网络的定义

人工神经网络是一种模拟生物神经系统的结构和行为，进行分布式并行信息处理的算法数学模型。从一组输入数据中进行学习，根据这一新的认知调整模型参数，以发现数据中的模式。

人工神经网络的基本处理单元——人工神经元

神经网络的特征

神经网络的优势：

1. 能较好的模拟人的形象思维

   2. 具有大规模并行协同处理能力
   3. 具有较强的容错能力和联想能力
   4. 具有较强的学习能力
   5. 避免了复杂数学推导
   6. 大规模、自组织、自适应的非线性动力系统

神经网络的不足：

1. 结构复杂，可解释性差

   2. 训练时间长
   3. “黑箱”特性，难以理解网络的具体学习和决策过程

BP神经网络(back-propagation)

前向网络(BP网络)：神经元分层排列(输入层、隐藏层和输出层)。各层之间的神经元全互联，各层内的神经元无互联。每一层只接受来自前一层的输入。

BP算法的具体步骤

1. 从训练例集中取一样例，把输入信息输入到网络中

   2. 由网络分别计算各层节点的输出
   3. 计算网络的实际输出与期望输出的误差
   4. 从输出层反向计算到第一个隐藏层，按照一定原则向减小误差的方向调整网络的各个连接权值-反向传播
   5. 对训练样例集中的每一个样例重复以上步骤，直到对整个训练样例集的误差达到要求时为止

BP网络的优点

1. 全局逼近，泛化能力较好
2. 连接权个数多，较好的容错性
3. 全连接，具有很好的逼近非线性映射能力，可应用于信息处理、图像识别、模型辨识、系统控制等。

BP网络的缺点

1. 参数多，收敛速度慢
2. 局部极值问题
3. 难以确定隐藏层和隐节点的个数

卷积神经网络

卷积神经网络（Convolutional Neural Network，CNN）是一种前馈神经网络，由多层感知机（MLP）演变而来，由于其具有局部区域连接、权值共享、降采样的结构特点，它由若干卷积层和池化层组成，尤其在图像处理方面CNN的表现十分出色。(降低反馈神经网络的复杂性)

CNN基本结构

CNN的基本结构由输入层、卷积层(convolutional layer)、池化层(pooling layer，也成为取样层)、全连接层及输出层构成。卷积层和池化层一般会采取若干个，采取卷积层和池化层交替设置。

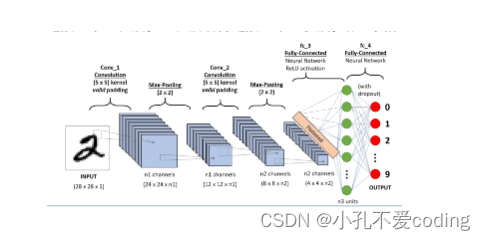
卷积层

在卷积层中，通常包含多个可学习的卷积核，上一层的输出的特征图与卷积核进行卷积操作，即输入项与卷积核之间的点积运算，然后将结果送入激活函数。

问题：

1. 每次卷积会导致图像尺寸变小，如果图像很小，进行多次卷积最后可能只会剩下一个元素

   2. 输入图像的矩阵边缘像素只被计算过一次，而中间像素被卷积计算多次，这就意味着丢失图像边缘信息，需要对图像进行填充。

CNN特点

1. 权值共享
2. 局部连接。区别于全连接

这些特点的作用在于降低了网络模型的复杂度，减少了权值的数目

降采样，池化(Pooling)，池化的好处是降低了特征的维度，即降低了图像的分辨率，整个网络也不容易过拟合

卷积运算

按照kernel的形状移动窗格即可

为什么卷积层会有多个卷积核？/权值共享

1. 卷积核用于检测特征，多个卷积核可以学习到更多的特征，从而提高网络的识别准确性
2. 多个卷积核也可以减少参数的数量，降级过拟合风险

前馈和反馈神经网络的区别

前馈神经网络：

1. 没有循环连接，只有前向连接
2. 数据流只向前传播，不会形成环路，因此适合处理静态数据，如图像和文本等
3. 训练速度快(相对于反馈网络)，但对于复杂的非线性问题不够强大
4. 通常被用来分类、回归和聚类等任务
5. 例如MLP,CNN等

反馈神经网络

1. 可以有循环连接，可以产生内部状态
2. 可以对动态数据进行处理，如时间序列，语音信号等
3. 反馈神经网络具有非常强的非线性建模能力，但训练速度慢
4. 常用于预测，控制和动态系统建模等
5. 例如RNN,HMM等

循环神经网络(recurrent neural network， RNN)

RNN是一种用于处理序列数据的神经网络。相比一般的神经网络来说，能够处理序列变化的数据

循环神经网络的隐藏层的值不仅仅取决于当前这次的输入x，还取决于上一次的隐藏层的值s

LSTM(Long short-term memory, 长短期记忆)

LSTM是一种特殊的RNN，能够解决”长期依赖“的问题

LSTM中的门

LSTM能够给细胞状态增加或者删除信息，是由一种叫作”门“的结构来控制的。

1. 遗忘门(sigmoid层)：决定丢弃哪些信息
2. 输入门(sigmoid层)：决定输入中的哪些值来更新记忆状态
3. 输出门(sigmoid层)：决定输出哪些信息。

支持向量机(support vector machine SVM)

支持向量机根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷，以获得最好的泛化能力。

支持向量机既可用于分类也可用于回归。

支持向量机是一种二分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机学习策略是间隔最大化，最终可转化为一个凸二次规划问题的求解。

SVM在解决小样本、非线性等分类问题中表现出许多特有的优势，可以应用于人脸识别，文本分类，手写数字识别等。

核函数的选择”是SVM算法性能的最大变数

1. 最大间隔：SVM 的目标是找到一个最大间隔超平面，即在样本空间中使得正负样本间距离最大的超平面。

最大间隔超平面在分类时具有更好的鲁棒性和泛化能力，可以有效避免过拟合的问题。这是因为最大间隔超平面距离两个类别的数据点都最远，这就保证了分类的稳定性和准确性。同时，最大间隔超平面也能够最大化分类边界的距离，这在遇到新的数据集时，能够更加容易地进行分类。

2. 支持向量：最大间隔超平面与每个类别最靠近超平面之间的距离由一些样本点决定，这些样本点被称为支持向量。

3. 核函数：如果数据集线性不可分，SVM 采用核函数将数据映射到高维空间中，使得数据集在高维空间中变得线性可分。

SVM的核函数可以用来将数据从原始空间映射到高维空间中，从而使得非线性问题可以在高维空间中被解决

4. 正则化：SVM 通过限制间隔来控制模型的复杂度，从而防止过拟合，常用的方法是 L1 正则化和 L2 正则化。

5. 软间隔：SVM 中还存在软间隔，即允许一定数量的样本点落在超平面错误的一侧，以解决数据集中存在异常值或噪声的情况。

6. 多类分类：SVM 原本是二分类问题，但可以通过多种方法将其扩展到多类分类问题，比如一对多和一对一方法。

组合算法

决策树是组合方法最常用的一类基学习器，组合方法是通过多个学习器(分类或回归模型)来提高预测精度

组合算法主要包括bagging、boosting和随机森林

组合方法：采用有放回的抽样，所产生的数据集合决策树互不相同，从不同的决策树得到的预测也不相同，这些差异结合起来产生更好的预测效果。

自助采样和蒙特卡洛方法都是有放回再抽样

从一个数据集所得到的等可能的有放回再抽样的样本服从原数据集的经验分布

在较大样本时, 经验分布和抽样的频数分布很接近.

弱学习器常指泛化性能略优于随机猜测的学习器

个体学习器间不存在强依赖关系，可并行生成的训练方法，代表算法是bagging和随机森林

个体学习器间存在强依赖关系，必须串行生成的序列化方法，boosting算法

bagging

有放回等可能地重复抽样，对每个样本建立一个决策树，分别预测，等权投票。

1. bagging算法在基预测器不稳定的情况下很有用，而当基预测器稳定时，bagging算法不一定有效
2. bagging算法可以让好的分类器更好，让坏的分类器更坏
3. 增加bootstrap(自助采样)抽样样本量个数并不能提高bagging算法的精度

随机森林

随机森林在bagging的基础上加入了随机特征选择，在每个子数据集上训练基本模型时，只考虑随机选择的一部分特征。

优点：

1. 训练和预测速度块
2. 能够处理很高维度的数据，并且不用做特征选择
3. 对训练数据的容错能力强，当数据集中有大比例的数据缺失时仍可以保证准确率
4. 能够检测到特征之间的相互影响以及重要性程度
5. 不容易出现过拟合
6. 实现简单容易并行化

缺点：

1. 无法控制模型内部运行，不易解释
2. 由于随机特征选择，单颗决策树效果差
3. 对回归问题欠佳，在某些具有特定噪声的数据进行建模时容易出现过拟合

adaboost

adaboost和bagging相似，通过有放回抽样的不同样本建立许多决策树，但是在第一颗树之后，抽样不是等概率的，而是对于前一棵树错判的观测值增加被抽中的概率来为下一颗树抽样。目的是增加那些在前一棵树被错判的观测值的代表性，而增加其判对的机会。每一次都如此抽样，并记录每一颗树的误判率。最后的结果不是简单多数，而是根据各个决策树的误判率来加权投票，准确率高的树权重就大。

模型评价

ROC曲线与AUC

ROC曲线是一种用于评价二元分类模型的可视化工具。ROC曲线的横轴是伪正例率(False Positive Rate,FPR)，纵轴是真正例率(True Positive Rate，TPR)。当分类器分类效果越好时，ROC曲线越向左上凸起；分离效果越差，ROC曲线越向右下凹陷。ROC曲线下面积越大，分类器性能越好，ROC曲线下面面积越小，分类器性能越差。

AUC

1. 当模型预测结果和随机猜测没有区别时，ROC曲线为左下到右上的对角线，AUC=0.5
2. 当模型预测结果好于随机猜测时，ROC曲线为向左上凸起的曲线，0.5<AUC<1
3. 当模型预测结果不如随机猜测时，ROC曲线为右下凹陷的曲线，0<AUC<0.5

通常AUC达到0.8以上，认为模型效果较好。

过拟合

如果用训练集所得到的误判率和用测试集得到的误判率之间的差别很大，则说明该模型有过拟合现象。

交叉验证

为了验证一个模型是否具有普适性，用一部分数据集来训练模型，而用另一部分数据集来测试该模型的预测精度。

k折交叉验证

把数据分成k份，每次交叉验证时，用1份作为测试集，而剩下的k-1份合起来作为训练集，如此可以轮流做k次交叉验证，汇总起来就可以得到模型的交叉验证的精确度。

习题

1. 生成由5个2组成的向量
> rep(2,5)
[1] 2 2 2 2 2
######################################################################################################
######################################################################################################
2. 将'1','a'依次重复3遍
> c = c(1,'a')
> c
[1] "1" "a"
> rep(c,3)
######################################################################################################
######################################################################################################

[1] "1" "a" "1" "a" "1" "a"
3. 生成依次由10个1，20个3和15个2组成的向量
> vec = c(rep(1,10), rep(3,20), rep(2,15))
> vec
 [1] 1 1 1 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
[30] 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

######################################################################################################
######################################################################################################
4. 有监督学习和无监督学习的区别是什么：有无目标变量
######################################################################################################
######################################################################################################
5. 安装pacman这个包【install.packages("pacmnan")】，并载入此包【library(pacman)】，输出这个包的帮助信息【help(package="pacman")】         【注意install和help有引号；library无引号】
【pacman 包是一个整合了基础包 library 相关函数的包，用于更方便地对R包进行管理。】

######################################################################################################
######################################################################################################
6. 查看函数box的帮助信息的语句【help(box)】【?box】
######################################################################################################
######################################################################################################
7. 生成10个0-2范围内符合均匀分布的随机数
> runif(10, min=0, max=2)
 [1] 0.6558414 1.9090073 1.7790786 1.3856068 1.2810136
 [6] 1.9885396 1.3114116 1.4170609 1.0881320 1.1882840
######################################################################################################
######################################################################################################

8. 将工作目录设置为D盘document文件夹(非新增)的R语言语句
setwd("D:/document")
######################################################################################################
######################################################################################################

9. 将工作目录设置为D盘document文件夹(新增)的R语言语句
dir.create("D:/document_new")
setwd("D:/document_new")
######################################################################################################
######################################################################################################
10. 查看image函数的示例
example("image")或demo(image)
######################################################################################################
######################################################################################################

11. 切片操作
a = c("k","j","h","a","c","m")
11.1 提取第三个元素
< a[3]  # R语言下标从1开始
11.2 提取奇数位置的元素
a[c(1,3,5)]或a[seq(1,length(a),2)]，从第一个元素开始步长为2
11.3 提取位置2-6的元素
a[2:6]
######################################################################################################
######################################################################################################

12. 构造向量a为[2:6]
a = c(2:6)
######################################################################################################
######################################################################################################

13. 将a的第五个元素修改为-6
a[5] = -6
######################################################################################################
######################################################################################################

14. 排序向量a，降序
sort(a, decreasing=T)
######################################################################################################
######################################################################################################

15. 反转向量a
rev(a)
######################################################################################################
######################################################################################################

16. 填空题
首先，创建了一个名为x的向量对象，包含5个服从标准正态分布的
随机数【x <- rnorm(5)】
采用which函数确定最大值位置【max_idx <- which(x == max(x))】
采用which函数确定最小值的位置【min_idx <- which(x == min(x))】
采用which函数确定大于1的位置【greater_than_1_idx <- which(x > 1)】
> x <- rnorm(5)
> x
[1] -0.5558411  1.7869131  0.4978505 -1.9666172  0.7013559
> max_idx <- which(x == max(x))
> max_idx
[1] 2
> min_idx <- which(x == min(x))
> min_idx
[1] 4
> greater_than_1_idx <- which(x > 1)
> greater_than_1_idx
[1] 2
######################################################################################################
######################################################################################################
17. 使用循环语句解决下述问题：本金10000元存入银行，年利率是百分之三，每过1年，将本金和利息相加作为新的本金。计算10年之后，获得收益共是多少？ 
> principal <- 10000
> rate <- 0.03
> # 计算十年后的本金和利息
> for(i in 1:10){
+     principal <- principal*(1+rate)
+ }
> # 输出结果
> cat("十年后的收益：", round(principal-10000,2))
十年后的收益： 3439.16
######################################################################################################
######################################################################################################
18. 加载vcd中的Arthritis数据验证`改善情况`和`性别`的独立性
> # 调用vcd包
> head(Arthritis)
  ID Treatment  Sex Age Improved
1 57   Treated Male  27     Some
2 46   Treated Male  29     None
3 77   Treated Male  30     None
4 17   Treated Male  32   Marked
5 36   Treated Male  46   Marked
6 23   Treated Male  58   Marked
> # 选取改善情况和性别生成列联表
> mytable <- xtabs(~Improved+Sex, data=Arthritis)
> mytable
        Sex
Improved Female Male
  None       25   17
  Some       12    2
  Marked     22    6
> # 进行卡方检验
> chisq.test(mytable)

	Pearson's Chi-squared test

data:  mytable
X-squared = 4.8407, df = 2, p-value = 0.08889

[从卡方检验结果可以看出，卡方值为4.8407，自由度为2，P值为0.08889，因此不能拒绝原假设。也就是说，在显著性水平为0.05的情况下，没有足够的证据表明性别和治疗改善情况之间存在显著的关系。]

19. 以数据集ag.csv中sell和lot两个变量绘图，类型为散点图，点的形式为`+`

> # 读取数据
> ag <- read.csv(("E:/1作业/大三下/数据分析语言/ag.csv"))
> head(ag)
   sell  lot bdms fb sty drv rec ffin ghw ca gar reg
1 42000 5850    3  1   2   1   0    1   0  0   1   0
2 38500 4000    2  1   1   1   0    0   0  0   0   0
3 49500 3060    3  1   1   1   0    0   0  0   0   0
4 60500 6650    3  1   2   1   1    0   0  0   0   0
5 61000 6360    2  1   1   1   0    0   0  0   0   0
6 66000 4160    3  1   1   1   1    1   0  1   0   0
> # 绘制散点图
> plot(ag$sell, ag$lot, pch='+', xlab='Sell', ylab='Lot')

######################################################################################################
######################################################################################################
20. Bagging算法中各个学习器之间为并行训练方式
	Adaboost算法中各个学习器之间为串行训练方式
###############################################################
21. 在[-1,2]上画y=e^(2x) + sin(3x^2)的图像
> x <- -1:2
> y = exp(2*x) + sin(3*x^2)
> plot(x,y,type = 'l')
############################################3
22. 绘制线图Y = 2sin(x),x∈[0,2Π]

> x <- seq(0,2*pi,0.01)  # 生成了一个从0到2π的数列，间隔为0.01
> y = 2*sin(x)
> plot(x,y,type = 'l')

solution2：
x <- seq(0, 2 * pi, length.out = 100) # 生成0到2π的100个等间距数列作为x坐标值
y <- 2 * sin(x) # 计算对应的y坐标值
plot(x, y, type = "l", col = "blue", lwd = 2, xlab = "x", ylab = "y", main = "y = 2sin(x)") # 绘制曲线
################################################
23. 首先绘制图Y=2sin(x),x∈[0,2Π]，并将该绘图改为点图，并加标题“画图练习”
子标题“练习”，横坐标命名为x轴，纵坐标命名为y轴
> x <- seq(0,2*pi, length.out = 100)
> y = 2*sin(x)
> plot(x,y,main  = "画图练习",sub = "练习",xlab = "x", ylab = "y轴")
#################################################################3

e)

Pearson's Chi-squared test

data: mytable
X-squared = 4.8407, df = 2, p-value = 0.08889

[从卡方检验结果可以看出，卡方值为4.8407，自由度为2，P值为0.08889，因此不能拒绝原假设。也就是说，在显著性水平为0.05的情况下，没有足够的证据表明性别和治疗改善情况之间存在显著的关系。]

```R
19. 以数据集ag.csv中sell和lot两个变量绘图，类型为散点图，点的形式为`+`

> # 读取数据
> ag <- read.csv(("E:/1作业/大三下/数据分析语言/ag.csv"))
> head(ag)
   sell  lot bdms fb sty drv rec ffin ghw ca gar reg
1 42000 5850    3  1   2   1   0    1   0  0   1   0
2 38500 4000    2  1   1   1   0    0   0  0   0   0
3 49500 3060    3  1   1   1   0    0   0  0   0   0
4 60500 6650    3  1   2   1   1    0   0  0   0   0
5 61000 6360    2  1   1   1   0    0   0  0   0   0
6 66000 4160    3  1   1   1   1    1   0  1   0   0
> # 绘制散点图
> plot(ag$sell, ag$lot, pch='+', xlab='Sell', ylab='Lot')

######################################################################################################
######################################################################################################
20. Bagging算法中各个学习器之间为并行训练方式
	Adaboost算法中各个学习器之间为串行训练方式
###############################################################
21. 在[-1,2]上画y=e^(2x) + sin(3x^2)的图像
> x <- -1:2
> y = exp(2*x) + sin(3*x^2)
> plot(x,y,type = 'l')
############################################3
22. 绘制线图Y = 2sin(x),x∈[0,2Π]

> x <- seq(0,2*pi,0.01)  # 生成了一个从0到2π的数列，间隔为0.01
> y = 2*sin(x)
> plot(x,y,type = 'l')

solution2：
x <- seq(0, 2 * pi, length.out = 100) # 生成0到2π的100个等间距数列作为x坐标值
y <- 2 * sin(x) # 计算对应的y坐标值
plot(x, y, type = "l", col = "blue", lwd = 2, xlab = "x", ylab = "y", main = "y = 2sin(x)") # 绘制曲线
################################################
23. 首先绘制图Y=2sin(x),x∈[0,2Π]，并将该绘图改为点图，并加标题“画图练习”
子标题“练习”，横坐标命名为x轴，纵坐标命名为y轴
> x <- seq(0,2*pi, length.out = 100)
> y = 2*sin(x)
> plot(x,y,main  = "画图练习",sub = "练习",xlab = "x", ylab = "y轴")
#################################################################3