一、高斯消去法
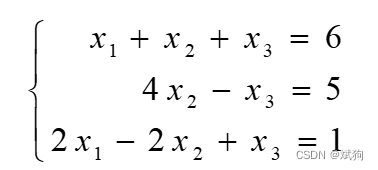
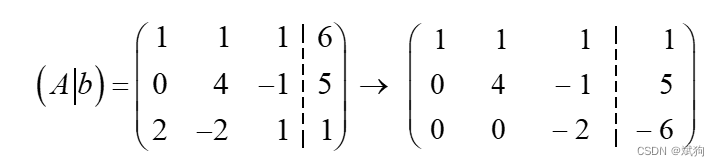
比如对与上面的这个方程组,用消去法解方程组的基本思想是用逐次消
去未知数的方法把原方程组 Ax = b 化为与其等价的三角形方程组,而求解三角形方程组可用回代的方法.。
大体过程主要分为消去与回代

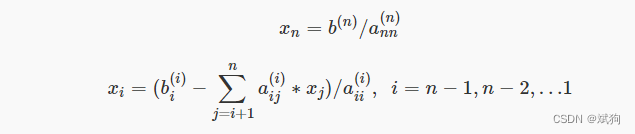
function solution =gaosi(A,b)
n = length(b);
for k=1:n-1
for i=k+1:n
mik=A(i,k)/A(k,k);%消元因子
for j=k+1:n
A(i,j)=A(i,j)-mik*A(k,j);
end
b(i)=b(i)-mik*b(k);
end
end
solution(n)=b(n)/A(n,n);
for i=n-1:-1:1
for j=i+1:n
solution(i)=solution(i)+A(i,j)*solution(j);
end
solution(i)=(b(i)-solution(i))/A(i,i);
end
end
python
import numpy as np
def gaosi(A,b):
[n, m] = b.shape
solution = np.zeros((n, m))
for k in range(0,n-1):
for i in range(k+1,n):
mik=A[i,k]/A[k,k]
for j in range(k+1,n):
A[i,j]=A[i,j]-mik*A[k,j]
b[i]=b[i]-mik*b[k]
solution[n-1]=b[n-1]/A[n-1,n-1]
for i in range(n-2,-1,-1):
for j in range(i+1,n):
solution[i]=solution[i]+A[i,j]*solution[j]
solution[i]=(b[i]-solution[i])/A[i,i]
return solution
A = np.array([[10,-7,0,1],[-3,2.099999,6,2],[5,-1,5,-1],[2,1,0,2]])
b = np.array([[8],[5.900001],[5],[1]])
print(gaosi(A,b))
二、高斯列主元消去法
基于高斯消去法的改进,当列主元出现数值较小时,在消去的过程列主元会作为分母,导致误差的出现。基于此,列主元消去是将每一次的主元通过行互换,用绝对值最大的列主元进行消去
function solution = liezhuyuan(A,b)
n = length(b);
for k=1:n-1
[value position]=max(abs(A(k:n,k))); %主元所在位置和主元的值
if position~=1 %若a(k,k)不是绝对值最大的,换位置
a_k_position=A(k,k:n);
b_k_position=b(k);
A(k,k:n)=A(position+k-1,k:n);
A(position+k-1,k:n)=a_k_position;
b(k)=b(position+k-1);
b(position+k-1)=b_k_position;
end
% 后面消元
for i=k+1:n
mik=A(i,k)/A(k,k);
for j=k+1:n
A(i,j)=A(i,j)-mik*A(k,j);
end
b(i)=b(i)-mik*b(k);
end
end
solution(n)=b(n)/A(n,n);
for i=n-1:-1:1
for j=i+1:n
solution(i)=solution(i)+A(i,j)*solution(j);
end
solution(i)=(b(i)-solution(i))/A(i,i);
end
end
三、Lu分解

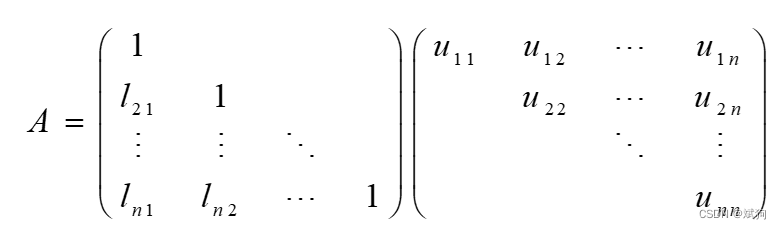
function [x,y,L,U] = LUfenjie(A,b)
% 输入
% A = [2 1 5;4 1 12;-2 -4 5]
% b=[11;27;12]
% 输出
% x =
% 1 -1 2
% y =
%
% 11 5 8
% 注意L分解出的结果只有下三角,主对角线为1
% L =
%
% 0 0
% 2 0
% -1 3
% U =
% 2 1 5
% 0 -1 2
% 0 0 4
n = length(b);
U(1,:)=A(1,:);
L(2:n,1)=A(2:n,1)/U(1,1);
for k=2:n
for j=k:n
U(k,j)=A(k,j)-L(k,1:k-1)*U(1:k-1,j);
end
for i=k+1:n
L(i,k)=(A(i,k)-L(i,1:k-1)*U(1:k-1,k))/U(k,k);
end
end
y(1)=b(1);
for i=2:n
y(i)=b(i)-L(i,1:i-1)*y(1:i-1)';
end
x(n)=y(n)/U(n,n);
for i=n-1:-1:1
x(i)=(y(i)-U(i,i+1:n)*x(i+1:n)')/U(i,i);
end
四、追赶法
追赶法只有当矩阵为三对角矩阵时才能使用(形如这样的)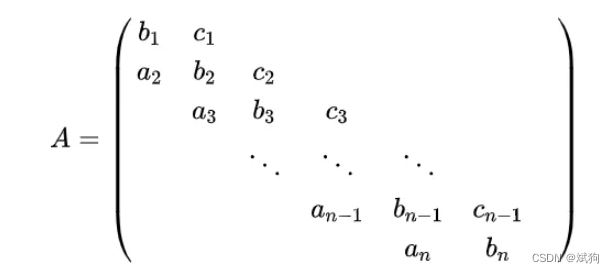
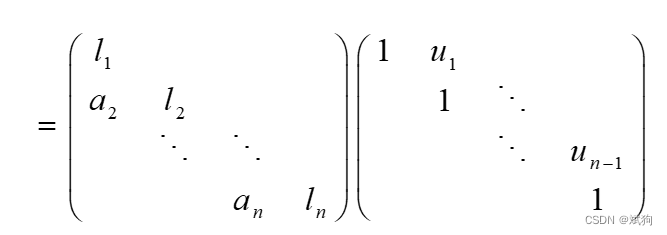
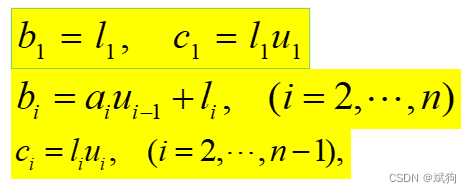
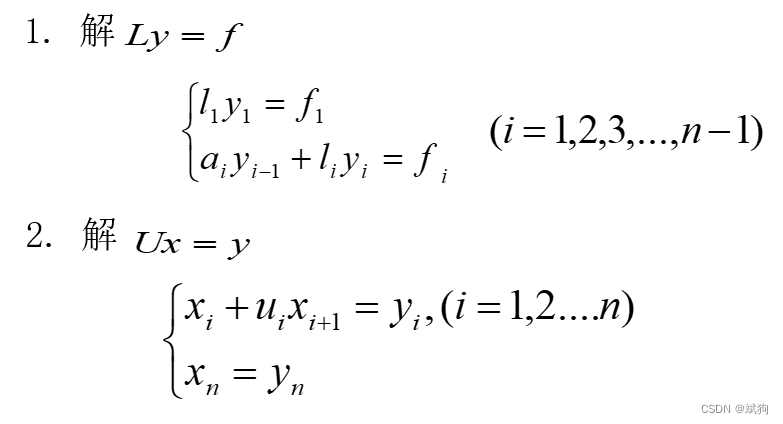
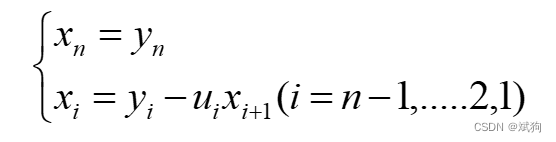
矩阵为三对角矩阵时 ,用a,b,c 存储。 a为下对角线元素,b为对角线,c为上对角线。
function x =zhuigan(a,b,c,f)
%a下三角列(前面加0),b为主对角线,c为上三角,f为右端向量
%a,b,c为行向量,f为列向量
%如输入a = [0 1 1 1]
% b=[4 4 4 4]
% c = [2 2 2]
% f=[1;2;3;4]
% zuigan(a,b,c,f)
%输出
% ans =
% 0.0488 0.4024 0.1707 0.9573
%rats(ans)=
% 2/41 33/82 7/41 157/164
n=length(f);
l(1)=b(1);
for i=1:n-1
u(i)=c(i)/l(i);
l(i+1)=b(i+1)-a(i+1)*u(i);
end
y(1)=f(1)/l(1);
for i=2:n
y(i)=(f(i)-a(i)*y(i-1))/l(i);
end
x(n)=y(n);
for i=n-1:-1:1
x(i)=y(i)-u(i)*x(i+1);
end
end





















 1231
1231











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








