开个文章补一下白版推导吧,现在回过头来看这些都还是挺有用的,不把数学底层逻辑理清总有一种学了又好像没学的感觉。

1. 绪论
1.1. 机器学习的两大流派——频率派和贝叶斯派
1.1.1. 频率派:统计机器学习
- 建模方法:概率派将模型参数
视为一个常量,样本
是一个随机变量,使用极大似然估计(Maximum Likelihood Estimate,MLE)方法建模求得
的解,即
1.1.2. 贝叶斯派:概率图模型
- 建模方法:认为模型参数
是一个随机变量,其遵从的分布
被称为先验分布(没见到样本就有的概率分布),根据贝叶斯公式计算后验概率
,则寻找最大后验估计(Maximum a Posteriori estimation,MAP),即
,和MLP相比仅多了一项 ;
- 求解后验概率时,分母的积分计算是复杂的,因此通常采用蒙特卡洛采样法来代替;
- 当先验分布遵从高斯分布时,
,为常数,因此
,相当于在MLP优化函数中增加一项L2正则化
- 贝叶斯预测:已有数据为
,预测新数据
时,需要计算新的后验概率
1.2. 数学基础
1.2.1. 矩阵迹的性质
1.2.2. 克罗内克积(Kronecker Product)
以的元素保持相对位置分别乘以
1.2.3. 奇异值分解(Singular Value Decomposition,SVD)
- 类似于特征值分解,奇异值分解也是将矩阵分解为需要的矩阵,而特征值分解只能处理方针,奇异值分解则是针对非方针提出;
- 定义:对于一个矩阵
,存在两个酉矩阵
和
,
,
,使得
,其中
主对角线上元素为奇异值,其他位置元素为0;
- 求解:对
进行特征值分解得到的特征向量经过正交单位化后拼接为
(假设
成立,则
,下面的证明同理),再对
进行特征值分解得到特征向量经正交单位化后拼接为
,而
或
前
个特征值的根号即为奇异值,也就是
主对角线元素;
- 性质:
- 对于
的第
列
(
)及
对应列
,有
,或
,其中
为
对应位置奇异值,而当
或
时,
;
- 奇异值通常从大到小排列,但递减得特别快,很多情况下前10%甚至1%的奇异值之和就占了全部奇异值之和的99%以上,因此有时可以用一部分来描述奇异值分解:
,其中
比
小得多,这个性质也是PCA的重要基础;
- 对于
1.2.4. 矩阵求导
因此
1.2.5. Jensen不等式
- 对任意凸函数,其上两点
和
,有
;
- 推广对任意
,有
;
- 推广对任意随机变量
,有
;
2. 高斯分布
2.1. 高维高斯分布的理解
2.1.1. 马氏距离
- 对于两个向量
和
,其马氏距离为
,
为每个特征对应距离的权重,是一个正定对称矩阵,当
时,马氏距离退化为欧氏距离(p维空间两个坐标点的空间距离)
;
2.1.2. 推导
- 高斯分布的概率密度函数为:
令,因为
是一个正定对称矩阵,因此可以对其进行矩阵分解,存在正交矩阵
和对角阵
,使得
因此可得
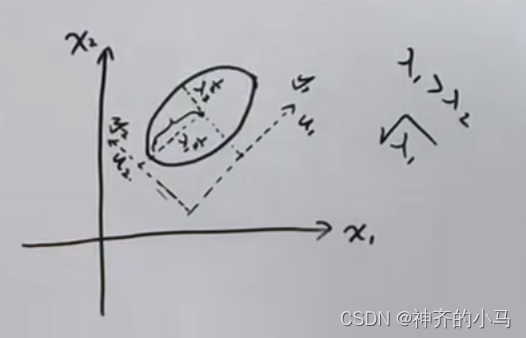
最终得到的结果在等于定值的情况下(例如)为一个高维空间的椭球体,其中经过的投影
即为将该球体球心移至坐标原心,再对每个
坐标轴分别进行投影的过程(下图中长短轴分别为
和
);
2.2. 极大似然估计
2.2.1. 问题定义:
- 对于一组数据
,其未知参数为
,对其进行极大似然估计;
2.2.2. 过程推导
- 似然函数
将概率密度函数带入得:
对求导,并令其为0,则有:
再对求导:
又根据,可得:
令其为0,可得:
- 对高斯分布进行极大似然估计是一种有偏估计,均值无偏而方差有偏,估计得到的
,
,而真正的无偏估计为
;
2.3. 高斯分布的局限性
- 协方差矩阵
尺寸为
,虽然其为实对称,但参数量依然有
个,对于机器学习类问题,特征维度往往很大,需要学习的参数量也就很大,常见的解决方法有:
- 将
矩阵近似为对角阵;
- 利用
的线性变换将
矩阵变为单位阵(或单位阵的k倍);
- 将
- 复杂性不够,很多数据的分布难以用一个分布拟合;
2.4. 高维高斯分布的边缘概率分布
2.4.1. 问题定义
- 对于一组数据
,可将其分为两组
,其中
为
维向量,
为
维向量,
,因此则可以将其他参数划分为
,
;
- 此时概率密度函数
可以认为是联合概率分布
;
- 需要求的是边缘概率密度
;
2.4.2. 定理基础
- 高斯分布的线性定理:若
,则对于
,有
;
2.4.3. 过程推导
- 首先对于
,可以写成矩阵形式:
;
- 则可以令
,可得
;
- 因此
,同理可得
;
2.5. 高维高斯分布的条件概率分布
2.5.1. 问题定义
- 同2.4.,
,
,
;
- 需要求的是条件概率密度
;
2.5.2. 过程推导
- 根据schur complementary矩阵*,可设定一个中间量
;
- 对其求期望和方差可得:
,
;
- 记
,
,则
;
- 因此
,则
,
,则
,同理可得
2.6. 线性高斯模型对称求解
2.6.1. 问题定义
- 已知
,求
;
,
和
相互独立;
2.6.2. 过程推导
- 首先求
,
,
,可得
;
- 再求解
,直接求解比较复杂,因此我们先求
和
的联合概率分布,再通过2.5的结论套用即可得到结果;
- 易知
,其中
是需要求解的;
- 令
,即可套用2.5的计算
的结论计算
;
3. 线性回归
3.1. 最小二乘法
3.1.1. 问题定义
,
,
;
- 对于增广矩阵
,需要找到一个参数矩阵
,使得
;
3.1.2. 求出解析解
;
- 将这个损失函数对参数矩阵求导可得:
;
- 令其为0,可得
,其中
被称为
的伪逆;
3.2. 概率角度
3.2.1. 问题定义
- 同样是
,
,增广矩阵
,参数矩阵
,
;
- 可以知道,
和
有着一定的线性关系,但真实数据存在随机误差,因此可以定义随机误差
,使得
,则可得
;
3.2.2. 求出解析解
- 使用最大似然估计法求解参数,由
,可得似然函数
,因此优化目标变成了
,与最小二乘法相同;
3.3. 正则化
3.3.1. 为什么要正则化
- 从前面的推论可以知道参数矩阵的解析解
,一般来说
,但特殊情况样本量较小时,可能导致
不可逆,无法求出解析解;
- 从拟合情况看,如果不能满足
,维数较高而样本不足,则容易导致过拟合问题,对于过拟合情况可以用三种方法:
- 采集更多数据;
- 特征选择/特征提取(PCA)
- 正则化
3.3.2. 范数
- 通俗来讲,一个向量的
范数可以定义为
;
- L1范数:Lasso,即为向量各元素的绝对值之和;
- L2范数:Ridge,岭回归,
;
3.3.3. L2正则化
- 正则化的框架:
,即在原有损失函数上加上一个正则化惩罚;
- 对于L2正则化,则对应的优化函数为
,这个优化函数也被称为岭回归;
- 对其进行化简和求导(同3.1.2.)可以得到新的解析解
,解决了
不可逆的问题
3.3.4. 从贝叶斯角度理解线性回归和L2正则化
- 从贝叶斯派的角度求解线性回归问题,则是已知
和
的分布
和
,对于参数矩阵假设一个先验分布
,采用最大后验估计法求解
;
- 假设参数矩阵服从正态分布,即
,则根据贝叶斯公式:
,因为
已知,所以
;
- 根据3.2.1.可知
,因为
已知,所以也可以视为
,因此
;
- 当
(即方差各向同性)时,
,因此有
此时的优化函数和L2正则化是相同的,只是将 替换为了
;
- 使用全量数据求解参数矩阵
(求解线性回归问题):
,其中Quadratic term表示变量的二次项,Linear term表示变量的一次项;
- 根据高斯分布标准形式:
,根据二次项对应系数矩阵可以求得方差矩阵
,进而根据一次项对应系数矩阵可以求得均值向量
;
- 因此将上面两个式子对应联立求解,可得:
;
;
,当
时,取均值结果与3.3.3. L2正则化的解析解形式相同,只是将
替换为了
;
3.4. 线性回归的特性

4. 线性分类
4.1. 线性分类的典型模型
- 硬分类:输出结果只有0或1这种离散结果;
- 线性判别分析 Fisher
- 感知机
- 软分类:会输出0-1之间的值作为各个类别的概率;
- 概率生成模型:高斯判别分析GDA、朴素贝叶斯,主要建模的是
- 概率判别模型:逻辑回归,主要建模的是
- 概率生成模型:高斯判别分析GDA、朴素贝叶斯,主要建模的是
4.2. 感知机
4.2.1. 基本模型
- 模型:
;
- 思想:错误驱动,先随机初始化一个
,研究错误分类的样本来调整
;
- 策略:使用损失函数
,其中
表示错分类的样本;
4.3. 线性判别分析 Fisher
4.3.1. 问题定义
- 对于一个二分类问题,将样本分为
,
,这两组的样本数分别为
和
,
;
- 寻找一个投影超平面
,使所有样本点在这个平面的投影可以做到类内间距小,类间间距大;
4.3.2. 过程推导
- 样本
在超平面
上的投影可以表示为
,
;
- 对投影求方差
,
,
;
,
;
- 类内间距分别为
和
,类间间距为
;
- 为了尽可能类内间距小,类间间距大,将目标函数定义为
,则
;
- 对目标函数进行化简:
;
;
- 同理可得
;
- 所以目标函数化为
;
- 定义类内方差
,类间方差
,因此目标函数被表示为
,对其求导得
,令其为0可得
因为是一个单位向量,所以我们只关心其方向而不关心其长度,所以最终得到
;
4.4. 逻辑回归
4.4.1. 基本思想
- 在线性回归中引入非线性激活函数,使其可以将回归结果映射为概率值,作为类别的概率;
- 将这个模型看做一个条件概率分布的建模,输入
,通过
,输出
的离散取值;
4.4.2. Sigmoid 激活函数
- 基本公式:
;
- 特殊取值:
时,
;
时,
;
时,
;
- 函数图像:

4.4.3. 模型推导
- 根据条件概率建模的思想:
- 因此将整个模型写作
,当
时,
,当
时,
;
- 用极大似然估计法求解模型:
- 求梯度得
4.5. 高斯判别分析
4.5.1. 概率判别式模型与概率生成式模型的区别
- 概率判别式模型主要计算条件概率密度
,取令该概率最大的
为分类结果;
- 概率生成式模型并不需要计算具体的
值,而是直接思考
和
的结果谁更大,根据贝叶斯公式
,将目标函数变为
,其中
,
,可以合并为
;
4.5.2. 高斯概率假设
- 在高斯判别模型中,假设条件分布
是遵从高斯概率分布的,即:
;
- 使用对数似然求解目标函数,可得
4.5.3. 求解模型
- 先求解参数
,先求偏导
,令其为0,求得
,也就是样本中各个标签出现的频率即为最优概率值;
- 再求解参数
,由于其他和
无关的部分求偏导后都得0,所以从目标函数中单独取出和
相关的部分,即
,即
,其中
表示
,因此求解方法等同于高维高斯分布的极大似然估计(2.2.2.),结果为
,同理
;
- 最后求
,同样取出目标函数中和
相关的部分,得:
,对其求偏导得
,令其为0得
,其中
,
,分别为两个类内样本方差;
4.6. 朴素贝叶斯 (Naive Bayes Classifier)
4.6.1. 基本思想
- 所有朴素贝叶斯家族的算法都是基于朴素贝叶斯假设,又叫条件随机场假设,即假设各个特征之间相互独立;
- 朴素贝叶斯模型是最简单的概率图模型;
- 模型方法和高斯判别分析较为接近,这里不做重复;
5. 降维
5.1. 降维的意义
5.1.1. 过拟合问题
- 通常模型通过训练集数据进行训练,若其测试集的效果明显低于训练集,这是一种不理想的效果,称为过拟合;
- 过拟合常采用三种方法应对:
- 采集更多数据,提高模型泛化能力;
- 正则化,抑制模型拟合能力;
- 降维,提取数据中的有效信息;
- 直接降维:特征选择
- 线性降维:PCA
- 非线性降维:流形
5.1.2. 维度灾难
- 从几何角度,若一组数据的特征维度是2,假设两个特征的值都是有上界的,则其构成的样本空间近似一个正方(长)形,数据在这个样本空间中分布;
- 现在要对这组数据进行分类任务,模型映射到样本空间中变成了一条分隔线,将两个类别的样本分隔到了线的两边;
- 为了便于从几何角度直观理解维数灾难,我们假设现在的模型分割线是一个圆,则这个分类模型的示意图如下:

- 将两个特征归一化,样本空间变为了一个边长为1的正方形,面积为1,模型变成了一个半径小于等于
的圆,其包含区域面积为
,占总空间比例小于
;
- 而当模型维度变高时,例如维度为3,此时归一化的样本空间变成了一个三维立方体,体积为1,模型变成了一个三维球面,其包含区域体积为
,占总空间比例小于
;
- 当维度继续升高时,模型表示的这个高维超球面包含区域所占总样本空间的超立方体比例将会越来越小,当维度非常大(趋于无穷)时,超球面包含区域将接近0,;
- 分类边界是一个圆/球面,这是模型内部算法所决定的,而无论这个圆/球面的半径有多大,维度的升高都会导致分类边界仅仅只是样本空间的一个小点,这样的小点也必然无法有好的性能;
- 现在将分类边界也泛化为任意几何体,模型越复杂,通常这个几何体越复杂,但当模型算法确定后,必然存在某个适宜维度使得该几何体可以在样本空间中很好地完成分类任务,而当维度远远大于该适宜维度时,模型都会不再适用;
5.2. 预备统计知识
- 现有数据
- 均值为
,其中
是一个全一列向量;
- 样本方差为
,并经过如下推导:
- 令
称为中心矩阵,则有
,易知
,因此逆推可得
,因此对于任意数据
,
即为对其进行中心化(每个样本减去均值);
,因此可进一步化简
;
5.3. 主成分分析(Principal Component Analysis,PCA)
5.3.1. 核心思想
- 一个中心:原始特征空间的重构(特征之间从相关到无关),即找到一组线性无关的基,可以将原始特征空间的信息尽可能保留地投影到新空间,新空间特征维数低于原空间,这些基被称为主成分;
- 两个基本点:
- 最大投影方差;
- 最小重构距离;
5.3.2. 从最大投影方差看PCA
- 设一个投影方向为
(单位向量),则某个样本
在
方向的投影值为
,因此可得,只需找到
个基(相互线性无关)
,
,则将样本
投影到新特征空间的坐标为
,因此特征变换可以记作
,通过这个线性映射即可完成降维;
- 单看一个投影方向
,其投影结果为
,投影均值为
,投影方差为
- 为了最大化投影方差,将寻找
的问题定义为一个条件优化问题,即
,
,利用拉格朗日算子法得
,求导得
,令其为0可得
,因此
是原样本方差
的特征向量时,投影方差可以被最大化;
- 因此可以求出投影方差
,也就是
对应的特征值即为投影方差,因此PCA就是对原样本方差矩阵
求特征值和特征向量,由于实对称矩阵必可相似对角化,所以必然可以找到
个线性无关的特征向量,将其按照特征值大小排序,取前
个特征值最大的特征向量作为投影方向,每个样本通过这
个投影方向算得新的坐标值即为新的特征,构成了新的
维特征空间,实现了降维;
5.3.3. 从最小重构距离看PCA
- 先看看最小化投影距离:从几何角度,设某个样本
和投影方向
之间的夹角为
,则投影值
,而投影距离为
,因为不同投影方向的坐标值大小不同,因此为了将不同投影方向的情况进行公平对比,可以进行零均值化,此时投影距离的平方为
,而优化目标为
同样约束为,与最大投影方差方法完全一致;
- 从重构角度,一个向量视为该向量空间内基向量的线性组合,例如
,但在另一个向量空间中由不同的基向量会得到不同的坐标表示,例如
,因此在上文的投影中,通过找到
个投影方向可以将样本
投影到新的
维向量空间,坐标为
,因此可以用新空间的坐标和基向量将
表示为
,当
即降维时,基向量信息不完整,即
,无法完全重构,当
时可以完全重构;(其实上文中
,其中
由实对称矩阵
的单位特征向量组成,所以当
时有
,因此
可推成立);
- 因此也可以理解为,当
是按照特征值排序的前
个
时,可以表示为
,同理
,
;
- 因为降维任务会导致
,因此在给定
的情况下,PCA的优化目标也可以理解为最小化重构代价,即
- 因为不同投影方向的坐标值大小不同,因此为了将不同投影方向的情况进行公平对比,可以进行零均值化,即
- 因此从最大化投影方差角度,PCA是在选择
个特征值最大的特征向量,从最小化重构距离的角度,PCA是在选择
个特征值最小的特征向量,将其舍弃,两个问题的等价的;
5.3.4. 从SVD角度看PCA
- 从5.2.中可知,
,若将
作奇异值分解,即
,则
,因此对
进行特征值分解可以得到投影方向
,
也可以是
进行奇异值分解得到的结果,而由奇异值分解的性质(1.2.3.)可知,最大的一小部分奇异值之和就占了所有奇异值之和的99%,因此取前几个奇异值最大的投影方向可以最大程度保留原数据的信息,也就是
;
- 又由奇异值分解的第一个性质(1.2.3.)可得,
,其中
即为所有样本从原始特征空间经方向
投影的坐标值(等同于
,左乘中心矩阵
便得到相同结果),所以奇异值分解的矩阵
其实是坐标矩阵,因此可以再令
,经过特征值分解可以得到坐标矩阵
,这个过程被称为主坐标分析(Principal Coordinate Analysis,PCoA);
6. 支持向量机(Support Vector Machine,SVM)
6.1. 相关概念
6.1.1. 分类
- 硬间隔(Hard-margin)SVM,又叫最大间隔分类SVM;
- 软间隔(Soft-margin)SVM;
- 核(Kernel)SVM;
6.2. 硬间隔SVM
6.2.1. 问题定义:
- 之前的分类算法中,模型致力于寻找一个超平面,可以将训练集中的两类样本分开,但这个超平面理论上存在无数个,它们在训练集上的分类效果可能是相同的,但模型的鲁棒性是不同的,为了寻找最鲁邦的模型,SVM便想要寻找一个所有样本总间隔最大的超平面;
- 首先定义间隔:假设通过一个超平面
,可以完美拟合训练集所有样本,即对任意样本
,都有
,则所有样本中最小的间隔为
;
- 因此硬间隔SVM的优化目标即为最大化这个间隔,使得分类边界具有最高的鲁棒性,即
;
6.2.2. 问题化简:
- 因为
,所以可以写作
,因此优化目标可以写作
;
- 又因为对超平面
,我们只关心其方向,对
无要求,因此对
我们只关心正负,无所谓值的大小,因此对
我们只关心是否大于0,无所谓值的大小,因此为了简化优化目标,可以令
,则优化目标变为
,变为一个凸优化问题;
6.2.3. 问题求解:
- 优化问题首先考虑使用拉格朗日乘数法:
,将带约束的原问题变为无约束优化问题:
;
- 若原问题的约束
不满足,即
,则
,反之若都满足,则
,因此优化目标其实是
,因此这个优化目标函数为了取到
,会调整
使得
对所有
都满足,由此原问题的约束成立;
- 而此时
,因此对任意
,有
,则
或
,由于绝大多数情况,只有两个点离超平面最近(存在更多点距离超平面也是0的理论可能,但实际数据中几乎不存在),即
,其他情况都是
(但这里不能直接带入
,因为这个是目标函数为了达到优化而隐含的约束,如果直接带入则变成了优化之间的已知约束,问题会变得无法求解);

- 这两个最近的样本我们称其为
(
)和
(
),这两个向量被称为支持向量;
- 变为对偶问题:
- 弱对偶关系:
(宁做凤尾,不做鸡头),当中间取等号时变为强对偶关系,而线性约束的二次优化问题天然满足强对偶性(此处不做数学证明);
- 因此这里可以将优化目标变为
;
- 弱对偶关系:
- 求偏导得到结果:
;
;
- 则
;
- 因为对
的优化必须使
和
满足:只有两个点
和
离超平面最近,即
,其他情况都是
,将这个条件带入
可得:
;
- 带入目标函数得
,对其求偏导
,带入得
,因此
,找到两个类中,间距最小的两个样本,计算其欧氏距离可以算得
;
- 再带入
,
即可得到分类边界;
6.3. 软间隔SVM
6.3.1. 引入软间隔的思想
- 硬间隔SVM假设所有样本都可以被完美分类,但实际情况很难做到,因此需要允许一些错误,但又要尽可能控制错误,便有了软间隔SVM的思想;
- 相比于硬间隔,软间隔SVM取消了约束
,而是采用一个损失函数来代替,即设定一组参数
,目标函数变为
;
- 通过这个目标函数,原本间隔外的点(
)的参数
会被优化到0,而间隔内的点无论是否可以被分类正确,都可以尽可能使其向两边分散;
是一个乘法因子,可以作为模型超参数,其作用有点像正则化,
的值越大,
被惩罚得越厉害,间隔小的点越少;
6.3.2. 软间隔SVM的求解
- 前面的部分和硬间隔相同,化为无约束目标函数和对偶优化问题,分别对
和
求偏导后,最终目标函数化简如下:
,
;
- 同样先求得
后(这里需要用到SMO迭代求解算法,过于复杂,后补),即可得到超平面;
7. 核方法
7.1. 背景
- 对于严格线性可分问题,感知机、SVM等算法都可以提供很好的解决方案,但对于非线性分类问题,需要一个非线性转换来将其变为线性问题;
- 高维空间往往比低维空间更容易线性可分,因此可以通过一些非线性变换将已知维度计算出新的维度,便有可能将非线性问题变为线性问题;
- 然而在实际问题中,可以将非线性问题转化为线性问题的变换函数
可能是非常复杂的,而根据概率派思想,将一个问题最终看做一个优化问题,则往往需要计算内积,如
,这会给优化带来非常可怕的复杂度;
- 事实上,我们所关心的是最终的内积的值,而不需要
的结果,因此如果有一个函数可以一步得到内积,即
,无需计算
即可直接得到内积结果,就可以很大程度简化优化的难度,因此核方法诞生了,
即为(正定)核函数;
7.2. 定义
- 核(无需过多关注):若存在函数
使得
,其中
为特征空间,
为全体实数域,则称
为核函数;
- 正定核:对于一个核函数
,若存在非线性变换
(
属于希尔伯特空间,希尔伯特空间指完备的、可能是无限维的、被赋予内积的线性空间),使得
,换言之任意N个样本的Gram矩阵
是半正定的,则称
为正定核函数;
8. 指数族分布
8.1. 背景
- 指数族分布的定义式:
,其中:
为参数向量;
为对数配分函数(log partition function),配分函数表示包含了所有状态信息的函数,常用于归一化等用途,例如将某函数
归一化为概率分布,可以设
,则
可以使
,即被归一化为概率分布。在指数族分布中,
,则
即为对数配方函数;
代表充分统计量,即对于一组数据
,
包含了其所有统计信息,例如
等等;
- 指数族分布的特点(学完概率图模型和变分推断后补)
8.2. 高斯分布的指数族分布推导
- 对于一组符合一维高斯分布的数据,设参数为
,其概率密度函数为:
- 因此可得:
,同时
,
,即得到了一维高斯分布的指数族分布形式;
8.3. 关于对数配分函数的一些结论
- 由于
,可得
;
- 再两边积分可得:
;
- 两边对
求导为:
;
- 因此
- 进一步也可推导得
,推导过程略;
8.4. 最大熵角度解读指数族分布
- 概率的信息量:
;
- 熵的定义:信息量的期望,
;
- 最大熵:令熵值最大的概率分布情况,通常分布越趋向于等可能/均匀分布,熵值越大,因此最大熵也是等可能的量化分析;
- 对于一组离散变量的数据
,其分布未知,但可以用经验分布代替,即
,同时设一向量函数
,则可以对其求期望
,因此可以将最大熵问题设为一个优化问题,即
;
- 使用拉格朗日乘数法求解,
,对
求导得
,令其为0,则解得
,因此当
时,可以令
,
,此时
为指数族分布;
9. 概率图模型
9.1. 背景
- 概率模型的四大法则:
- 加法法则:
;
- 乘法法则:
;
- 链式法则:
;
- 贝叶斯法则:
;
- 加法法则:
- 概率模型的困境:当样本特征维度较高时,计算非常复杂;
- 简化方法:
- 朴素贝叶斯假设:假设特征之间相互独立,则
,但该假设过强,很多时候无法保证成立;
- 马尔可夫假设:假设每个特征变量只与前面的m个特征有关,与其他特征都独立,即
,称为m阶马尔可夫假设,但该假设依然过强,且依赖关系的建设较为随意,不符合真实分布;
- 条件独立性假设:假设特征之间存在一组三个集合,
,三个集合互不相交且无顺序性,使得
,即在给定集合
作为条件的情况下,
与
内变量相互独立,条件独立性假设为了解决朴素贝叶斯假设和马尔可夫假设存在的问题而提出,是概率图模型的理论基础;
- 朴素贝叶斯假设:假设特征之间相互独立,则
- 概率图模型可以由以下分类:
- 表示(Representation):
- 有向图:贝叶斯网络;
- 无向图:马尔可夫网络;
- 高斯图(连续):有高斯贝叶斯网络和高斯马尔可夫网络;
- 推断(Inference):
- 精确推断;
- 近似推断:确定性近似推断——变分推断;随机近似推断(MCMC);
- 学习(Learning):
- 参数学习:完备数据或隐变量学习(EM);
- 结构学习;
- 表示(Representation):
- 概率图模型,又叫贝叶斯网络,常见模型有(后续章节都会介绍):
- 单一变量:朴素贝叶斯;
- 混合变量:高斯混合模型(GMM);
- 时间:
- 马尔可夫链;
- 高斯过程(无限维高斯分布);
- 将时间贝叶斯网络与混合变量结合,即为动态模型:
- 隐马尔可夫模型,离散时间;
- 线性动态系统(LDS):卡曼滤波等(Kalman Filter),连续时间;
- Particle Filter,非高斯,非线性;
- 空间:高斯贝叶斯网络;
9.2. 条件独立性的图结构表示
- 下图是最简单的概率图模型,其概率模型可以写作
,这就是条件独立性用图结构表示的方法,条件变量在父节点,独立变量是同层的无边节点,该过程也被称为因子分解;

- 条件独立性的三种图结构:
- T2T(tail to tail):如下图,概率模型已经写过是
,可以理解为
三个随机变量相互之间可能有联系(如
,此时
也有联系),也可能只有
之间、
之间有联系(如
,此时
没有联系),但一旦
被观测(值已定,不再是随机变量),且
依然是随机变量(刚刚说的第二种情况),则
独立(如果是第一种情况,那
是定值,也可以按照独立处理);

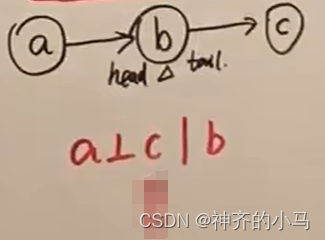
- H2T(head to tail):如下图,概率模型为
,若
被观测,则
独立;
- H2H(head to head):如下图,当
未被观测时,概率模型为
,此时
独立,但如果当
被观测,此时
,
不再独立。值得注意的是,若
的后继子节点被观测,同样会导致
连通,二者不再独立;

- T2T(tail to tail):如下图,概率模型已经写过是
9.3. D-Seperation介绍
- 利用条件独立性的图结构来划分整个概率图模型的集合,即为D划分(D-Seperation)方法,具体来说,图的部分节点分别属于
三个集合,三者互不相交且无顺序性,当满足下面两个条件时,使得
,即在给定集合
作为条件的情况下,
与
内变量相互独立:
- 当
中节点
和
中节点
以T2T或H2T结构存在时,其中间的连通节点
一定在
中;
- 当
中节点
和
中节点
以H2H结构存在时,其中间的连通节点
一定不在
中;
- 当
- 同时可以对某一个节点求其相关节点时,可以用全局节点作为条件求概率密度(设
,即为除了
以外所有节点),即:
只留下了与
相关的节点;
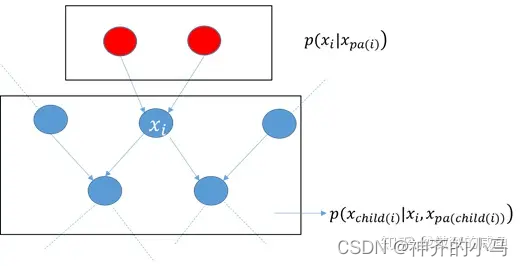
- 与
相关的节点如下图所示,只有
的父节点、子节点及其子节点的其他父节点与
有关,这种关系图被称为马尔可夫毯(Markov Blanket);
9.4. 马尔可夫随机场
- 马尔可夫随机场(Markov random field),又叫概率无向图模型(probabilistic undirected graphical model),每个节点表示一个随机变量,边表示变量之间的相关性,可以用于表示联合概率分布;
- 马尔可夫随机场有三种马尔可夫性质:
- 成对马尔可夫性(Pair Markov Property):设
为除了
和
的其他所有节点,则当
和
没有边连接时,则
;
- 局部马尔可夫性(Local Markov Property):设
为与
连接的所有节点,则
;
- 全局马尔可夫性(Global Markov Property):设
为一个节点的集合,若存在三个集合则
,
,
,其中
中任意节点与
中节点想要连接,都需要经过
中节点,则
;
- 成对马尔可夫性(Pair Markov Property):设
- 团(clique):对于一组节点,如果任意两两之间都存在边连接,则称为一个团,若此时这个团无法再加入新的节点,加入任意一个节点都不能满足两两连通,则称为最大团(类比最大全连通子图);
- Hammersley-Clifford定理:可以将马尔可夫随机场的联合概率分布表示为:
,其中:
为一个权,用于将等号右侧化为概率值:
是图模型中某个最大团
的势函数,势函数的概念由统计物理得来,可以表示为
,
为能函数,如此可以将概率密度化简为:
,该形式满足之前章节的指数族分布的形式,即可以说,马尔可夫随机场等价于指数族分布,等价于最大熵原理;
9.5. 推断(Inference)
- 推断的本质工作就是求概率,或求分布,例如边缘概率、条件概率、后验概率等;
- 推断有两种类型:
- 精确推断:
- Variable Elimination (VE),变量消除法,具体应用见17.3. CRF的边缘概率密度——Smoothing;
- Belief Propagation (BP),又叫Sum-Product算法,由VE改进而来,是精确推断的重要算法,常用于树结构的推断;
- Junction Tree Algorithm,是BP在普遍图结构上的拓展算法;
- 近似推断:
- Loop Belief Propagation,常用于有环图;
- 蒙特卡罗推断(Mente Carlo Inference):例如Importance Sampling,MCMC等;
- variational Inference;
- 精确推断:
10. EM期望最大算法(expectation maximization)
10.1 算法简介
- 概率模型求解时,很多时候数据只有观测变量,因为缺少隐变量而无法求得解析解,也很难通过极大似然估计法对完整的模型参数进行估计;
- EM算法即为含有隐变量的极大似然估计法(或含有隐变量的极大后验概率估计法);
- 举例:有并不均匀的
三个硬币,正面朝上的概率分别为
,首先抛掷
,若正面朝上就抛掷
,若反面朝上就抛掷
,记录最终的抛掷结果为
,但硬币
的抛掷结果作为隐变量未能观测,使得模型参数
不能精准求解;
- 若使用极大似然估计法,则
,忽略了隐变量,但由于
,因此可以使用生成式概率模型的思想,认为
是由
生成的,来对模型参数进行求解
- EM算法分为两步,E步是对
求期望,M步是迭代模型参数
使得期望最大;
10.2 算法收敛性证明
- 首先直接看公式
,其中:
是样本数据,
是隐变量,
是模型参数;
被称为完备数据概率,因为其包含了
的联合概率分布;
是后验概率;
- 这个公式是通过调整参数
,使得
的完备数据的联合概率密度期望最大,因此被称为期望最大算法,核心思路类似于最大似然估计;
- 具体来看,参数是逐步更新的,也就是每次给定当前的参数
,调整
使得完备数据概率的期望最大,并将其赋值给
,即完成了参数更新,直至收敛;
- 接下来看收敛性证明:
- 根据极大似然估计思想,若保证
,则可以保证EM算法的有效性和收敛性;
- 已知
,将两边对
积分:
- 等号左边因为所有变量都与
无关,所以积分值为
;
- 等号右边为
,分别记作
和
,因此等号右边为
;
- 若能保证
,
,则可以保证
,从而保证期望上升;
即为定义(第一行的公式),因此
即为
的最大值,因此
恒成立;
(或者不从KL散度的角度,也可以用
证明),因此
得证;
- 等号左边因为所有变量都与
- 根据极大似然估计思想,若保证
10.3 ELBO+KL散度导出公式
- 已知
,设隐变量
的先验概率分布为
,则:
- 将上式两边对
积分,左边
;
- 右边
,ELBO为证据下界evidence lower bound;
- 当且仅当
时,
,
,此时优化
即为优化
,但这种方法并不保证可以找到
的全局最大值;
10.4 Jensen不等式导出公式
- 根据Jensen不等式,
,
当且仅当
时等号成立;
,两边对
积分,得
,即
,因此
,与ELBO+KL散度得到相同结论;
10.5 广义EM
- 根据上面的推导,EM算法的目标函数
等效为
,当且仅当
时,
达到最大值
;
- 但在某些场景中,后验概率
无法直接求解,因此可以对
进行同步迭代,即为广义EM算法:
- E步:
;
- M步:
;
- E步:
11. 高斯混合模型(Gaussian Mixture Module)
11.1. 模型介绍
- 高斯混合模型即为将某个变量的分布视为多个高斯分布叠加而成;

- 每个样本由各个高斯分布生成的隐变量加权得来,即对每个样本
,都有一组参数
,使得
;
- 注:分布来自于各个高斯分布,但其实某个样本真正的来源只有一个,举例:先抛硬币A,若正面朝上则抛B,反之抛C,记录最终抛的结果,每个样本得到一个记录值,可能来自于B也可能来自于C,B的概率分布为
,C的概率分布为
,A朝上的概率为
,朝下的概率为
,此时最终记录值的概率分布为
,是B和C分别的概率加权叠加,但记录值(或者叫观测值)的真正来源只有1个,B或者C;
11.2. 极大似然估计
- 首先明白,极大似然估计无法求解GMM,这里介绍其中的困难,引出EM算法求解;
;
- 因为log中有连加,且隐变量的概率分布未知,所以这种目标函数无法用极大似然估计求出解析解,需要用迭代逼近的方法计算,例如基于梯度的方法和EM算法;
11.3. EM求解
- E步:
- 首先设隐变量
,表示某个观测样本
来自某个高斯模型
,每个样本的该变量可以表示为一个K维独热向量;
- 列出似然函数
;
- 对数似然函数为
;
- 对其求期望得目标函数:
;
,设
,
,则目标函数的期望
- 首先设隐变量
- M步:
- 对期望函数的各个参数求偏导并使其为0,得到结果(期望简化为E):
;
;
;
- 对期望函数的各个参数求偏导并使其为0,得到结果(期望简化为E):
12. 变分推断(Variational Inference)
12.1. 背景回顾
12.1.1. 两种思路,两种问题
- 概率派:建立概率模型,定义目标函数/损失函数,将问题视为优化问题,得到解析解/数值解(无法得到解析解时,使用梯度下降等方法求得数值解),例如:线性回归、SVM、EM等算法;
- 贝叶斯派:建立概率图模型,求出后验概率
,并根据后验概率进行决策
,将问题视为积分问题,后验概率有时可以精确推断,有时只能进行近似推断,而近似推断的确定性推断即为变分推断,近似推断还有一种随机推断则是MCMC方法;
12.1.2. 推断与生成
- 在概率派思想中,遇到无法观测的隐变量时,模型参数无法通过极大似然估计等方法求出解析解,此时通常使用EM等迭代逼近的方法求出数值解;
- 在贝叶斯派思想中,模型参数
遵循某种概率分布(先验),与隐变量
,观测变量
共同构成概率图模型,相互之间存在相关性和条件独立性,而这个模型中有两种问题:推断与生成:
- 推断:由观测变量的样本集合估计隐变量的概率分布,与EM算法的思路相同,通过最大化
来得到
的分布,即求解
;
- 生成:估计隐变量与观测变量之间的联系,并利用大量随机的隐变量生成新的观测变量(VAE),即求解
;
- 推断:由观测变量的样本集合估计隐变量的概率分布,与EM算法的思路相同,通过最大化
12.2. 公式推导
- 根据贝叶斯派思想,模型参数
也满足某种概率分布,而变分推断是要对参数和隐变量都进行近似推断,因此设
为观测数据样本,
为待推断变量,包含隐变量与模型参数(与EM略有不同);
- 同EM中的推导(这里再写一遍,
,左右对Z求积分得
),ELBO即为变分下界,
;
- 引入平均场理论(mean field theory),设
中存在M个部分,每两个部分两两独立,则有
,则
,此时单独求解某个部分的分布
,则可以固定其他部分,即
;
- 同时
,当其他部分固定,单独求解
时,
;
- 因为
积分的结果是一个关于
的对数概率密度函数,因此可以设
,则变分下界为
,当且仅当
时,ELBO达到最大;
- 如此反复迭代求解,以坐标上升法求出所有参数和隐变量;
12.3. 随机梯度上升变分推断SGVI
12.3.1. 公式推导
- 用另一种思路求解变分推断的隐变量,设
是模型参数,隐变量
遵从某种确定的分布,例如指数族分布,则求解
即为求解分布中的参数
,即
;
- 目标函数无解析解,只能使用迭代逼近的方法求数值解,梯度上升法是一个合适的算法,对目标函数求梯度,(积分和求导符号可以互换位置)
;
- 右边第二项中
与
无关,梯度为0,因此
;
- 因此
,(其中
由上一段推出),由此将目标函数梯度的求解变为一个求期望问题,所以可以通过蒙特卡洛方法求出期望的近似解,从而进行梯度上升迭代计算;
12.3.2. SGVI简化
- 对于SGVI中的梯度求解,常常用到蒙特卡洛方法求期望,但采样过程中有一定概率得到一个接近0的
值,则其中的
会变成一个很小很小的负数,导致采样结果的方差很大,本身梯度上升法就是一种迭代计算的数值解,过程中存在一定偏差,如果采样过程的误差过大则会使得整个算法收敛缓慢,甚至无法得到最优解;
- 为了解决上述问题,也为了简化求梯度的过程,引入一个重参数化机制:
- 原本模型中
是观测变量,
是隐变量,
的分布有参数
,与
无关;
- 重新定义
,设一个新的随机变量
,遵循某种已知分布
,则
,此时
,
;
- 原本模型中
- 则重新推导梯度式:
,此时再采用蒙特卡洛方法则不会出现误差;
13. 马尔可夫链蒙特卡洛法(Markov Chain & Monte Carlo,MCMC)
13.1. 蒙特卡洛方法简介
- 在推断中的近似推断问题中,常常会使用随机近似推断方法,例如最经典的MCMC,核心思想是蒙特卡洛方法,即基于采样的随机近似方法;
- 例如,要计算推断中的期望
,假设随机变量
是连续/无限取值的离散,则对其求期望常常是困难的(连续-积分/无限离散-无穷级数),此时可以随机采样
个样本
,则期望的估计值为
;
- 蒙特卡洛方法中常常使用以下采样方法:
- 概率分布采样:利用变量的概率分布
进行随机数生成,但这个方法仅限概率分布简单的情况;
- Adjection Sampling (接收-拒绝采样法):
- 当随机变量的概率分布
较为复杂时,可以设一个简单分布
,以及寻找一个常数
,使得定义域上的任意
;
- 引入一个新的参数
,称为接收率,其值在0-1之间,且越接近1表示
和
越接近;
- 此时可以从简单分布
中进行采样,每采样一个
的同时也从均匀分布
中采样一个
,当
时,接受采样结果,否则拒绝,需要重新采样;
- 这种采样方法又叫接受-拒绝法,其优点是容易实现,缺点是效率低,如果
所含面积占
所含面积比例过小,则采样很容易被拒绝,需要重新采样,类似的,如果待采样变量维度过高,也很容易采样被拒绝;
- 当随机变量的概率分布
- 重要度采样:同样设一个简单分布
,则原本难算的期望
可以化为另外一个期望,使得原本从
中采样的困难转为从简单分布
中采样,而
称为重要度;
- 概率分布采样:利用变量的概率分布
13.2. 马尔科夫链简介
- 马尔可夫链:
,其中
表示序列上某个步/时间的样本,若一阶马尔可夫,则
,序列上所有随机变量的取值集合相同,被称为状态空间
,
被称为 t 时刻的状态转移函数;
- 这里只讨论一阶马尔可夫链,因为更高阶的马尔可夫链可以推导转换为一阶马尔科夫链,同时若任意的
,有
,则称为时间齐次的马尔可夫链,这里也只讨论时间齐次的马尔科夫链;
- 对于状态空间
全部是离散值的马尔可夫链,其所有的状态转移函数可以写作一个矩阵,即
,称为状态转移矩阵,满足
;
- 基于状态转移函数,马尔可夫链可以表示为,对 t 时刻,取值为 i 的概率为
,为了方便表示,设矩阵
,即为将每一步的计算值存储下来便于后面的计算,其中
被称为初始状态分布,常常是个独热向量,表示马尔可夫链从某个固定状态开始;
- 如果马尔可夫链的状态空间上存在某个分布
,使得
,则称该分布为平稳分布,如果马尔可夫链进入平稳分布,则其接下来的状态分布较为平稳,变化很小,同时一个马尔可夫链可能存在唯一的平稳分布,无穷多个平稳分步,或不存在平稳分布;
- 马尔可夫链的性质:
- 可约性:若对于任意初始状态
和任意状态
,都至少存在一个时刻
,使得
,则说明任意初始状态经过一定时间可以到达任意状态,这种情况称马尔可夫链式不可约的,否则,说明从某个状态出发会永远到不了其他某些状态,这个马尔可夫链称为可约的;
- 周期性:对任意初始状态
,若其经过一定时间后可以回到状态
,且所有最短途径时长
的最大公约数不为1,则称该马尔科夫链具有周期性,否则是非周期的;
- 正常返:定义
表示
,即从状态 j 出发,经过 t 时间首次来到状态 i 的概率,若对任意 j 和 i ,都有
,则称为正常返的马尔科夫链,否则称为不是正常返;
- 可逆性:对于一个马尔可夫链,若存在一种状态分布
,使得任意两个状态
都有
,即
(该式被称作细致平衡方程,detailed balance),则称该马尔可夫链是可逆的;
- 可约性:若对于任意初始状态
- 马尔可夫链性质的定理:
- 不可约且非周期的有限状态马尔可夫链一定有唯一平稳分布存在;
- 不可约且非周期,正常返的马尔可夫链一定有唯一平稳分布存在;
- 遍历定理:对于一个不可约,非周期,正常返的马尔可夫链,设其唯一的平稳分布为
,则对于任意初始状态
,有
,也就是无论初始状态,未来经过无限时刻,状态分布都会趋近于平稳分布,同时对于一个定义在状态空间上的函数
,则
;
- 满足细致平稳方程的分布就是该马尔可夫链的平稳分布;
13.3. MCMC算法
- MCMC适用于随机变量高维且相互不独立,密度函数复杂的情况,在这样的分布中求某个函数的期望
,主要思想是在随机变量的状态空间(所有取值)上定义一个满足便利定理的马尔可夫链,则其平稳分布下函数值的加权平均即为函数的数学期望;
- 因此MCMC计算期望的方法为
,其中 m 是一个较大的数,使得
时的
分布趋于平稳分布,在m之前的遍历称为燃烧期;
- 因为马尔科夫链满足遍历定理,所以随机游走的起点不影响最终结果,因为都会收敛到平稳分布,这个方法比接收-拒绝采样法效率高;
13.3.1. Metropolis-Hastings算法
- 在MCMC算法中,第一个难点是定义一个马尔可夫链用于随机游走,使其满足遍历定理,无论从任何起点出发都将收敛到平稳分布,对于离散分布,要定义状态转移矩阵
,对于连续分布,要定义状态转移核函数
;
- 在MH算法中,可以定义一个建议分布
较为简单易于操作,以及一个接收分布
,则转移核
;
- 通俗理解,MH算法的流程为,定义一个简易分布
,作为转移函数进行随机游走,每次从状态
转移到状态
时,计算接受分布
,并在0-1之间采样随机数
,若
则状态转移成功,
,否则停留在原状态
;
,满足细致平衡方程,因此上面所定义的转移核函数是可逆的,即存在某个分布
使得
,同时该分布为平稳分布;
- Metropolis选择:将建议分布设为可逆分布,即
,此时接收分布简化为
,这是MH算法最初采用的方法,将
定义为一个以
为均值,方差为常数矩阵的正态分布,或是其他在
附近概率较高的简单分布;
- 单分量Metropolis-Hastings算法:当多元变量分布抽样困难时,可以逐步对变量的每一个维度的分量进行抽样,此时建议分布变为
,其中
为t时刻状态的第m个分量,
,类似于每次固定K-1个维度,更新一个维度的过程,同时接受分布
;
13.3.2. 吉布斯抽样
- 满条件分布:对于一个多元概率联合分布
,定义一个条件概率分布
,其中
是变量维度的一个子集,即
,也就是所有维度都在括号里出现,无论在 | 之前还是之后,这个条件概率分布叫做满条件分布,满条件分布满足性质:
,左边计算大大方便,因此可以用满条件分布简化一些计算;
- 吉布斯抽样的方法类似于单分量MH算法,不同的是吉布斯抽样使用
的满条件分布代替建议分布,由于满条件分布比例于原分布的性质,使用满条件分布可以完全模拟原分布
,因此无需MH算法中的接受分布,或者说接受率为1;
14. 隐马尔可夫模型(Hidden Markov Model,HMM)
14.1. 背景
- 概率图模型是贝叶斯派思想的成果,在概率图模型中加入时间的维度,就成为了动态系统(Dynamic Model),其中每个样本是一个时间序列,序列上每个点有观测变量和隐变量,按照隐变量取值类型分为:变量取值离散——HMM;取值连续线性——卡曼滤波(Kalman Filter);取值连续非线性——例子滤波(Particle Filter);
- 贝叶斯派思想的主要问题有 Learning 和 Inference,这些问题也同样是HMM中所关注的,其中Learning是通过样本数据(通常是观测变量
)求模型参数,而Inference又会分为不同形式:
- Decoding:
,通过所有观测变量序列推断所有隐变量序列;
- Probability of Evidence:
,通过模型参数推断所有观测变量序列;
- Filtering:
,通过历史观测信息推断当前时刻隐状态(实时推断,常见于Online计算);
- Smoothing:
,通过所有观测信息推断当前时刻隐状态(复盘式推断,常见于Offline计算);
- Prediction:
,通过历史观测信息推断后续时刻隐状态,也可以预测观测变量;
- Decoding:
14.2. 模型详解
14.2.1. 模型定义
- 先定义观测变量和状态变量的符号:HMM中隐变量取值是离散的,因此可以设观测变量序列为
,隐变量序列为
。
- HMM常用的定义方式为
,其中
为初始状态,
为状态转移矩阵,矩阵中元素
,
为发射矩阵,矩阵中元素
;
- HMM满足两个基本假设:
- n阶齐次马尔可夫性:某个时刻隐状态只与前n个时刻有关,即
;
- 观察独立性:某个时刻观测变量只与当前时刻隐变量有关,即
;
- n阶齐次马尔可夫性:某个时刻隐状态只与前n个时刻有关,即
- HMM的三个基本问题:
- Evaluation:求
;
- Learning:求
;
- Decoding:求
;
- Evaluation:求
14.2.2. Evaluation
- 前向算法:
- 正常求解
,可以对其进行分解:
,其中
,
,因此带入原式可得:
,但其中
的遍历计算量较大,因此需要考虑使用递推的思想简化,即为前向传播算法;
- 设
,只要能求出
,即有
;
的引入需要简化计算,现在推导
与
的递推式:
,由此即可从
一路计算到
,从而完成前向算法;
- 正常求解
- 后向算法:
- 同样是为了求解
而提出,假设已有信息是
时刻的变量,从后往前递推的一种算法;
- 设
,则有
;
- 同样,需要推导递推式:
- 同样是为了求解
14.2.3. Learning
- Learning问题即为求解模型参数的过程,从EM思想入手,EM算法的公式为
,带入HMM的各个变量得到公式:
(因为HMM有时序性,为了避免和时间变量t重复,这里改用s,表示迭代的某个step),其中
,且
,分母的值与
无关,因此式子还可以写作
;
- 易知
,带入公式得
,再分别使用拉格朗日乘子法等方法求解各个变量(推导过程略,简单繁杂,可以自己尝试):
;
;
;
14.2.4. Decoding
- Decoding过程核心任务为通过观测变量的信息计算最有可能的隐状态序列,即
(也和预测问题一起讨论,例如可以预测
);
- 近似算法:
- 近似算法使用贪心算法的思想,在每一步取概率最大的隐状态,得到一个隐状态序列;
- 给定模型
和观测序列
,则时间 t 处在某个状态的概率为
,而最有可能的状态即为
;
- 维特比算法(Viterbi):
- 维特比算法是采用动态规划的方法求解HMM的解码问题;
- 首先定义目标概率值:
,也就是到达 t 时刻的目标隐状态所经过概率最大的路径的概率值(类似于最短路径等问题,这类问题非常适合使用动态规划方法)(此时求出的
只是到达状态
的各个路径的概率中,最大的一个概率值,并不能得到具体的路径);
- 则最大概率路径的递推式为:
;
- 通过递推以及
,可以算得最终时刻各个状态的最大概率,则最终时刻的状态为
;
- 此时还需要另一个递推方法来求出完整的状态序列(路径),因此定义逆推概率
,表示当 t 时刻隐状态是
时,上一个节点
的最可能的状态,即
,依次逆推直至
;
14.2.5. 其他推断任务
- Filtering:公式(简化)为
,可以化简为:
;
- Smoothing:公式为
,同样可以化简为
,又被称为前向后向算法;
- Prediction:公式为
,可以化简为
;
15. 线性动态系统(卡曼滤波,Kalman Filter)
15.1. 概述
15.1.1. 背景介绍
- 变量随时间变化的系统叫做动态系统,其中隐变量取值离散的是隐马尔可夫模型(HMM),而隐变量取值连续的分为线性动态系统和粒子滤波(Particular Filter),前者各变量和变量各时刻满足线性关系和高斯分布,后者则不满足;
- 线性关系:时刻之间:
;变量之间:
;其中
是噪声,在线性动态系统中服从高斯分布;
15.1.2. 模型定义
- 设噪声
,同时设初始状态
,则可以通过高斯分布依次计算
得到所有变量的分布,因此模型参数为
;
- 线性动态系统和HMM一样,也服从一阶齐次马尔可夫假设和观测独立假设(见14.2.1.);
15.2. Filtering
- 首先,filtering公式为
,是一种Online算法,通过 t 时刻及之前的观测变量来推测当前状态,这既是模型求解(Learning)的必要信息,同时也是对prediction
结果的修正(Correction);
- filtering也可以递推求解,推导为:
,其中Prediction可以求解为:
,因此可以通过t-1时刻的filtering计算t时刻的prediction,进而计算t时刻的filtering,循环迭代进行求解;
- 总结来说,Filtering的过程可以写作以下步骤:
- t=1,
,并用上面的公式计算Prediction
;
- t=2,根据上面的递推关系计算
(作为filtering的更新,update,以及prediction的修正,correction)和
(新的prediction);
- ……
- t=T,计算
;
- t=1,
- 在整个计算过程中,Filtering和Prediction的计算结果均为高斯分布,其参数(均值和标准差)可以通过之前时刻的计算结果以及模型参数算出,推导过程参考2. 高斯分布中高斯分布的性质,这里不再详细介绍;
16. 粒子滤波(Particular Filtering)
16.1. 背景介绍
- 在15. 线性动态系统(卡曼滤波)中,可以通过filtering和prediction交替迭代的方法求得隐状态序列,但应对非线性非高斯模型,无法求出解析解,只能通过采样模拟的方法求出近似解,如此便诞生了粒子滤波;
- 粒子滤波应用范围非常之广,且已经产生了许多研究成果和变体,这里只介绍最基本的粒子滤波算法;
16.2. 算法介绍
16.2.1. 重要度采样及针对filtering的改进 —— 序贯重要度采样(Sequential Importance Sampling,SIS)
- 首先回顾重要度采样,给定一个复杂的分布
,需要计算期望
时,直接从
中采样较为困难,此时可以设置一个简单的建议分布
,此时
,采样变得容易;
- 将重要度采样应用于动态系统的filtering问题时,对每个时刻 t 和每个样本
,都需要计算重要度
,而
的计算是复杂的,还要计算N次(N个样本);
- 将filtering问题的计算目标进行调整,由
改为
(同样可以达到目标),此时重要度为
,分别推导分子和分母的递推式,如果可以建立递推关系,则可以简化运算:
- 对于分子,可以推导如下
;
- 对于分母,可以设
满足
;
- 将分子分母带入得
,如此便建立了递推计算关系,可以通过蒙特卡洛的重要度采样方法计算filtering问题;
- 对于分子,可以推导如下
- 为了采样能收敛于真正的期望,需要对重要度进行归一化,即保证
,这也就是为什么递推关系中可以化简常数,只要得到正比的关系即可;
- 上述算法即为基础的粒子滤波算法,其中对状态值的每一次抽样结果
被称为一个粒子;
16.2.2. 重采样
- 在应用上述粒子滤波算法的过程中,很多时候存在粒子退化问题,即只有少数状态拥有真正有效的重要度
,其他大多数状态的重要度接近0,但算法每次都需要对所有
以
的概率抽样,而
与重要度
之间没有关联,这意味着可能有很多情况
较大,
较小,抽样结果充斥着不重要的信息,或是反过来,有效信息在抽样结果中占比很低,这些情况都会使计算资源浪费,模型难以收敛,效果变差等等;
- 重采样的思想用于解决上述问题,具体来说,当使用概率
完成抽样后,计算每个粒子的重要度,并对重要度计算CDF,再在0-1的均匀分布上抽取N个分裂因子
,每个
落在CDF的哪个粒子区间内,就把哪个粒子复制一次(有时也叫粒子分裂);
- 例如,抽样得到的结果为z1,z2,z3(从小到大排列),三者的重要度分别为0.1,0.1,0.8,计算CDF为0-0.1、0.1-0.2、0.8-1.0三段,则需要抽取三个分裂因子,假设为0.15,0.38,0.54,第一个落入z2区间(0.1-0.2),则z2复制一次,另外两个落入z3区间(0.2-0.8),则z3复制两次,通过这个方法尽可能让每次抽样的粒子拥有接近1/N的重要度(或者说重要度高的粒子分裂的次数也多,更加能被有效利用,而重要度低的粒子可以适当舍弃);
- 当样本的维度过高时粒子退化问题将更加可怕,此时重采样的必要性更高;
16.2.3. Sampling-Importance-Resampling(SIR)
- 除了重采样外,还有一种方法可以解决16.2.2.中提到的粒子退化问题,就是设置一个更加合理的
,有一个方法是令
,此时重要度的递推关系为
,这种改进版的粒子滤波再加上重采样,可以进一步提升算法性能,叫做SIR;
- 为什么要令
,其实是逻辑上的考虑,filtering的目标为计算
(或
),而这个问题中粒子滤波的方案是要对
进行采样来计算均值,一个很简单的思想是,在已知
的前提下,
越大的
很多时候越有可能成为真正的状态,因此应该赋予其越高的权重,这就是要设置一个特殊的
的原因,就是为了凑出
,然而这是一个朴素的思想,后人对这个建议分布的取法进行了很多研究,这里只介绍最基本的粒子滤波,因此不做赘述;
17. 条件随机场(Conditional Random Field,CRF)
17.1. 背景
- 机器学习分类模型中,有硬分类和软分类两种主流思想,其中硬分类模型有支持向量机SVM(最大化几何间隔)、感知机PLA(误差驱动优化)、线性判别分析LDA(类间大,类内小)等,通过严格的决策边界来区分多类样本;而软分类模型有逻辑回归(及Softmax回归等)和朴素贝叶斯模型等;
- 同时机器学习分类模型也有概率生成模型和概率判别模型两种思想:
- 软分类中的逻辑回归是概率判别模型,优化思想是最大熵(见8.4.,给定均值和方差而无其他信息时,熵值最大的分布是高斯分布,同时最大熵思想是使模型贴近已有样本,而样本无法提供的信息使其尽量服从高斯分布);
- 朴素贝叶斯是概率生成模型,并从中衍生出了隐马尔可夫模型(可以看做时序版本的朴素贝叶斯,同时认为每个观测变量每个时刻都有一个隐状态,为了求解这个隐状态,引入了齐次马尔可夫假设和观测独立假设);
- 从软分类的概率生成模型和概率判别模型的研究成果中,结合了最大熵思想和隐马尔可夫模型的优点,诞生了最大熵马尔可夫模型(Maximum Entropy Markov Model,MEMM),这是一个概率判别模型,即求解的问题是
,同时是一种新的马尔可夫模型,其引入了一个全局变量,使得观测独立假设被打破,这在实际问题中更加合理,样本信息被更多地利用;

- 上述图中阴影部分为MEMM求解过程的的一个步骤,即
,但这样的条件概率求出以后需要进行归一化才能使其符合概率分布特性(求和为1),这样的操作为局部归一化,但每次归一化时没有考虑全局信息,会导致标签偏差问题(Label Bias Problem),而将MEMM的概率图模型变为无向图即可解决这个问题,因此诞生了条件随机场CRF;
- 标签偏差问题是在Learning问题有效收敛的前提下,decoding任务中出现了明显偏差的现象,因为MEMM和CRF中的隐状态常常是标签(用
表示,例如词性标注中具体词语是观测变量,词性如名词、动词、形容词为隐变量),因此叫做标签偏差问题;
- 举例来说:
- 在经典的John Lafferty论文中的例子是:
- 假如样本数据有15个 r→i→d,5个 r→o→d,忽视发射矩阵,仅考虑状态转移,那么在Learning阶段,理想的概率图模型应该如下图所示,此时在decoding阶段,给定观测变量 r→o→d,得到 i2→i4→i5 的隐变量序列;

- 但如果在o2位置有更多的隐变量取值空间,则Learning阶段可能学习到下图所示的,则在decoding阶段给定观测变量 r→o→d时,会在第一步走向i1的路径,从而得到 i1→i3→i5 的隐变量序列,这显然是不正确的;

- 假如样本数据有15个 r→i→d,5个 r→o→d,忽视发射矩阵,仅考虑状态转移,那么在Learning阶段,理想的概率图模型应该如下图所示,此时在decoding阶段,给定观测变量 r→o→d,得到 i2→i4→i5 的隐变量序列;
- 西湖大学NLP课程中给出例子为:如下图,根据频率统计,d4出现了2次,比d6频率更高,但根据维特比算法求出二者的概率,却是d6比d4概率高,因为l3有两种转移的可能,即便两种可能出现的频率更高(l2→l1有2次,l3→l3有2次),但经过归一化后都为0.5的概率值,而l2只有一种转移的可能,即便出现频率低(只有l2→l2有1次),但经过归一化后概率值依然为1,因此d6算得的概率更高,这种现象本质上是局部归一化导致的;

- Toutanova在论文中也讨论了标签偏差现象的原因,提出有一种情况是发射概率过高,例如下图同样是词性标注问题,Will to fight是句子,是观测变量,NN MODAL TO VB是词性(NN指名词,MODAL指情态动词,TO指to专属词性,VB指动词),而MEMM在decoding任务中需要计算的是
,而因为TO是to的专属词性,因此只要见到t时刻观测变量为to即可直接标注词性为TO,无需纳入前一时刻Will的词性作为考虑,这样的模型Learning阶段会无法学习到NN→TO和MODAL→TO之间的状态转移关系,而事实上情态动词后面是基本不搭配to的,因此对Will的词性出现了标签偏差问题,这样的问题本质上也是对to→TO的发射概率进行了局部归一化所导致;

- 在经典的John Lafferty论文中的例子是:
- 因此CRF将MEMM改为无向图连接,使得局部归一化变为了全局归一化,解决了标签偏差问题,同时打破了齐次马尔可夫假设,使得模型更加有效地利用信息;
17.2. CRF的概率密度函数——Decoding
17.2.1. 无向图模型的概率密度函数
- 团:对于一个无向图,其中某个子图满足各个节点相互连通,则作为原无向图的一个团,而对于一个团,若其无法添加一个新节点使其变为一个更大的团(也不能等于原无向图),则称为最大团;
- 概率因子分解法:
- 对于一个无向图形式的概率图模型,要求解其概率密度函数时,常常用到概率因子分解法,具体来说是找到图模型的所有最大团,对每个最大团求解势函数,相乘并归一化得到概率密度函数;
- 公式:设概率图模型中所有变量集合为
,每个
为一个节点,对图划分得到K个最大团
,每个团的势函数为
,则联合概率密度为
,其中归一化因子
;
- 举例:
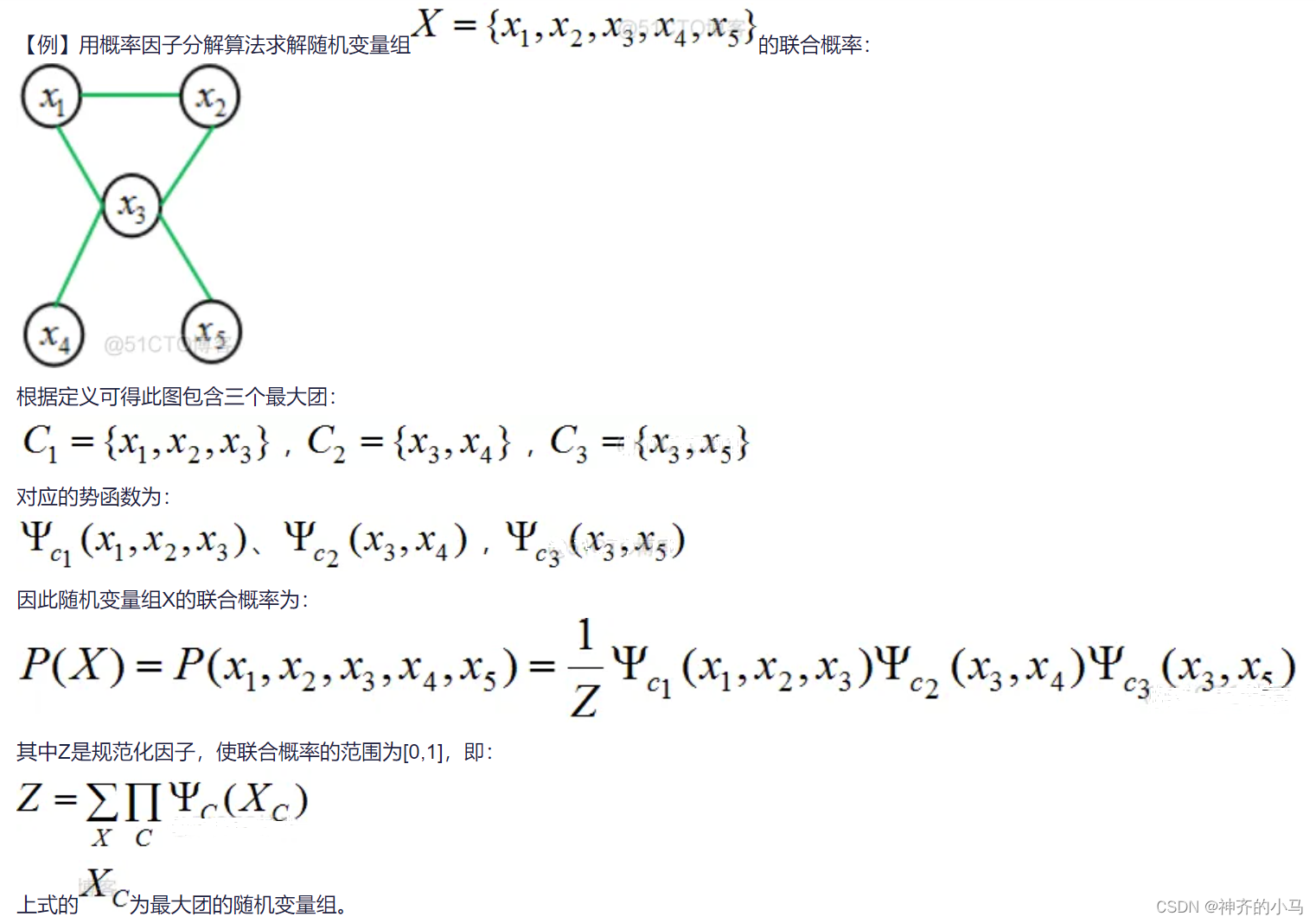
- 可以进一步简化概率因子分解的公式:
,其中
为能量函数,再设
,则
;
17.2.2. CRF的概率密度函数(参数形式)
- 下图是一个典型的CRF概率图,其中每个最大团是
,三个节点组成;

- 由概率因子分解可得,
,因为decoding问题中观测变量
给定,则可以写作
;
- 由于在计算
时,
已知,所以只关注
和
;其中
所表达的信息比较类似HMM中的发射矩阵,而
类似状态转移矩阵,可以通过这个思路来设计合理的函数使得模型更加合理和有效,例如设
,
,其中根据应用场景设计
和
,而将
和
作为可学习参数,这就完成参数形式的概率密度函数;
- 整理参数形式的概率密度函数为:
,其中
,
,
和
同理;
17.3. CRF的边缘概率密度——Smoothing
- 在Decoding中求出概率密度函数
,还需要求解边缘概率密度函数
,先直接写出公式
,这个连乘与积分的计算是非常复杂的(指数级时间复杂度),需要使用动态规划方法递推求解;
- 拆解
,则可以令
,
,因此
;
- 建立递推关系(也是一种前向后向算法):
;
;
17.4. CRF的参数估计——Learning
- CRF的Learning就是根据已有的样本数据来最大化似然函数,即
,等价于求对数似然函数
;
- 对上述最大化似然函数,可以使用梯度上升法逼近数值解,即
,其中
,则
;
- 因为
,其中
可以用前向后向算法求得(见17.3. CRF的边缘概率密度——Smoothing),将该式带入上一步,可以求得
,
也可以同理计算;
18. 高斯网络(Gaussian Network,GN)
18.1. 背景
- 高斯网络也属于概率图模型中的一种,变量离散的概率图模型按照有向和无向分为贝叶斯网络(Bayesian Network,BN)和马尔可夫网络(Markov Network,MN),变量连续的概率图模型是高斯网络,其中假设每个变量都遵循高斯分布,同样按照有向无向分为贝叶斯高斯网络(Gaussian Bayesian Network,GBN)和马尔可夫高斯网络(Gaussian Markov Network,GMN);
- 设总随机变量
是一个p维向量,即高斯网络中有p个节点,则存在总均值
和协方差矩阵
,此时概率密度函数为
;
- 对协方差矩阵
,有
,表示变量之间的(完全)局部独立性,同时
存在精度矩阵
,有
,表示变量之间的条件独立性(原因在18.3. 高斯马尔可夫网络 中有详细介绍);
18.2. 高斯贝叶斯网络(GBN)
- 在贝叶斯网络中,变量的因子分解为
,其中
是父节点变量,而高斯贝叶斯网络中的每个节点
,即每个节点为高斯分布,且与其父节点呈线性关系;
- 用向量表示为
,其中
,
表示变量
与其父节点
的线性关系系数(若不是父节点则为0),
为标准差矩阵,
为一组随机数;
- 通过化简可得
(假设
)可逆,则
;
18.3. 高斯马尔可夫网络(GMN)
- 高斯马尔可夫网络是变量连续的高斯网络中的无向图模型,其建模的思路主要是变量之间的条件独立性,概率密度函数可以统一为
,其中
表示了每个变量(节点)的势函数,而
表示与其相关的变量之间相关性(边)的势函数;
- 将多维高斯分布的概率密度函数写成高斯马尔可夫网络的形式,
,
- 其中对每个变量
,其节点势函数为
,其中
为常数,
为精度矩阵中的元素,
为向量
中的元素;
- 边的势函数为
,表示了节点之间的相关性,因此若
,则两个变量满足条件独立性;
- 其中对每个变量
- 利用精度矩阵
,可以将无向图和多维高斯分布有效联系,建立一个可以建模条件独立性的模型,其中每个变量的边缘概率密度为
,这个结论可以通过2.5. 高斯分布的条件概率分布 中的计算得到;
19. 高斯过程
19.1. 高斯过程简介
- 对于一个无限维的随机变量
,其连续域
是连续的,可以是时间域(动态系统)也可以是空间域(无限维特征),以时间域为例,在时间上的不同点观测得到观测序列,时间点记作
,则该变量的一个样本为一条观测序列
;
- 对于高斯过程中的动态随机变量,其每个时刻的观测值服从当前时刻的一个高斯分布,即
,而整个观测序列服从多维高斯分布
;
- 该高斯过程通常记作
,其中:
为均值函数,
;
为协方差函数,又叫核函数,
;
19.2. 高斯过程回归
19.2.1. 从贝叶斯线性回归到高斯过程回归
- 先回顾贝叶斯线性回归:
- 根据样本数据
,设存在映射系数矩阵,使得
,则可以解得
,其中
(具体推导过程见3.3.4.);
- 进一步地,给定一个新样本
,计算其预测结果
,
,然而贝叶斯线性回归只能解决线性问题,对于现实世界中更多的非线性问题无能为力;
- 根据样本数据
- 为了应对非线性问题,常用的方法是使用一个映射函数,将低维特征映射到高维空间,变成一个高维空间的线性可分问题,我们定义一个非线性转换
,则预测函数变为
,其中
;
- 然而这里又会遇到一个问题,
计算非常困难,需要用到Woodbury Formula公式(公式非常复杂不作介绍,这里只讲简化思路),简化思路如下:
,等式右侧正好是
的均值,也就是期望;
- 用相同方法可以得到
的方差为
;
- 可见均值和方差中出现的
和
都为
的形式,则设核函数:
,则可以带入均值和方差:
- 均值:
,其中
;
- 方差:
;
- 核函数
,化简为了内积的形式,因此简化了上面的计算;
- 均值:
- 上述过程实际上就是高斯过程回归的推导,可以理解为(贝叶斯线性回归+非线性转换+核技巧),而这是高斯过程回归的一个视角,叫权重空间视角,还有另外一个函数空间视角将在后面阐述,两个视角会得到相同结果;
19.2.2. 从权重空间到函数空间
- 根据上述推导结果,
,在已知样本数据
和
的前提下,
都是
的函数,这个很像前面提到的高斯过程
的形式,因此可以从高斯过程来理解;
- 将待预测(待回归)变量设为
,则可以将
和
看做高斯过程,则
,
,因此得到联合概率密度
,再根据多维高斯分布的条件概率密度公式(2.5),求得
,
,与上面推导的权重空间结果相同,但更加简单;
20. 受限玻尔兹曼机(Restricted Bottzmann Machine,RBM)
20.1. 背景
- 在马尔可夫随机场(无向图的概率图模型)中,基于对图划分的最大图进行因子分解,即
,其中势函数
的值需要严格大于0,一种有效的方法为设势函数为指数族分布,即
,则
,这样的概率分布被称为玻尔兹曼分布(吉布斯分布);
- 对于一个变量符合玻尔兹曼分布的无向图模型,将其变量分为观测变量和隐变量,即
,便是玻尔兹曼机(BM),但这样的模型在Inference问题中无法精确推断,利用MCMC进行近似推断又计算量太大,因此需要进行简化,便有了受限玻尔兹曼机(RBM),简化思路为:
和
之间有连接,但各自内部无连接;

20.2. 模型介绍
20.2.1. 模型表示
- 从图的结构角度来表示模型,可以将能量函数写为以下形式:
,因此模型的概率密度函数为:
;
20.2.2. 模型推断
- 在推断中需要求解的是三个问题:
,
和
,前两个计算方法类似,因此只推导一个即可;
- 设
为
中除了
以外的变量,因为受限玻尔兹曼机的假设,内部节点之间满足条件独立性,即
,因此
;
- 由于实际问题中RBM隐变量节点多数是离散变量,这里讨论最简单的0-1分布,其他离散分布形式可以同理计算,因此
;
- 进一步地,将概率密度函数分解为
和
相关的项:
,因此
,同理
,则
;
- 上述推导得到的概率密度函数其实就是Sigmoid函数
,则
,同理可得
进而得
,其中
为
的个数;
- 无论是看RBM的概率图模型,还是概率密度函数与Sigmoid激活函数的相关性,RBM似乎与神经网络都有着很多相近之处,事实上神经网络就是从RBM发展而来,在后面章节中会有所介绍;
- 为了方便推导
,我们将参数
进行分割,即
,则总的概率密度函数中的
;
,继续以
为0-1分布的离散分布为例,
,则
,为了便于化简,令
,则
,其中的累加项非常类似Softplus函数
,该函数图像接近ReLU激活函数(可以看做ReLU的平滑版,相比ReLU没有“死点”,缓解了其梯度消失问题,但计算略微复杂)是最接近脑神经元的激活模型,且一阶导函数为Softmax函数,因此可得
;
25. 近似推断(Approximate Inference)
- 推断的动机
- 推断——即为对原因的追溯,具体表现为对隐变量的推断
;
- 同时推断也是模型学习的需要;
- 推断——即为对原因的追溯,具体表现为对隐变量的推断
- 推断的困难
- 在现实很多问题中,精确推断要么无法做到,要么复杂度指数级增高;
- 对有向图来说,还存在explain away的困难(概率图模型中head2head结构使得本来独立的变量变得相关,其相关关系求解起来很困难);
- 对无向图来说,存在节点之间的mutual interaction的困难;
- 在现实很多问题中,精确推断要么无法做到,要么复杂度指数级增高;
32. 变分自编码器(VAE)
32.1. 模型表示
- VAE是将概率图模型的思路(变分推断)和神经网络相结合的模型;
- 在VAE之前的生成模型中,主流思想是一种autoregression的方法,即一种补全的思想,例如捕捉图像中像素点之间的相关性,使用一个随机的像素生成一整张图,本质上是用观测变量的一个或多个维度生成全部维度;
- VAE则是一种LVM(latent variable models),即引入高阶隐变量,基于高阶隐变量的建模
,使得模型直接从隐变量
中采样即可得到生成的数据,更好地学习到显示的数据分布,十分优雅;
- 要使模型学习到
,就需要计算后验概率
,使其最大化的过程中学习
,但因为隐变量
的维度很高,因此直接计算
非常困难,因此就需要用到变分推断的方法;
- VAE模型可以认为是
的高斯混合模型(GMM),而隐变量
设为服从高斯分布
,实际问题中为了简化,可以设
;
- 对于隐变量到观测变量的生成过程,可以将模型参数化,即
,即每个样本
都有对应一组参数
对应一个高斯分布,而该样本的隐变量服从这个唯一的高斯分布,每个高斯分布的参数都可以用神经网络拟合;
- 因此,VAE模型引入两个假设:
- 预设定隐变量
是个高维标准高斯分布;
- 对于一组模型参数
,
;
- 预设定隐变量
- VAE模型结构也由编码器和解码器组成:
,学习
;
,学习从随机抽取的隐变量
映射到新生成数据的参数;
32.2. 模型训练
- 根据EM算法和变分推断中的推导,对模型参数
进行推断,就是最大化
的迭代过程,同时也是最大化变分下界ELBO的过程,因此模型目标函数即为
;
- 对ELBO的第二项,基于两个假设,可得
,没有需要学习的参数,
,分别用两个神经网络拟合均值和方差的对数(方差恒大于0,其对数的值域是全体实数,更符合神经网络的训练,无需再用激活函数什么的限定),完成编码器的训练;
- 对ELBO的第一项,因为一个样本
对应一个隐变量
,因此
应当是一个尖锐的单峰分布,所以
,无需对所有z求期望,简化了无限维z无法求积分的问题,而最大化
的过程类似于分类/回归任务,输入为Z输出为X,若X服从离散分布则视为分类任务,使用交叉熵作为损失函数,若X服从连续分布则视为回归任务,使用MSE作为损失函数,完成解码器训练;
- 但VAE存在一个问题,当通过编码器得到隐变量
的分布后,从该分布中随机采样得到一个生成的隐变量样本,送入解码器生成数据,但此时编码器的信息会丢失,即采样得到的这个新的
与已知的
解耦,失去了联系,不知道
是从哪个分布中得到的,同时解码器和编码器各自训练,反向传播断开,使得生成效果会很差;
- 为了解决上述问题,使用重参数化技巧,即通过编码器得到某个分布
后,放弃原本的随机采样策略,引入一个误差项
,而新生成的隐变量
,如此反向传播被打通,编码器和解码器可以同步训练,生成效果提升;
























 1033
1033

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








