计算机图形学实验五-直线段的编码裁剪算法（Cohen-SutherLand算法）

敲键盘的敲

已于 2023-08-21 16:21:22 修改

阅读量2.7k

点赞数 4

分类专栏：计算机图形学OpenGL 文章标签：算法 python 机器学习

于 2023-08-21 09:20:32 首次发布

本文链接：https://blog.csdn.net/weixin_53249260/article/details/132401328

版权

计算机图形学OpenGL 专栏收录该内容

8 篇文章

订阅专栏

实验内容	直线段的编码裁剪算法（Cohen-SutherLand算法）；
实验目的	掌握相关算法的原理及实现
实验要求	实现基础代码；图形化交互；其他（可选）：实现NLN直线段裁剪算法；

3.1 Cohen-SutherLand算法实验数据和结果

算法说明与测试

①算法说明

基本思想：对于每条需要裁剪的线段分为三种情况处理：若线段完全在窗口内，则显示该线段；若线段明显在窗口外，则丢弃该线段；若线段不满足上述两种情况，则在交点处把线段分为两段，其中一段完全在窗口外，则弃之，然后对另一段重复上述处理。其实就是一个递归的裁剪过程。
实现方式：编码，即对于直线上任一点(x,y)，根据其坐标所在的区域，赋予一个4位的二进制码，具体编码规则如下：（1）若x<wxl,D0=1,否则D0=0；（2）若x>wxr,D1=1,否则D1=0；（3）若y<wyb,D2=1,否则D2=0；（4）若y>wyt,D3=1,否则D3=0。

线段的裁剪：若code1|code2=0，直线完全在窗口内；若code1&code2≠0，直线则完全在窗口外；若不满足上述两种情况，此时直线既有在窗口内的部分也有在窗口外的部分，取一个窗口外的端点（编码不为0000）为p，根据p的编码从低位开始找编码值为1的地方，确定要求交的窗口边界，求出直线段与相应窗口边界的交点，用交点代替p，重复上述过程，直到找不到位于窗口外的点，算法结束。

②算法设计

首先定义编码函数，对于传入的点的坐标进行编码，方便后续的计算。

然后定义线段裁剪函数，封装裁剪算法，对传入的两个点进行编码，若两个点的编码均为0，直接显示不需裁剪；若两个点的编码都不为0直接拒绝显示；

若以上两种条件不满足，则将线段进行分割，任选一个在矩形区域外的端点和矩形边框相交，将新求出的端点作为一元素重新求解其编码，返回判断是否满足上面的情况，如此进行递归裁剪，直至满足条件绘制线段或者舍弃线段并退出循环。

③算法测试

左图为原图，右图为裁剪后的图，可以看出若绘制的线段在绘制窗口内，不进行裁剪，直接进行绘制。

左图为原图，右图为裁剪后的图，可以看出若绘制的线段在绘制窗口外，不进行裁剪，直接拒绝绘制。

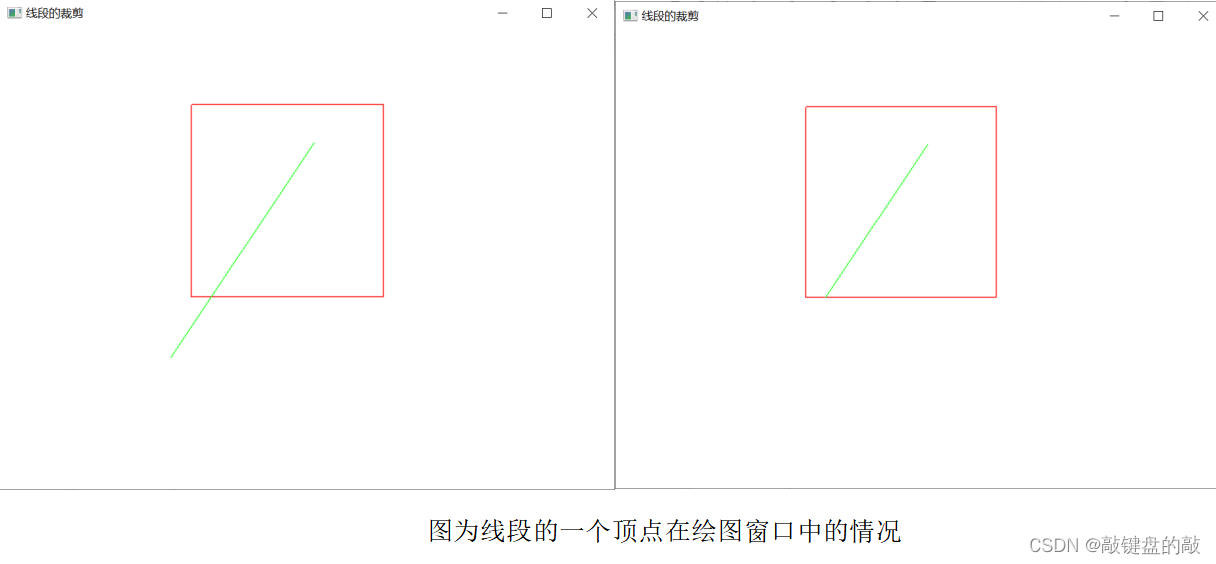
左图为原图，右图为裁剪后的图，可以看出若绘制的线段一部分在绘制窗口外，则对绘图窗口外的线段予以裁剪。

左图为原图，右图为裁剪后的图，可以看出若绘制的线段有两部分在绘制窗口外，则对绘图窗口外的两条线段依次予以裁剪，最后重新绘制图像得到右图。

鼠标交互与键盘交互说明与测试

鼠标交互说明：鼠标的交互体现在初始化绘图窗口后，用户可以用鼠标左键点击的形式选择绘制点，第一次点击确定起始点，后面每鼠标左键点击一次，更新一次终点坐标；由于鼠标左键不能再次更新起点坐标，所以设置当用户点击鼠标右键的时候，将线段的起点终点清空初始化为0，这样用户便可以再次选择线段的起始点了。

键盘交互说明：因为鼠标左右键用于选择点的坐标，为了避免冲突，采用键盘点击的形式进行裁剪操作，设定用户将键盘切换至英文模式下，按下“c”键后进行直线裁剪并重新画图。

NLN直线段裁剪算法实验数据和结果

算法说明：NLN算法通过在裁剪窗口边界创建多个区域，从而避免对一个直线段进行多次裁剪，编码算法中，在找到与裁剪窗口边界的交点之前或完全舍弃该线段之前，必须对一条线段进行多次求交计算，NLN算法则在求交计算前进行更多的区域测试，从而减少求交计算。与前者算法相比，NLN算法的比较次数和除法次数减少。但NLN算法仅用于二维裁剪。

基本思想：对一条线段P0P1来说，其起点P0和终点P1必位于三种区域（角域、边域、内域）之一。下面对三种区域内的线段分别作说明。

P0在内域

连接和裁剪区域的4个角点的直线分别记为LT、RT、LB、RB，通过比较P0P1和这四条直线的斜率，可以确定直线的可见性、直线与区域边界的交点个数及交点所在边界。若斜率位于LT和LB之间，则只需要求P0P1与窗口左边的交点P11，P0P11即为所取线段；若斜率位于LT和RT之间，则只需要求P0P1与窗口上边的交点P11，P0P11即为所取线段；若斜率位于RT和RB之间，则只需要求P0P1与窗口右边的交点P11，P0P11即为所取线段；若斜率位于RB和LB之间，则只需要求P0P1与窗口下边的交点P11，P0P11即为所取线段。

P0在边域

连接和裁剪区域的4个角点的直线分别记为LT、RT、LB、RB，通过比较P0P1和这四条直线的斜率，可以确定直线的可见性、直线与区域边界的交点个数及交点所在边界。以下图为例，若斜率位于LT和RT之间，则只需要求P0P1与窗口左边以及上边的交点P00和P11，P00P11即为所取线段；若斜率位于RT和RB之间，则只需要求P0P1与窗口左边和右边的交点P00和P11，P00P11即为所取线段；若斜率位于RB和LB之间，则只需要求P0P1与窗口左边和下面的交点P00和P11，P00P11即为所取线段；否则直接拒绝绘制。

P0在角域

连接和裁剪区域的4个角点的直线分别记为LT、RT、LB、RB，通过比较P0P1和这四条直线的斜率，可以确定直线的可见性、直线与区域边界的交点个数及交点所在边界。以下图为例，若斜率位于LT和RT之间，则只需要求P0P1与窗口左边以及上边的交点P00和P11，P00P11即为所取线段；若斜率位于RT和LB之间，则只需要求P0P1与窗口左边和右边的交点P00和P11，P00P11即为所取线段；若斜率位于LB和RB之间，则只需要求P0P1与窗口右边和下面的交点P00和P11，P00P11即为所取线段；否则直接拒绝绘制。

算法设计：参考Cohen-SutherLand算法的编码形式，定义编码函数，得到传入的点的坐标，首先判断是否完全可见，完全可见则直接绘制，完全不可见则直接抛弃，以上两种情况均不符合则为部分可见的情况，则开始判断起点所处的区域，针对三个不同的区域进行不同区域的处理，根据不同的斜率值进行不同交点的求解，这里就体现了NLN直线段裁剪算法的优势，通过斜率的判断减少在迭代裁剪过程中求交点的次数。最后更新线段的起点和终点坐标重复上述过程，直至达到完全可见或者完全不可见的情况才停止算法。采用图形化界面的形式，窗口的大小和位置，直线的起点和终点均可由用户自行输入更改，点击ok按钮后即可对线段进行裁剪。