证明 指数分布 的期望和方差

指数分布

指数分布（Exponential Distribution）是一种常见的连续型概率分布，通常用于描述事件之间的时间间隔。假设随机变量 ( X ) 服从参数为 ( \lambda ) 的指数分布，记作

指数分布的概率密度函数（PDF）为：

$$f(x)=\{\begin{array}{ll}\lambda e^{-\lambda x}& x\ge 0\\ 0& x<0\end{array}$$

期望值

期望值（Expectation）表示随机变量的平均值。对于指数分布 ( X )，其期望值 ( \mathbb{E}(X) ) 定义为：

$$\mathbb{E}(X)={\int }_0^{\infty }xf(x)dx$$

代入指数分布的概率密度函数：

$$\mathbb{E}(X)={\int }_0^{\infty }x\lambda e^{-\lambda x}dx$$

将 (\lambda) 提取出来：

$$\mathbb{E}(X)=\lambda {\int }_0^{\infty }x{e}^{-\lambda x}dx$$

为了计算这个积分，我们使用分部积分法。设：

$$u=x,dv=e^{-\lambda x}dx$$

则：

$$du=dx,v=-\frac{1}{\lambda }{e}^{-\lambda x}$$

应用分部积分公式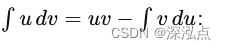

∫ 0 ∞ x e − λ x   d x = − x λ e − λ x ∣ 0 ∞ + ∫ 0 ∞ 1 λ e − λ x   d x \int_{0}^{\infty} x e^{-\lambda x} \, dx = \left. -\frac{x}{\lambda} e^{-\lambda x} \right|_{0}^{\infty} + \int_{0}^{\infty} \frac{1}{\lambda} e^{-\lambda x} \, dx ∫0∞​xe−λxdx=−λx​e