频率域图像增强

之间说过一些空间图像增强的方法，都是通过对像素进行算术逻辑运算得到，很容易理解。但是，傅里叶变换和频率域的图像处理是这个领域必须要掌握的知识。
1.傅里叶变换
主要内容是：不论多复杂的函数，只要是周期的，满足一些条件，就可以写成正弦余弦和的形式。数学的魅力就在于统一化繁为简吧。甚至非周期的函数也可以用正弦余弦乘以加权函数的积分来表示。

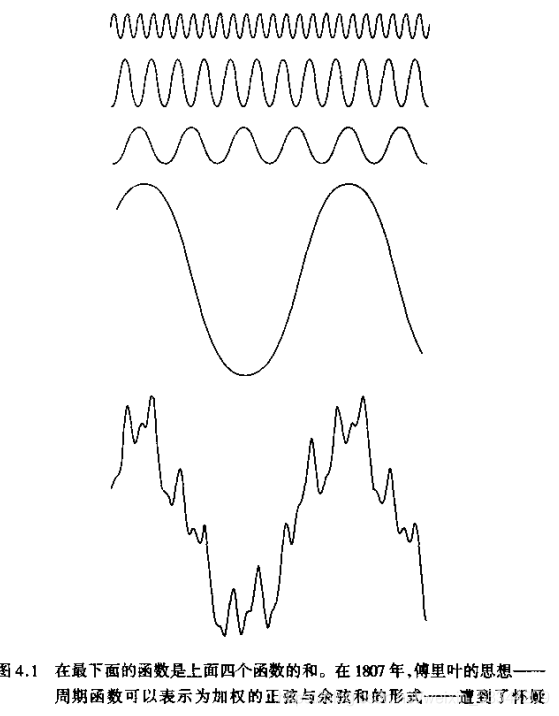
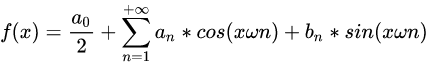
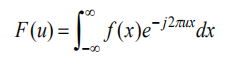
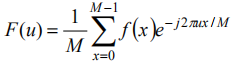
那么，图像和频率的关系是什么呢？
灰度变化缓慢的区域频率低，变化迅速的区域频率高。比如噪声和边缘都是高频，图像轮廓信息是低频，我们所的高通滤波器，低通滤波器，带通滤波器就和这个有关。那么傅里叶变换给我们提供了一个新的角度观察图像。空间域上我们是从灰度分布来看的，而频率域上我们是从灰度的梯度分布来看的。傅里叶变换可以将一个时域信号转换成在不同频率下对应的振幅及相位，但是不是和空间上的点一一对应的。

只不过图像是离散的，有限的，我们可以用离散形式的二维傅里叶变换来处理。二维其实是看成两个一维来处理的。

2.频率域滤波器
频率域滤波能够有效消减周期噪声。
频率域滤波是指对一副图像的离散傅里叶变换进行的滤波处理，然后计算其反变换，得到处理后的空间域结果。

其实就是从频率的角度进行滤波，然后重新得到原图像。
但是滤波的步骤不只是这么简单

我们发现，还需要对原图像进行填充，移动变换中心，再DFT,滤波函数处理，反傅里叶变换，裁剪。

低通滤波器用于图像的平滑模糊，常用的滤波函数有四种
理想低通滤波器


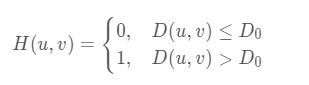
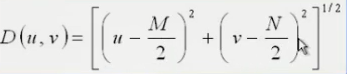
D0是截止频率，D(u,v)是距离频率中心的距离。

布特沃斯低通滤波器

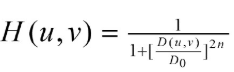
它的特性是连续性衰减，不像理想滤波器那样连续性变化。

其他的滤波器大同小异，函数有变化，不再介绍。