使用最速下降法、共轭梯度法、Barzilar-Borwein方法编程求解下题

今天不熬夜⁠

已于 2023-05-05 17:39:29 修改

阅读量704

点赞数 2

文章标签： python 算法

于 2023-05-05 15:55:00 首次发布

本文链接：https://blog.csdn.net/weixin_53356632/article/details/130508195

版权

文章展示了在n=100的情况下，使用最速下降法、共轭梯度法和Barzilar-Borwein法进行数值优化的过程。通过定义变量、构建目标函数、求导并迭代更新，逐步逼近最小值。代码示例详细解释了每种方法的实现步骤，包括梯度计算、步长优化和迭代条件。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文仅针对n=100，其余情况只需要微调变量数目和x_initial

使用最速下降法

# 定义变量
variables = sp.symbols('x_1:103')

# 定义函数，根据n的取值生成表达式
def get_expression(vaiables):
    fun = 0
    for i in range(len(variables)-2):
        fun_i = (-variables[i]+variables[i+1]+variables[i+2])**2+(variables[i]-variables[i+1]+vaiables[i+2])**2+(variables[i]+variables[i+1]-variables[i+2])**2
        fun += fun_i
    return fun
fun = get_expression(vaiables=variables)
display(fun)


# 定义函数，根据n的取值生成表达式
def get_expression(vaiables):
    fun = 0
    for i in range(len(variables)-2):
        fun_i = (-variables[i]+variables[i+1]+variables[i+2])**2+(variables[i]-variables[i+1]+vaiables[i+2])**2+(variables[i]+variables[i+1]-variables[i+2])**2
        fun += fun_i
    return fun
fun = get_expression(vaiables=variables)
display(fun)



# 对变量求偏导
def get_diff(fun, variable):
    diff_list = []
    for i in range(len(variables)):
        diff_list.append(diff(fun, variable[i]))
    return diff_list
diff_list = get_diff(fun=fun, variable=variables)
diff_list



x_initial = [1,2,3]*34
current_iter_step = 0
# 初始梯度值
grad = [diff_list[i].subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf() for i in range(len(variables))]
grad = [float('{:.4f}'.format(i)) for i in grad]

# 初始目标函数值
current_obj = fun.subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf()

print('初始状态: ','\n','current_iter_step: ',current_iter_step,'\n','x_value:', 
        x_initial,'\n','current_obj:{0:.4f}'.format(current_obj),'\n','grad:',grad,)     


# 定义参数-最大迭代次数以及精度
MaxIter = 1000  
epsilon = 0.001
obj_value = []
# 当梯度的模之和小于阈值时、迭代次数超过限制时，停止迭代
while (sum([grad[i]**2 for i in range(len(grad))])**0.5>= epsilon) and (current_iter_step <= MaxIter):  
    current_iter_step += 1
    # 定义步长
    t = symbols('t')
    # 定义更新后的点
    x_updated = [x_initial[i]-t*grad[i] for i in range(len(variables))]
    # 将更新后的点代入原函数
    Fun_updated = fun.subs({variables[i]:x_updated[i] for i in range(len(variables))})
    # 求解最优步长
    grad_t = diff(Fun_updated, t)
    t_value = solve(grad_t, t)[0]  # solve grad_t == 0
    # 求解更新后的梯度值
    grad = [diff_list[i].subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf() for i in range(len(variables))]
    # 求解更新的点
    x_initial = [x_initial[i]-t_value*grad[i] for i in range(len(variables))]
    # 求解更新后的函数值
    current_obj = fun.subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf()
    obj_value.append(current_obj)
    # 打印迭代过程
    print('current_iter_step: ',current_iter_step,'\n','x_value: ', [float('{:.4f}'.format(i)) for i in x_initial],'\n',
        'grad: ',[float('{:.4f}'.format(i)) for i in grad],'\n','current_obj:{0:.4f}'.format(current_obj),'\n','step_size:{0:.4f}'.format(t_value))


# 绘制迭代过程
plt.plot([i for i in range(current_iter_step)],obj_value, marker='o', c="firebrick", ls='--')
plt.xlabel('iter_step')
plt.ylabel('obj_value')
plt.show()

2. 使用共轭梯度法

import math
from sympy import *
import sympy as sp
from IPython.display import display, Math, Latex
import numpy as np
import matplotlib.pyplot as plt


# 定义变量
variables = sp.symbols('x_1:103')

# 定义函数，根据n的取值生成表达式
def get_expression(vaiables):
    fun = 0
    for i in range(len(variables)-2):
        fun_i = (-variables[i]+variables[i+1]+variables[i+2])**2+(variables[i]-variables[i+1]+vaiables[i+2])**2+(variables[i]+variables[i+1]-variables[i+2])**2
        fun += fun_i
    return fun
fun = get_expression(vaiables=variables)
display(fun)


# 对变量求偏导
def get_diff(fun, variable):
    diff_list = []
    for i in range(len(variables)):
        diff_list.append(diff(fun, variable[i]))
    return diff_list
diff_list = get_diff(fun=fun, variable=variables)
diff_list


x_initial = [1,2,3]*34
current_iter_step = 0
# 初始梯度值
grad_0 = [diff_list[i].subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf() for i in range(len(variables))]

# 初始目标函数值
current_obj = fun.subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf()

print('初始状态: ','\n','current_iter_step: ',current_iter_step,'\n','x_value:', 
        x_initial,'\n','current_obj:{0:.4f}'.format(current_obj),'\n','grad_0:',[float('{:.4f}'.format(i)) for i in grad_0])     


# 第一次迭代--方向为梯度反方向：

t = symbols('t')
    # 定义更新后的点
x_updated = [x_initial[i]-t*grad_0[i] for i in range(len(variables))]
    # 将更新后的点代入原函数
Fun_updated = fun.subs({variables[i]:x_updated[i] for i in range(len(variables))})
    # 求解最优步长
grad_t = diff(Fun_updated, t)
t_value = solve(grad_t, t)[0]  # solve grad_t == 0
    # 求解更新后的梯度值
grad_0 = [diff_list[i].subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf() for i in range(len(variables))]
    # 求解更新的点
x_initial = [x_initial[i]-t_value*grad_0[i] for i in range(len(variables))]
grad_1 = [diff_list[i].subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf() for i in range(len(variables))]
    # 求解更新后的函数值
current_obj = fun.subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf()
print('current_iter_step: ',current_iter_step+1,'\n','x_initial: ', [float('{:.4f}'.format(i)) for i in x_initial],'\n',
        'grad_0: ', [float('{:.4f}'.format(i)) for i in grad_0],'grad_1:',[float('{:.4f}'.format(i)) for i in grad_1],'\n',
        'current_obj:{0:.4f}'.format(current_obj),'\n','step_size:{0:.4f}'.format(t_value))


# 第一次之后的迭代过程：迭代方向改变
# 定义参数-最大迭代次数以及精度
MaxIter = 100  
epsilon = 0.001
obj_value = []
# 当梯度的模之和小于阈值时、迭代次数超过限制时，停止迭代
while (sum([grad_1[i]**2 for i in range(len(grad_1))])**0.5>= epsilon) and (current_iter_step <= MaxIter):  
    current_iter_step += 1

    # 求共轭系数：
    def norm(x):
        return math.sqrt(sum([i**2 for i in x]))
    def beta(grad_0,grad_1):
        return norm(grad_1)**2/norm(grad_0)**2
    beta = beta(grad_0,grad_1)
    # 共轭方向
    def conjugate_direction(grad_0,grad_1):
        return [-grad_1[i]-beta*grad_0[i] for i in range(len(variables))]
    sk = conjugate_direction(grad_0,grad_1)
    # 定义步长
    t = symbols('t')
    # 定义更新后的点
    x_updated = [x_initial[i]+t*sk[i] for i in range(len(variables))]
    # 将更新后的点代入原函数
    Fun_updated = fun.subs({variables[i]:x_updated[i] for i in range(len(variables))})
    # 求解最优步长
    grad_t = diff(Fun_updated, t)
    t_value = solve(grad_t, t)[0]  # solve grad_t == 0
    # 计算当前梯度值
    grad_0 = [diff_list[i].subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf() for i in range(len(variables))]
    # 求解更新的点
    x_initial = [x_initial[i]+t_value*sk[i] for i in range(len(variables))]
    # 求解更新后的函数值
    current_obj = fun.subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf()
    # 计算更新后的梯度值
    grad_1 = [diff_list[i].subs({variables[i]:x_initial[i] for i in range(len(variables))}).evalf() for i in range(len(variables))]
    obj_value.append(current_obj)
    # 打印迭代过程
    print('current_iter_step: ',current_iter_step+1,'\n','x_value: ',x_initial,'\n',
        'grad_1: ',grad_1,'\n','current_obj:',current_obj,'\n','step_size:{0:.4f}'.format(t_value))


# 绘制迭代过程
plt.plot([i for i in range(current_iter_step)],obj_value,marker='o', c="firebrick", ls='--')
plt.xlabel('iter_step')
plt.ylabel('obj_value')
plt.show()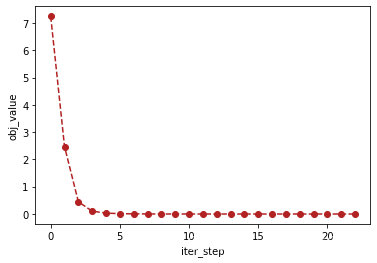

3. 使用Barzilar-Borwein法

可调包实现（前面两种方法也可调用optimtool实现）

import optimtool.unconstrain as ou
import math
from sympy import *
import sympy as sp
from IPython.display import display, Math, Latex
import numpy as np
import matplotlib.pyplot as plt
variables = sp.symbols('x_1:103')


# 定义函数，根据n的取值生成表达式
def get_expression(vaiables):
    fun = 0
    for i in range(len(variables)-2):
        fun_i = (-variables[i]+variables[i+1]+variables[i+2])**2+(variables[i]-variables[i+1]+vaiables[i+2])**2+(variables[i]+variables[i+1]-variables[i+2])**2
        fun += fun_i
    return fun
fun = get_expression(vaiables=variables)
display(fun)
x_0 = (1,2,3)*34
ou.gradient_descent.barzilar_borwein(fun, variables, x_0,epsilon=0.001)