
编者按
本次解读的文章发表于 Operations Research,原文信息:Lu, Y., Chen, Y., Song, M., & Yan, X. (2014). Optimal pricing and inventory control policy with quantity-based price differentiation. Operations Research, 62(3), 512-523.
关键词:随机库存系统;动态定价;多种销售模式;动态规划
问题背景
“买二赠一”、“第二件半价”这类标语是生活中非常简单而常见的促销折扣,本文将这类,对不同购买件数的商品区分定价的销售方案称为批量销售(模式) (quantity sale mode). 将所有单位数量的产品以全价(或正常价格)销售的方案称则为单件销售(模式)(unit sales mode).
此外,动态定价(dynamic pricing)是过去十年中愈发常见的定价方式,批量销售模式则是动态定价的一种新的工具。具体来讲,本文将标准动态定价称为统一定价(策略) (uniform pricing),将动态定价与基于批量销售的组合称为基于批量的定价(策略) (quantity-based pricing ).
本文研究的主题为基于批量的定价和库存控制之间的相互作用,并在以下两个条件的情景中讨论:
- 需求是随机的,并且依赖于价格。
- 补货订单可以在任何时期下达,并产生线性采购成本。
在每个周期初,公司需要完成三项决策:补货批量,销售模式,如果选择了批量销售模式,则需要进一步决定折扣的数额。而在周期末,所有的需求都由库存满足,同时会产生库存成本 (inventory cost) 或者短缺成本 (shortage cost). 公司的最终目标是最大化有限或无限时间跨度下的总利润期望。
那么,本文本质上需要回答三个问题:
- 首先,在动态补货的设置下,最优库存控制策略和最优销售模式是什么?同时采用单件和批量销售模式,还是选择其中之一?
- 其次,如果同时提供两种销售模式,顾客可以通过在批量销售模式中购买m个单位来节省一些钱。我们将这个节省的金额称为批量折扣金额(quantity-discound amount). 批量折扣金额如何依赖于最优库存水平?
- 第三,零售商可能通过提供批量销售模式获得额外利润。基于批量的价格差异化的收益如何依赖于系统参数?
本文为了解答以上问题,构建了两个模型:
- 作者发现,最优库存决策遵循基础库存策略 (base stock policy),而如图1所示的最优销售策略取决于 t t t期的最优订货至水平 y t ∗ y_t^∗ yt∗.
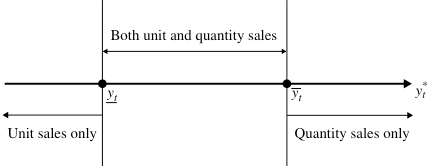
图一:销售模式选择
- 使用随机效用(或估值)模型来刻画需求,可以进一步推导出销售策略的使用条件、最佳价格的单调性性质。
- 只要需要补货,当期最佳策略则一定不是批量销售。
- q 1 ∗ q_1^* q1∗表示商品单价, q 2 ∗ q_2^* q2∗表示批量销售模式下每 m m m个单位商品的总价,则批量销售模式的折扣为 m q 1 ∗ − p 2 ∗ mq_1^* - p_2^* mq1∗−p2∗,可能随着库存水平上升而增加或减少。单调性的方向由效用函数决定。
- q 1 ∗ q_1^* q1∗和 q 2 ∗ q_2^* q2∗都随着库存水平上升而减少,同时 q 2 ∗ − q 1 ∗ q_2^*-q_1^* q2∗−q1∗也随着库存水平上升而减少。
- 是否采用批量销售模式的两种模型的利润差异被称为基于批量的定价策略的价值 (value of quantity-based pricing). 本文证明该值随订购成本的增加而减少,但随着额外 ( m − 1 ) (m-1) (m−1)件产品为顾客产生的增量效用(价值)的增加而增加。
文献综述
过往文献研究主题集中在:库存控制和批量销售模式的折扣(quantity discounts)之间的关系、库存和定价协同问题、动态定价问题。
- 库存控制:现有文献分为两条研究主线,研究买方的经济订货量(economic order quantity), 研究卖方的最佳基于批量的定价策略。本文是后者研究方向的拓展,重要参考文献包括 Altintas, Erhun, and Tayur (2008).
- 库存和定价协同:这类文献研究随机且依赖价格的需求,在有限/无限时间范围内动态地做出定价和库存决策,具体来讲,即需要决策订货量、单位价格。
- 而经典动态定价问下仅研究不同周期的定价策略,不允许补货、基于批量的差异定价。
相比于过去的研究,本文对于动态定价模型拓展以及理论研究有以下贡献:
- 首先,本文将卖方库存控制 (seller’s inventory control) 模型扩展到在随机需求、周期性检查的库存环境中,并对基于批量的定价策略进行建模。
- 其次,本文证明了需求模型所做的三个假设可以通过简单的规律性假设(递增的虚拟价值函数)来统一。
基础模型构建
为了简化参数表达,文章考虑参数稳定的系统,即固定参数不随周期变化的情况(该系统可以扩展到参数不固定的场景)。
对于每一个周期 t = 1 , 2 , ⋯ , n t=1, 2, \cdots, n t=1,2,⋯,n公司在观测到周期初库存水平 x t x_t xt后,确定订单的商品数量,且单位成本为 c c c. 不考虑前置时间 (lead time), 库存立即变为 y t ≥ x t y_t \geq x_t yt≥xt。同时,公司可以选择两种定价 p t = ( p 1 t , p 2 t ) p_t = (p_{1t}, p_{2t}) pt=(p1t,p2t):
- 单件销售模式的价格 p 1 t p_{1t} p1t,
- 批量销售模式价格 p 2 t p_{2t} p2t.
此后,需求被观测到。 t t t周期末,未满足的需求(剩余库存)或积压库存被结转至下一周期。每一周期都由以下几种参数刻画:
- 市场规模 D t D_t Dt. 假设 D t D_t Dt 随时间独立同分布,且 μ 1 = E ( D t ) > 0 \mu_1 = \mathbb{E}(D_t) > 0 μ1=E(Dt)>0.
- 随机市场需求 ξ t = [ λ 1 ( p t ) + m λ 2 ( p t ) ] D t + ε t \xi_t= [\lambda_1(p_t)+ m\lambda_2(p_t)]D_t + \varepsilon_t ξt=[λ1(pt)+mλ2(pt)]Dt+εt, 其中 λ 1 ( p t ) \lambda_1(p_t) λ1(pt), λ 2 ( p t ) \lambda_2(p_t) λ2(pt)分别代表单件销售,批量销售的市场份额 λ 1 + λ 2 ≤ 1 \lambda_1 + \lambda_2 \leq 1 λ1+λ2≤1,
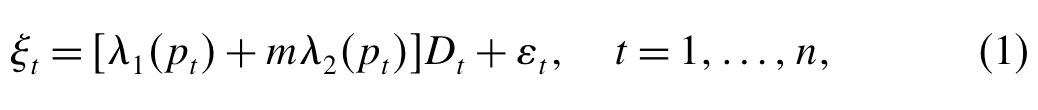
由于这两种模式基本上销售相同的产品,因此它们的需求首先取决于需要该产品的客户数量,然后取决于客户如何在两种模式之间分配需求。因此,销售单位和数量的需求必须具有某种强相关性,这一点由该需求模型的第一部分 λ 1 ( p t ) + m λ 2 ( p t ) \lambda_1(p_t)+ m\lambda_2(p_t) λ1(pt)+mλ2(pt)刻画。
除价格外,其他因素也会影响需求,例如天气和社交活动。同时对价格不敏感的买家数量也是影响需求的不确定因素。因此,模型中采用 ε t = ε 1 t + m ε 2 t \varepsilon_t = \varepsilon_{1t} + m \varepsilon_{2t} εt=ε1t+mε2t来分别表示两种销售模式的需求的不确定性,由此二者也不一定完全相关了。为简化符号表达,价格表达中去掉周期 t t t的下标。
根据常规产品定价的一般规律, λ i ( p i , p j ) \lambda_i(p_i, p_j) λi(pi,pj)随 p i p_i pi减少,随 p j p_j pj增加。文章模仿过往文献进一步假设价格向量 p t p_t pt与市场份额 λ t \lambda_t λt之间存在一一对应关系,因此本文可以将市场份额而不是价格作为决策变量,并且定义出市场份额、价格的可行域:
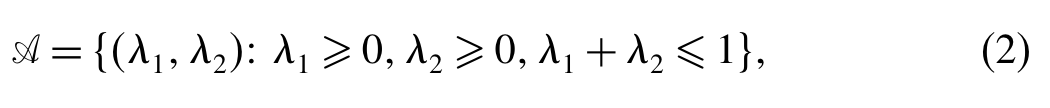
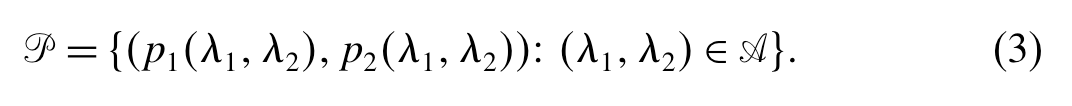
举例说明
- 基于价值的需求模型的收益计算
-
收益期望
假设 V V V表示一单位产品的价值(即效用),其累积分布函数为 G ( p ) G(p) G(p),支撑集为 [ 0 , v ˉ ] [0, v̄] [0,vˉ]. 假设 m m m 单位产品的价值为 a V aV aV, a ∈ ( 1 , m ) a \in(1,m) a∈(1,m). 因此,单位销售模式在 p 1 p_1 p1 的市场份额和批量销售模式在 p 2 p_2 p2 的市场份额可分别推导如下:
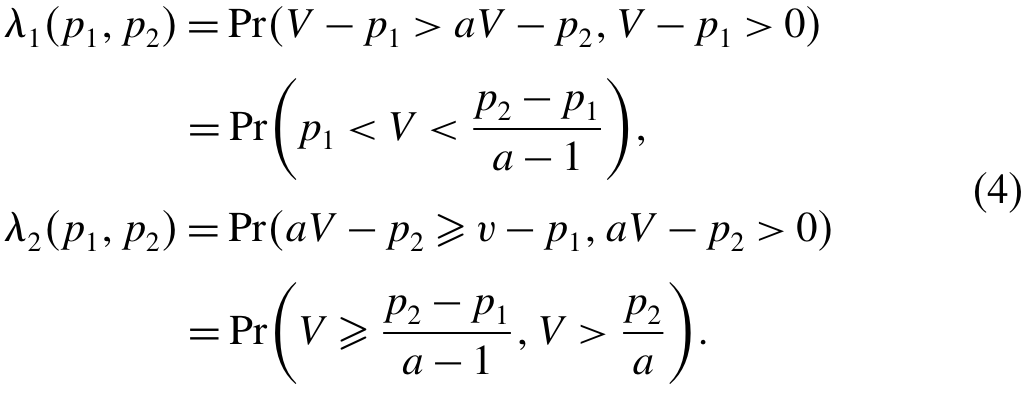
其中 V − p 1 > 0 V-p_1 >0 V−p1>0, a V − p 2 >
-








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








