中国矿业大学计科算法导论菜鸟笔记

南巷_旧人

已于 2022-09-14 17:28:57 修改

阅读量824

点赞数 1

文章标签：算法数据结构

于 2022-09-07 06:27:56 首次发布

本文链接：https://blog.csdn.net/weixin_53711294/article/details/126737331

版权

一算法概述

1.1算法特性

输入、输出、有限性、确定性

1.2算法的描述方法

自然语言、流程图、伪代码、程序设计语言

1.3算法设计要求

正确性、可读性、健壮性、高效性

1.4算法复杂度分析

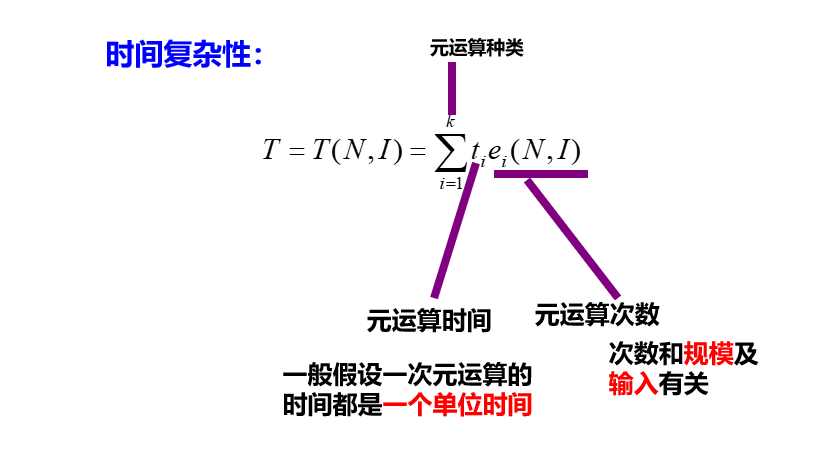
算法的渐进性态

当两个不同算法的阶不同时，只要能确定各个算法的阶，就可判断算法的优劣，无需知道各个算法确切的复杂度表达式。

适用于当N充分大的情况

1.5 NP完全性理论

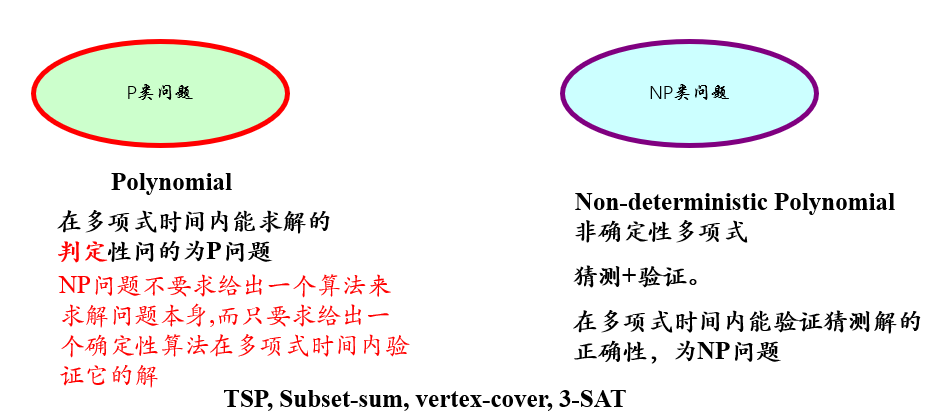
二递归与分治

2.1递归

递归例子

递归函数：用函数自身定义的函数，两要素：边界条件与递归方程。

递归算法：直接或间接调用自身的算法。

2.1.2 Hanoi问题

当n=1时，只要将编号为1的圆盘从柱子A直接移到柱子C上即可；
当n>1时，就需要借助另外一根柱子来移动。将n个圆盘由A移到C上可以分解为以下几个步骤：

(1) 将A柱子上的n-1个圆盘借助C柱子移到B柱子上;

(2) 把A柱子上剩下的一个圆盘从A柱子移到C柱子上;

(3) 最后将剩下的n-1个圆盘借助A柱子从B柱子移到C柱子上。

2.1.3 排列问题

设R={ $r_1,r_2,...,r_n$ }是要进行排列的n个元素， $R_i=R-$ { $r_i$ },集合X中元素的全排列记为Perm(X)。( $r_i$ )Perm(X)表示在全排列Perm(X)的每一个排列前加上前缀得到的排列。设计一个递归算法生成n个元素{ $r_1,r_2,...,r_n$ }的全排列。

关键代码

Template<class T>
void Perm(T list[],int k,int m){
    //递归产生所有前缀是list[0:k-1],且后缀是list[k:m]的全排列
    if(k==m){
        for(int i=0;i<=m;i++) cout<<list[i];
        cout<<"\n";
    }
    else{//还有多个元素，递归产生后缀是list[k:m] 的全排列
        for(int i=k;i<=m;i++){
            swap(list[k],list[i]);
            Perm(list,k+1,m);
            swap(list[k],list[i]);
        }
    }
}

2.1.4 整数划分问题

将正整数n表示成一系列正整数之和： $n=n_1+n_2+...+n_k$ ,其中 $n_1\geq n_2\geq...\geq n_k\geq1,k\geq1$ 。正整数n的这种表示称为正整数n的划分。求正整数n的不同划分个数。

思路

n的划分数=最大加数X等于n的划分个数+最大加数X不大于n-1的划分个数，最大加数X从n开始，逐步变小为n-1,…,1

记q(n,m)为对于n**，最大加数不大于m的划分个数。易得：

q(n,1)=1

q(n,m)=q(n,n) m>n

q(n,m)=1+q(n,n-1) m=n

q(n,m)=q(n-m,m)+q(n,m-1) n>m>1

可得递归公式为：

关键代码

int q(int n,int m){
    if((n<1) || (m<1)) return 0;
    else if((n==1) || (m==1)) return 1;
    else if(n<m) return q(n,n);
    else if(n==m) return 1+q(n,n-1);
    else return q(n,m-1)+q(n-m,m);
}

递归总结

何时使用递归：

1.问题定义或数学定义是递归的，如阶乘和斐波那契数列;

2.数据结构是递归的，如二叉树，链表;

3.问题求解方法是递归的，如Hanoi，数的排列;

递归算法的优缺点：

优点：算法简明，正确性易证明，分析设计的有力工具;

缺点：执行效率低，耗费大量堆栈空间;

2.2分治法

1)将一个难以直接解决的大问题，分割成一些规模较小的子问题;这些子问题互相独立且与原问题相同

2)递归地解子问题

3)将各个子问题的解合并得到原问题的解

时间复杂度分析

迭代方程即可

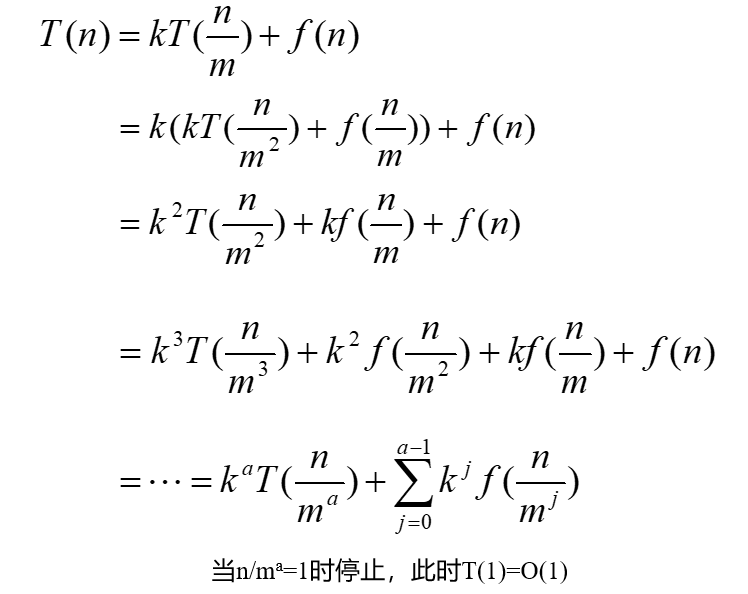
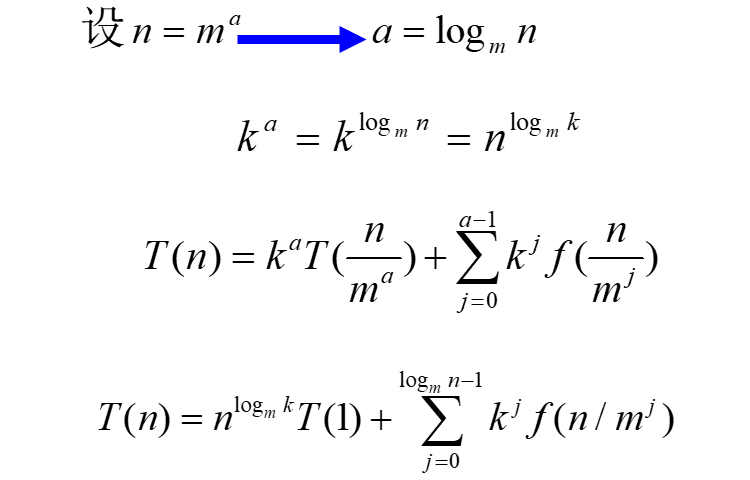
主定理

对形如 $T (n) = a T (n / b) + f (n)$

首先把函数f(n)与函数进行比较，递归方程的解由这两个函数中较大的一个决定：

情况（1），函数 $n^{log_{b}{a}}$ 比函数f(n)更大，则T(n)=O( $n^{log_{b}{a}}$ ) 。

情况（2），函数 $n^{log_{b}{a}}$ 和函数f(n)一样大，则T(n)=O( $n^{log_{b}{a}}log_{2}{n}$ ) 。

情况（3），函数 $n^{log_{b}{a}}$ 比函数f(n)小，则T(n)=O(f(n))。

2.2.2 二分

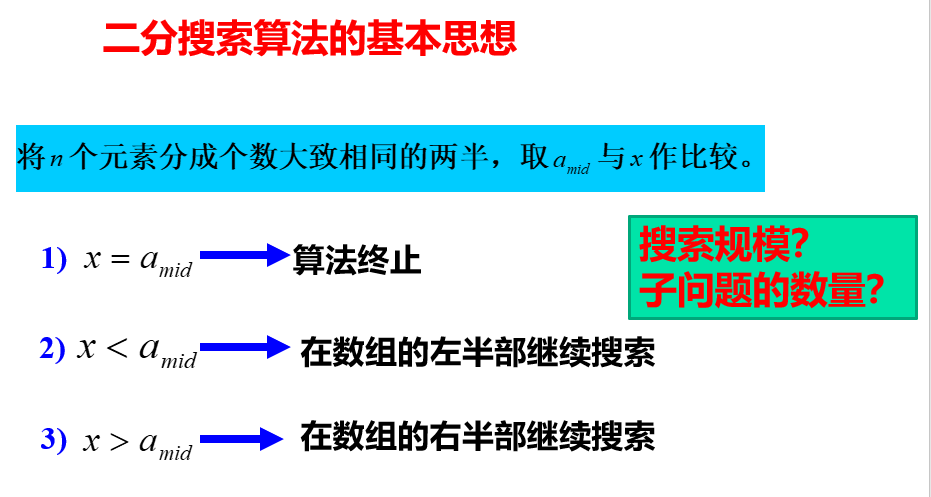
时间复杂度

迭代方程可解出复杂度为O(logn)

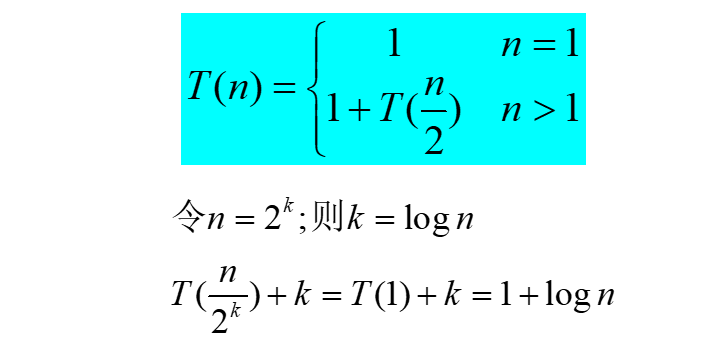
关键代码

int BinarySearch(Type a[],const Type &x,int n){
    int left=0,right=n-1;
    while(left<=right){
        int middle=(left+right)/2;
        if(x==a[middle]) return middle;
        else if(x>a[middle]) left=middle+1;
        else right=middle-1;
	}
    return -1;
}

2.2.3 大整数乘法

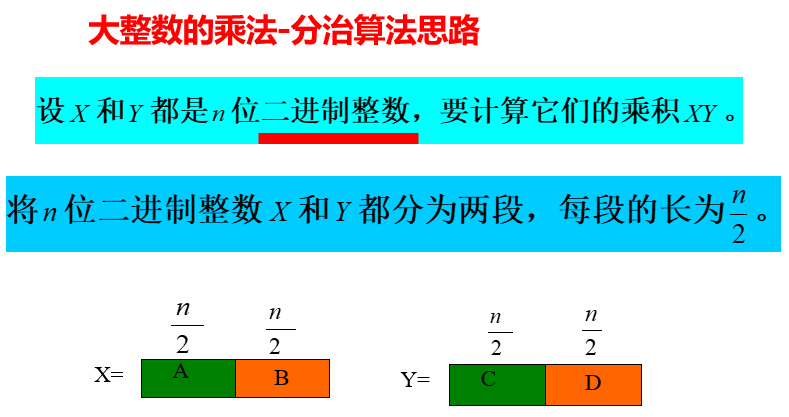
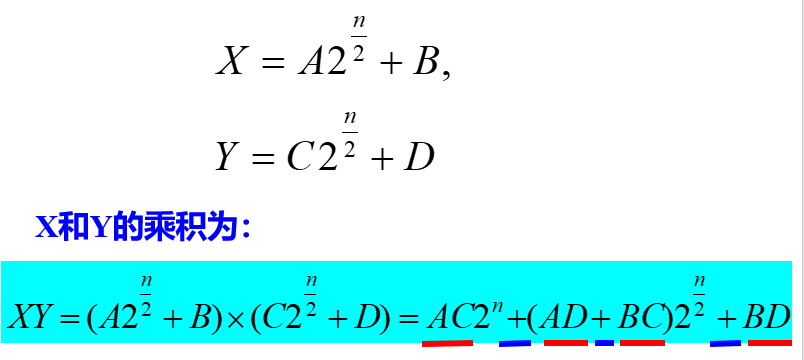
时间复杂度

并不比原算法有效，考虑减少乘法次数，进行式子变换

板子

#include <iostream>
#include <bits/stdc++.h>
#include <math.h>
#include <cstdlib>
#include <stdio.h>
#include <cstring>
using namespace std;
/*位数对齐函数
 *将输入的字符串转换为数字数组(数字数组倒序存储，即高位放在后面，并在数组[0]位置放置数字位的位数)
 *位数对齐：为了方便计算，直接对齐到一个大于两数最大位数的一个2的幂次
 */
int align(char* ch_x,char* ch_y,int& ch_x_length,int& ch_y_length){

    int k = 0;
    int n = pow(2,k);
    while(1){
        if(n>=max(ch_x_length,ch_y_length))
            break;
        ++k;
        n = pow(2,k);
    }

    int i = 0,j = 0;
    if(ch_x_length < n){
        char ch_x_tmp[n];
        for(;i<n;++i){
            if(i < n - ch_x_length)
                ch_x_tmp[i] = '0';
            else
                ch_x_tmp[i] = ch_x[j++];
        }
        strncpy(ch_x,ch_x_tmp,n);
        ch_x_length = n;
    }
    i = 0;
    j = 0;
    if(ch_y_length < n){
        char ch_y_tmp[n];
        for(;i<n;++i){
            if(i < n - ch_y_length)
                ch_y_tmp[i] = '0';
            else
                ch_y_tmp[i] = ch_y[j++];
        }
        strncpy(ch_y,ch_y_tmp,n);
        ch_y_length = n;
    }
    return n;
}
/*大整数加法函数
 *考虑进位
 *并将两数相加和直接补位到指定new_bits位数，存于addxy数组中
 */
void Add(int* x,int* y,int* addxy,int new_bits){//这里应当保证位数的对齐
    for(int i = 1;x[0]+i <= new_bits;++i)
        x[x[0]+i] = 0;
    for(int i = 1;y[0]+i <= new_bits;++i)
        y[y[0]+i] = 0;
    x[0] = new_bits;
    y[0] = new_bits;

    int carry = 0;//进位位

    for(int i = 1;i<=new_bits;++i){
        addxy[i] = (x[i]+y[i]+carry)%10;
        if(x[i]+y[i]+carry>9)
            carry = 1;
        else
            carry = 0;
    }

    if(carry == 1){
        addxy[0] = new_bits+1;//结果长度
        addxy[addxy[0]] = 1;//进位为1
    }
    else
        addxy[0] = new_bits;//结果长度
}
/*大整数减法函数
 *减法位数不会改变
 *考虑大减小和小减大两种情况
 *用数组[0]位的符号表示结果的正负，绝对值为其位数
 */
void Sub(int* x,int* y,int* subxy,int bits){  //x-y  减位 位数不变
    int flag = 0;
    for(int i = bits;i>=1;--i){
        if((x[i]!=0||y[i]!=0)&&(x[i]!=y[i])){
            if(x[i]<y[i])
                flag = 1;
            break;
        }
    }

    if(flag == 0){ //大减小
        int borrow = 0;//借位
        for(int i = 1;i <= bits;++i){
            if(x[i]-y[i]<0){
               x[i+1]--;
                borrow = 1;
            }
            else
                borrow = 0;
            subxy[i] = (10*(borrow) + x[i] - y[i]);
        }
        subxy[0] = bits;

    }
    else{   //小减大
        int borrow = 0;//借位
        for(int i = 1;i <= bits;++i){
            if(y[i]-x[i]<0){
               y[i+1]--;
                borrow = 1;
            }
            else
                borrow = 0;
            subxy[i] = (10*(borrow) + y[i] - x[i]);
        }
        subxy[0] = -bits;
    }

}
/*位数移动函数
 *即扩大10的n次幂
 *这里考虑的是倒序存储的情况
 */
void Move(int* arr,int n){   //正序左移n位  //这里先扩大位数再移位
    for(int i=arr[0];i>=1;--i)
        arr[i+n]= arr[i];
    for(int i = 1;i<=n;++i)
        arr[i] = 0;
    arr[0] += n;
}
/*分治函数
 *将一个大整数分成左右两部分
 */
void Divide(int* arr_1,int* arr_2,int s,int t){ //由arr_1分到arr_2
    int i;
    for(i = 1;i <= t - s;++i)
        arr_2[i] = arr_1[s+i-1];
    arr_2[0] = t -s;
}
/*大整数乘法实现函数
 */
void Multify(int* x,int* y,int* result,const int& n){ //大整数乘法
	//申请空间存放数据四部分
    int* x_div1 = (int *)malloc((n*8+1)*sizeof(int));
    int* x_div2 = (int *)malloc((n*8+1)*sizeof(int));
    int* y_div1 = (int *)malloc((n*8+1)*sizeof(int));
    int* y_div2 = (int *)malloc((n*8+1)*sizeof(int));
    //递归出口
    if(n==1){
        result[1]=x[1]*y[1];
        if(result[1]<=9)
            result[0] = 1;
        else{//存在进位
            result[2]=result[1]/10;
            result[1]%=10;
            result[0] = 2;
        }
        if(x[0]*y[0]<0){ //判断正负
            result[0] = - abs(result[0]);
        }
    }
    else{
    	//分成四部分
        Divide(x,x_div2,1,(n>>1)+1);
        Divide(x,x_div1,n/2+1,n+1);
        Divide(y,y_div2,1,(n/2)+1);
        Divide(y,y_div1,n/2+1,n+1);
        
        int* ac = (int *)malloc((n*32+1)*sizeof(int));//分治结果
        int* bd = (int *)malloc((n*32+1)*sizeof(int));//分治结果
        int* addxy_1 = (int *)malloc((n*32+1)*sizeof(int));//存放加法和
        int* addxy_2 = (int *)malloc((n*32+1)*sizeof(int));//存放加法和
        int* subx = (int *)malloc((n*32+1)*sizeof(int));//存放减法差
        int* suby = (int *)malloc((n*32+1)*sizeof(int));//存放减法差
        int* middle_result_1 = (int *)malloc((n*32+1)*sizeof(int));//中间结果
        int* middle_result_2 = (int *)malloc((n*32+1)*sizeof(int));//中间结果

        Multify(x_div1,y_div1,ac,n/2);//分治
        Multify(x_div2,y_div2,bd,n/2);//分治
        Sub(x_div2,x_div1,subx,n/2);    //B-A
        Sub(y_div1,y_div2,suby,n/2);    //C-D
        Multify(subx,suby,middle_result_1,n/2);//分治
        Add(ac,bd,addxy_1,n*2);
        if(middle_result_1[0] < 0){ //根据正负号 判断接下来的某种操作
            for(int i = 1;abs(middle_result_1[0])+i <= addxy_1[0];++i)
                middle_result_1[middle_result_1[0]+i] = 0;
            Sub(addxy_1,middle_result_1,middle_result_2,n*2);
        }
        else
            Add(addxy_1,middle_result_1,middle_result_2,n*4);

		//下面将所用到的进行退位，排除没用的0空位 因为当前的值的每个位数可能差距太大

        for(int i = abs(middle_result_2[0]);i>=1;--i){
            if(middle_result_2[i]==0)
                continue;
            else{
                middle_result_2[0] = i;
                break;
            }
        }
        for(int i = abs(ac[0]);i>=1;--i){
            if(ac[i]==0)
                continue;
            else{
                ac[0] = i;
                break;
            }
        }
        for(int i = abs(bd[0]);i>=1;--i){
            if(bd[i]==0)
                continue;
            else{
                bd[0] = i;
                break;
            }
        }

        //合并
        Move(middle_result_2,n/2);
        Move(ac,n);
        Add(ac,bd,addxy_2,n*2);
        Add(addxy_2,middle_result_2,result,n*2);

        if(x[0]*y[0]<0) //判断符号
            result[0] = -abs(result[0]);
        else
            result[0] = abs(result[0]);
    }
}
/*main函数
 */


int main(){
    const int maxbits = 1024;
    char ch_x[maxbits];
    char ch_y[maxbits];
    scanf("%s",&ch_x);
    scanf("%s",&ch_y);
    int ch_x_length = strlen(ch_x);
    int ch_y_length = strlen(ch_y);
    int bits = align(ch_x,ch_y,ch_x_length,ch_y_length);//补位
    int* x = (int *)malloc((maxbits*2+1)*sizeof(int));
    int* y = (int *)malloc((maxbits*2+1)*sizeof(int));
    int* addxy = (int *)malloc((maxbits*4+1)*sizeof(int));
    int* subxy = (int *)malloc((maxbits*4+1)*sizeof(int));
    int* result = (int *)malloc((maxbits*8+1)*sizeof(int));
    x[0] = bits;//默认输入的都是正整数
    y[0] = bits;//默认输入的都是正整数
    for(int i = 0;i<bits;++i){ //逆序存储 方便进位
        x[bits-i] = ch_x[i] - '0';
        y[bits-i] = ch_y[i] - '0';
    }
    Multify(x,y,result,bits); //调用函数
    //打印实现
    cout<<"结果:";
    int flag = 0;
    for(int i = abs(result[0]);i>=1;--i){
        if(result[i]!=0){
            flag = i;
            break;
        }
    }
    for(int i = flag;i>=1;--i)
        cout<<result[i];
    return 0;
}

2.2.4 Strassen矩阵乘法

常规的矩阵乘法需要 $n^2$ 的乘法和n的加法，复杂度为O( $n^3$ ).考虑进行如下分治：

将一个规模为n的问题分解为8个规模为n/2的问题，将矩阵A、B 和C 中每一矩阵分块成4个大小相等的子矩阵。当子矩阵的阶大于1时，继续将子矩阵分块，直到子矩阵的阶降为1。

时间复杂度

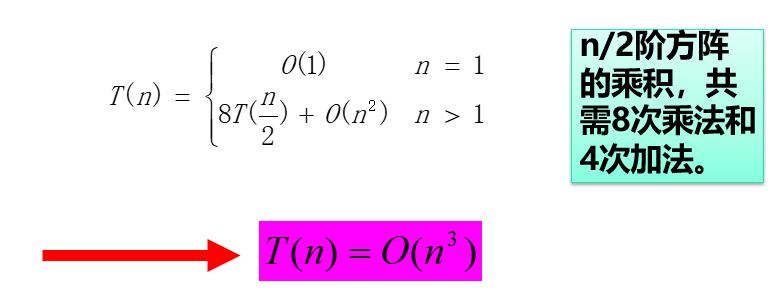
可见时间复杂度仍然为O( $n^3$ )，同大整数乘法思想，对式子进行变换，减少乘法次数。

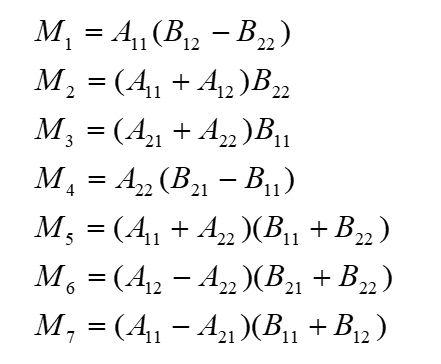
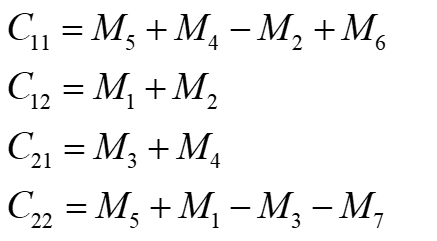
优化后只需要进行七次乘法，也是二阶矩阵所需要的最少乘法次数。算法复杂度如下：

2.2.5 大整数乘法与Strassen矩阵乘法的总结

子问题个数多，划分和综合工作量不太大：

$w(n)=O(n^{log_b{a}})$

利用子问题依赖关系，用某些子问题解的代数表达式表示另一些子问题的解，减少独立计算问题个数n。综合解的工作量可能会增加，但增加的工作量不影响*W(n)*的阶。

2.2.6 棋盘覆盖

在一个 $2^k*2^k$ 个方格组成的棋盘中，恰有一方格残缺,要求用L型骨牌覆盖残缺棋盘上的所有方格且任何2个L型骨牌不得重叠覆盖。残缺方格的位置有 $2^k*2^k$ 种。对任何k≥0，残缺棋盘有 $2^k*2^k$ 种。

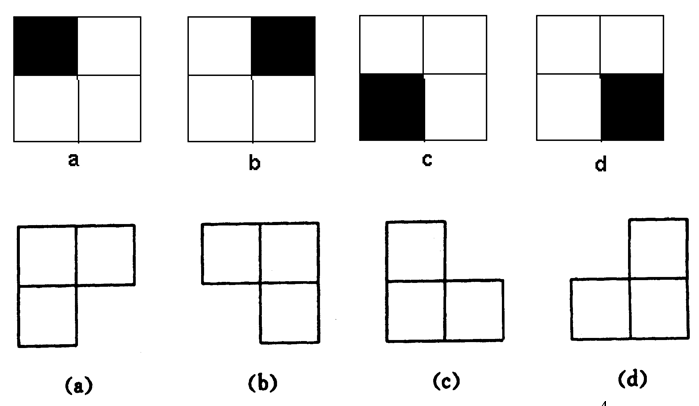
分治思路：将原 $2^k*2^k$ 的方格分解成4个 $2^{k-1}*2^{k-1}$ 的方格，其中只有一个方格有残缺，不符合分治分解的规则，将剩下三个格子，各赋予一个残缺格子，如此递归下去。

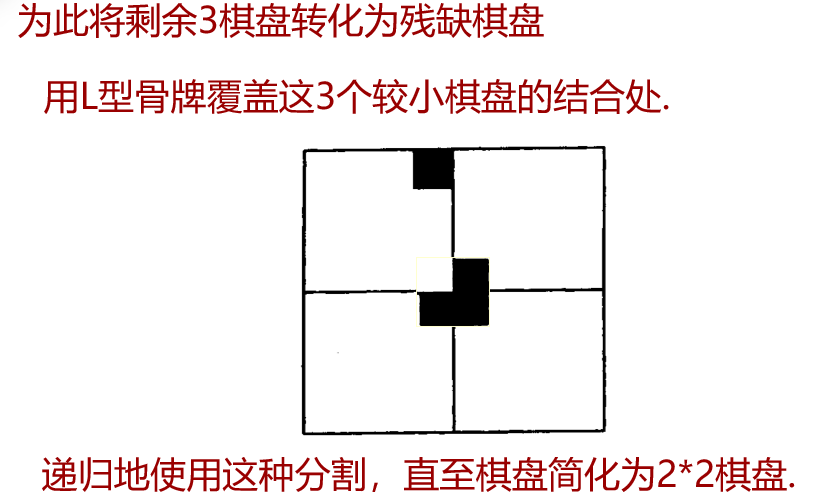
时间复杂度

2.2.7 合并排序

分解：将n个元素分成各含n/2个元素的子序列
解决：用合并排序法将两子序列递归的排序
合并：合并两个已排序的子序列以得到排序结果，对于子序列排序时，其长度为n时，递归结束。

关键代码

template <class T>
void MergeSort(T a[],int left,int right){
    if(left<right){//至少有两个元素
        int i=(left+right)/2;
        MergeSort(a,left,i);
        MergeSort(a,i+1,right);//从a合并到b数组
        Merge(a,b,left,right);//复制回数组a
    }
}

时间复杂度

2.2.8 快速排序

对于输入的子数组 $a [p : r]$ 按以下三个步骤进行排序:

分解：以 $a [p]$ 为基准元素将 $a [p : r]$ 划分成3段 $a [p : q - 1], a [q], a [q + 1 : r]$ ，使 $a [p : q - 1]$ 中任意一个元素小于等于 $a [q]$ ，而 $a [q + 1 : r]$ 中任何一个元素大于等于 $a [q]$ ，下标 $q$ 在划分过程中确定；
递归求解：通过递归调用快速排序算法分别对 $a [p : q - 1]$ 和 $a [q + 1 : r]$ 进行排序；
合并；

关键代码

template <class T>
void QuickSort(T a[],int p,int r){
    if(p<r){
        int q=Partition(a,p,r);//找基准元素a[q]
        QuickSort(a,p,q-1);
        QuickSort(a,q+1,r);
    }
}
int Partition(T a[],int p,int r){
    int i=p,j=r+1;
    T x=a[p];
    while(ture){
        while(a[++i]<x && i<r);
        while(a[--j]>x);
        if(i>=j) break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}
/*
改良，随机选取基准点，以尽量做到规模差不多
*/
template <class Type>
void randomizedQuickSoft(Type a[], int p, int r){  
    if(p<r){
        int q=randomizedPartition(a, p, r)
        randomizedQuickSort(a, p, q-1); //对左半段排序
        randomizedQuickSoft(a, q+1, r); //对右半段排序
     }
}
template <class Type>
int randomizedPartition(Type a[], int p, int r){ 
    int i=random( p, r)
    swap( a[i], a[p] )
    return Partition (a,p,r)
}

时间复杂度

2.2.9 线性时间选择(TOP -K)

给定线性序集中n个元素(无序排列)和一个整数k(1 $\leq$ k $\leq$ n),要求找出这n个元素中第k个小的元素。

直接排序，思路，借鉴选择排序，复杂度 $O (n)$ .
快排，再遍历k，复杂度 $O (k + n l o g n)$ .
分治：

关键代码

template < class Type >
Type RandomizedSelect (Type a[ ], int p,int r, int k){
    if(p==r)return a[p];
     int i=RandomizedPartition(a,p,r),j=i-p+l;
    //统计前半部分元素个数j,  i为基准点
     if(k<=j) return RandomizedSelect(a,p,i,k);
     else return RandomizedSelect(a,i+1,r,k-j); 
}

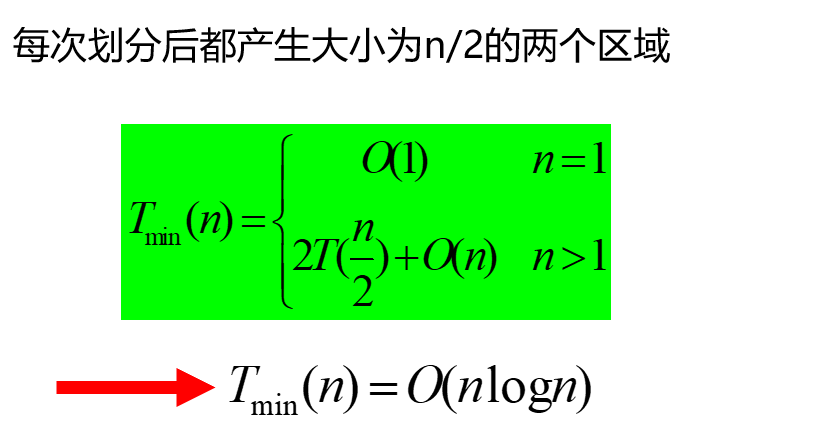
最坏情况下是 $O(n^2)$ 的复杂度，同快排。改良思路：若每次分点总是等分点，每次划分都产生n/2的区域，此时复杂度满足：

时间复杂度

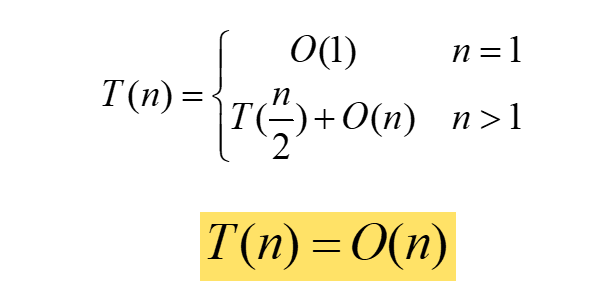
选取基准点，中位数的中位数：

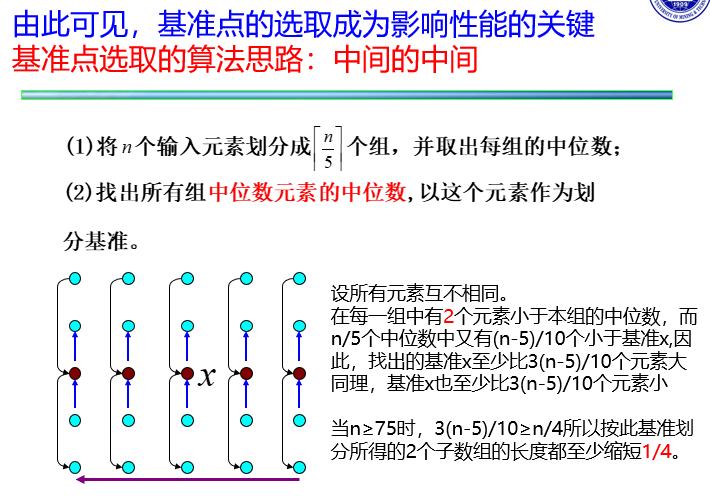
即是每次至少可以减少n/4的规模，可得出复杂度如下：

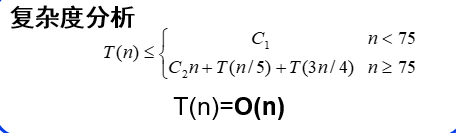
2.2.10 最接近点对问题

在给定平面上n个点,找其中的一对点，使得在n个点组成的所有点对中，该点对的距离最小。

思路：暴力枚举，O( $n^2$ ),从简到难，考虑一维情况；

一维最接近点对问题

考虑将n个点的集合S分成大小近似的两个子集S1和S2，采取分治法求解最近点对，三种情况

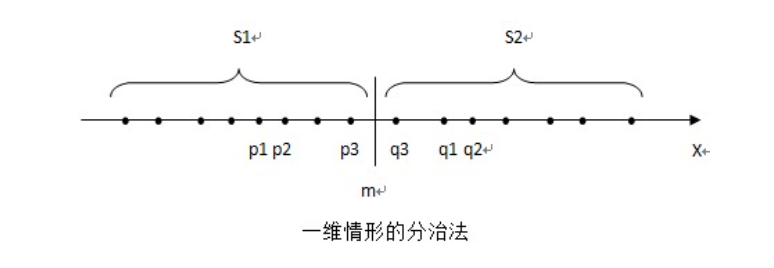
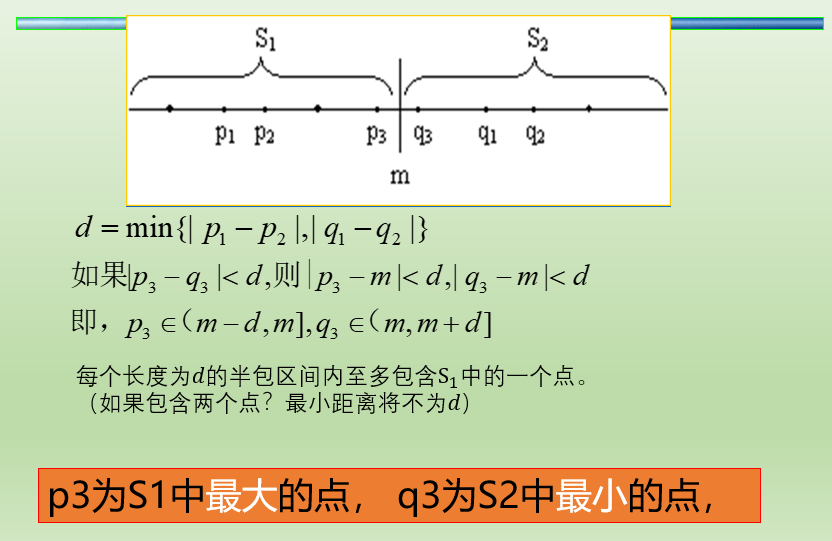
如果最小距离是（p3,q3),简易数学证明可知，p3为左区间最大点，q3为右区间最小值。

算法伪代码

Type CPair1(S, d)
{
	n=|S|;
	if (n<2){d=∞; return false;}
	m=Blum(S); //S各点坐标中位数
	S=>S1+S2;//S1={x|x<=m} S2={x|x>m}
	CPair1(S1, d1);
	CPair1(S2, d2);
	p=max(S1);
	q=min(S2);
	d=min(d1, d2, q-p);
	return d;
}

时间复杂度

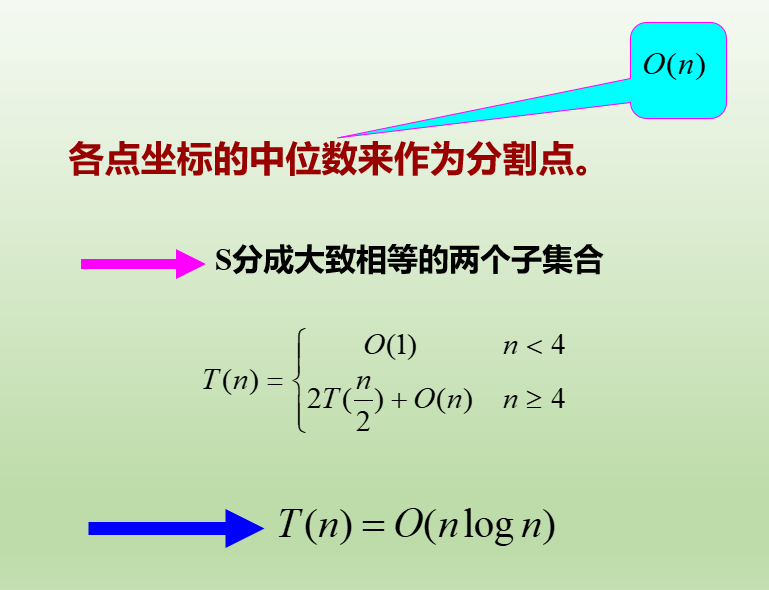
二维最接近点对问题

类比一维，可以选择一条垂线划分集合，让两边点数尽量均衡，可以考虑选取点的x坐标的中位数来作垂线划分；

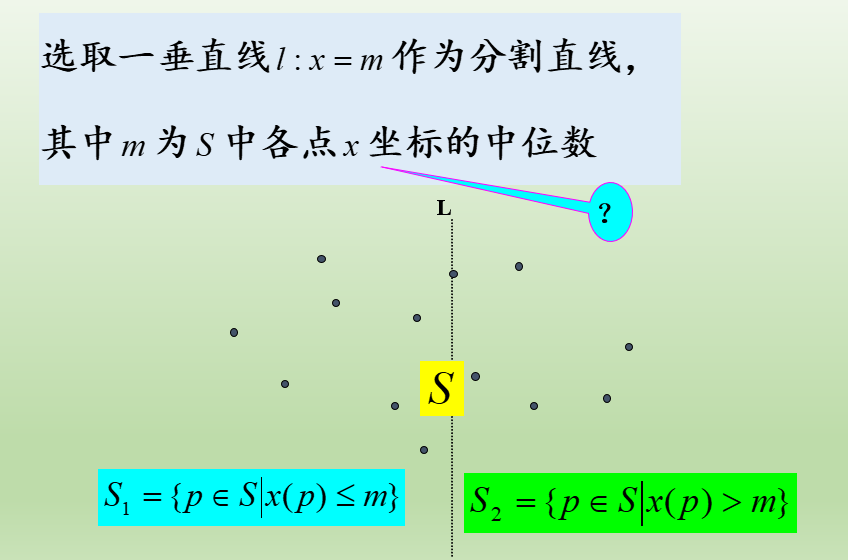
同样和一维类似，最近点对要么在左边，要么在右边，或者两边各一点，类似一维探讨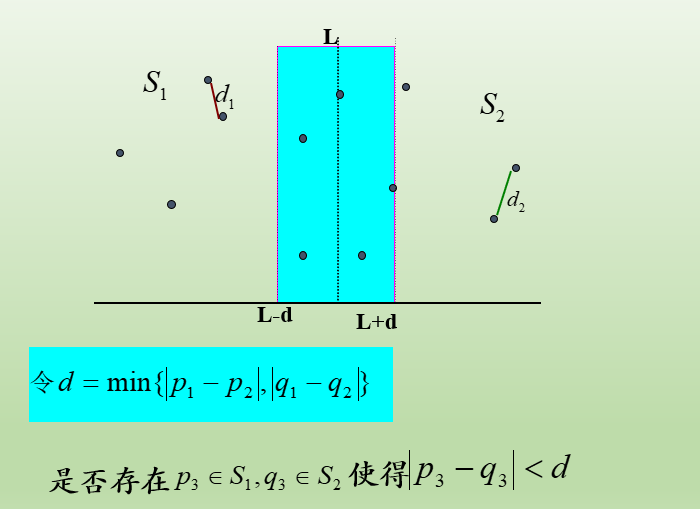

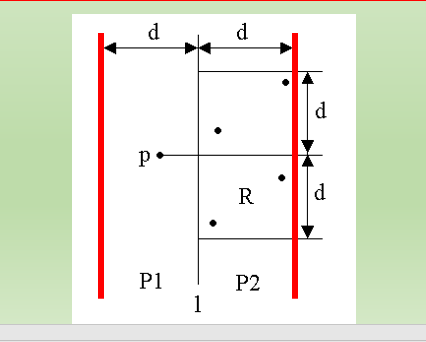
①考虑P1中的任意一点，它若与P2中的点q构成最接近点对的候选者，则必有：distance(p，q)＜d。

②P2中满足条件的点一定落在矩形R中，矩形R的大小为：d×2d。

③由d的定义可知：P2中任何2个点（qi∈S）的距离都不小于d，由此可以推出矩形R中最多只有6个S中的点。

④因此，在分治法的合并步骤中最多只需要检查6×n/2=3n个候选者。

数学证明简单不过多赘述：P2六等分，对角距离

⑤如何确定需要检查的6个点？

可以将p和P2中所有S2的点投影到垂直线L上。
由于能与p点一起构成最接近点对候选者的S2中的点一定在矩形R中。
所以它们在直线 L 上的投影点与 p 在 L 上投影点的距离小于d。
根据上述分析，这种投影点最多只有6个。因此，若将区域P1和P2中所有S中的点按其y坐标排好序。
则：对P1中的所有点，只需一次扫描就可以找出所有候选者。
对排好序的点作一次扫描，可以找出所有最接近点对的候选者。
对P1中每个点，最多只需检查P2中排好序的相继6个点。

伪代码

时间复杂度

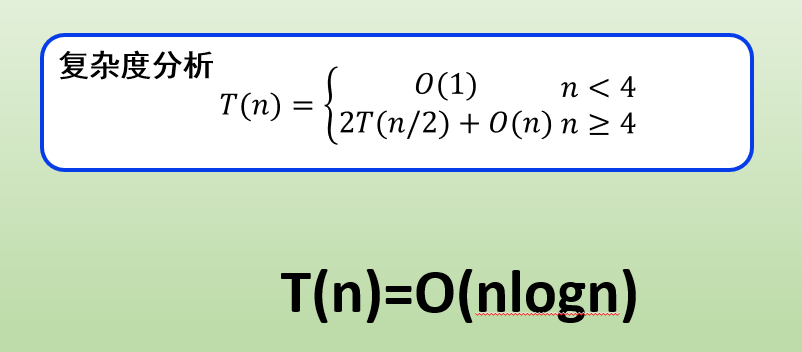
三动态规划(DP)

也就是将结果记录再利用，可类比记忆化搜索，减少重复计算。是一种重要的程序设计手段，其基本思想是在对一个多阶段决策的问题，按照某一顺序，根据每一步所选决策的不同，会引起状态的转移，最后会在变化的状态中获取到一个决策序列。

使用条件：

最优化原理：一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质；
无后效性：将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历史的一个完整总结。这就是无后向性，又称为无后效性。
子问题重叠性

3.1 矩阵连乘

给定n个矩阵 ${A_1,A_2,...,A_n}$ ,其中 $A_i$ 和 $A_{i+1}$ 是可乘的，且 $i = 1, 2, ..., n - 1$ ,如何确定计算矩阵连乘的计算次序，使得计算矩阵连乘积的数乘次数最少？

问题分析：

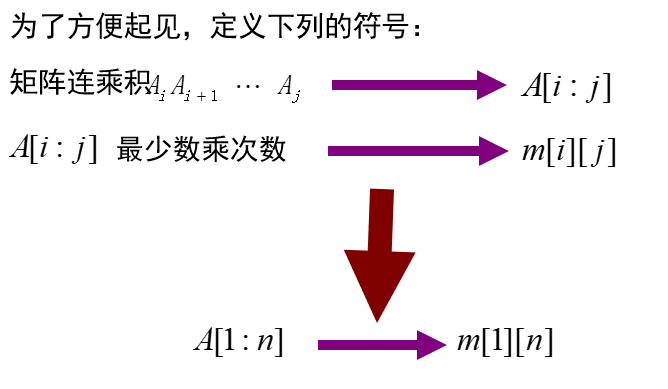
最优子结构证明：

建立转移方程：

很明显可知应该按照矩阵链长度递增的顺序求解，当链长为1时，即是初始化， $m [i] [i] = 0$ ,当链长为2时，$m[i][j]=p_{i-1}p_ip_j.

代码如下：

for(int i=1;i<=n;i++) m[i][i]=0;
for(int r=2;r<=n;r++){//矩阵链长度       
    for(int i=1;i<=n-r+1){
        int j=i+r-1;
        m[i][j]=m[i][i]+m[i+1][j]+p[i-1]*p[i]*p[j];
        s[i][j]=i;//假设最优的位置在i处
        for(int k=i+1;k<=j-1;k++){//遍历
            int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
            if(t<m[i][j]){
                m[i][j]=t;
                s[i][j]=k;
            }
        }
    }
}

时间复杂度明显不过 $O(n^3)$