【菜狗学三维重建】图像质量评价指标（PSNR、SSIM、LPIPS、SILog、MSE、RMSE、MAE）——20250221

目录

指标1：SILog 尺度不变对数误差（越低越好）

    1、全局尺度的不确定性对深度预测的影响

2、尺度不变误差的定义

     3、尺度不变误差的等价形式

指标2：SNR（信噪比）与PSNR（峰值信噪比）（越高越好）

1、SNR 信噪比

2、PSNR 峰值信噪比

指标3：SSIM 结构相似性（越高越好）

1、亮度对比​编辑

2、对比度对比

3、结构相似度

指标4：LPIPS (Learned Perceptual Image Patch Similarity)学习型感知图像块相似性（越低越好）

指标5：MSE（均方误差, Mean Squared Error）（越低越好）

1、特点

2、适用场景

指标6：RMSE（均方根误差, Root Mean Squared Error）（越低越好）

1、特点

2、适用场景

指标7：MAE（平均绝对误差, Mean Absolute Error）（越低越好）

1、特点

2、适用场景

---

指标1：SILog 尺度不变对数误差（越低越好）

        SILog（Scale-Invariant Logarithmic Error）：在计算机视觉中，SIlog是一种用于评估深度估计模型性能的误差度量指标。它通过对深度值取对数，消除不同尺度间的影响，重点衡量深度估计的相对误差。SIlog的值越小，表示模型的深度估计更稳定且与实际更接近。

        Eigen 等人在使用多尺度深度网络 （arXiv） 从单个图像进行深度图预测中提出了此功能，它被广泛用于训练和评估深度预测模型（通常与其他与尺度相关的术语结合使用）。此函数的缺点是预测输出的规模不会影响其量级。以下是论文原文：

指标来源的论文：1406.2283https://arxiv.org/pdf/1406.2283        根据论文关于SILog的描述：

        尺度不变误差（Scale-Invariant Error）在深度预测中的作用和计算方式。其核心思想是：由于三维场景的全局尺度（global scale）在深度预测中存在固有的不确定性，仅靠传统的逐像素误差（如 RMSE）无法准确衡量预测质量，因此提出了一种尺度不变误差来关注深度关系，而不依赖于绝对尺度。

---

    1、全局尺度的不确定性对深度预测的影响

        深度预测存在“尺度歧义”（Scale Ambiguity），即无法确定整个场景的绝对尺度。

        传统的误差度量（如 RMSE）受到尺度误差的影响较大。例如：

• 训练 Make3D 模型在 NYU Depth 数据集上的 RMSE 误差为 0.41（对数空间下）。
• 但如果用真实均值替换预测均值，则误差降到 0.33（减少 20%）。
• 这说明，仅仅找到正确的全局尺度就能显著降低误差。

  ---

  2、尺度不变误差的定义

        这个 α是用于最小化误差的最佳尺度因子，它确保预测和真实值的整体尺度对齐，使得误差不依赖于全局尺度变化。

---

     3、尺度不变误差的等价形式

• 这里强调：尺度不变误差关注的是像素对之间的深度差值，而不是每个像素的绝对深度。
• 换句话说，若预测中的两个像素点的深度关系与真实深度的关系相同（即深度差值匹配），则误差较小。

---

        通过这一误差度量方式，可以在不考虑全局尺度的情况下评估深度预测的质量。它更关注预测的相对深度关系，即物体的远近关系是否正确，而非绝对深度值是否精确。这种方法对尺度歧义问题具有鲁棒性，并能更准确地衡量深度预测性能。以下是定义的函数和使用：

import torch
import torch.nn.functional as F

def silog_loss(pred, target, valid_mask=None, weight=1.0):
    """
    计算 Scale-Invariant Logarithmic (SIlog) Loss。
    
    参数：
    - pred: 预测深度图 (Tensor)，形状 [B, H, W] 或 [B, 1, H, W]
    - target: 真实深度图 (Tensor)，形状 [B, H, W] 或 [B, 1, H, W]
    - valid_mask: (可选) 有效像素掩码，形状 [B, H, W]，用于忽略无效深度值
    - weight: 损失权重系数
    
    返回：
    - 计算得到的 SIlog Loss（标量 Tensor）
    """
    if valid_mask is not None:
        pred = pred[valid_mask]
        target = target[valid_mask]

    # 计算 log 深度误差
    log_diff = torch.log(pred + 1e-6) - torch.log(target + 1e-6)
    
    # 计算第一项：log 误差平方和
    silog1 = torch.mean(log_diff ** 2)
    
    # 计算第二项：均值校正项
    silog2 = (torch.mean(log_diff) ** 2)
    
    # 计算 SIlog Loss
    loss = silog1 - weight * silog2
    return loss

使用示例：

# 创建模拟深度图
pred_depth = torch.rand(1, 1, 256, 256) * 10  # 预测的深度图
gt_depth = torch.rand(1, 1, 256, 256) * 10  # 真实深度图

# 计算 SIlog Loss
loss_value = silog_loss(pred_depth, gt_depth)
print(f"SIlog Loss: {loss_value.item()}")

---

指标2：SNR（信噪比）与PSNR（峰值信噪比）（越高越好）

1、SNR 信噪比

• 定义：SNR 衡量信号的能量相对于噪声的能量的比值，通常用于衡量信号的整体质量。

• 计算公式：

   

  其中：

• 

• 特点：

  • 计算的是整个信号与噪声的比值，没有考虑峰值的概念。
  • 常用于通信、音频、医学信号等领域，衡量信号受到噪声干扰的程度。

2、PSNR 峰值信噪比

• 定义：PSNR 主要用于图像和视频质量评估，衡量失真图像相对于原始图像的质量。

• 计算公式：

  

• 其中：

• 

• 特点：

  • 主要用于衡量图像和视频的重建质量，数值越大表示质量越高。
  • 由于是基于最大像素值计算的，所以比 SNR 更适用于图像质量评估。
  • 对人眼视觉系统的感知不够敏感，因此通常会搭配 SSIM 或 LPIPS 一起使用。

import cv2

# 读取两张图片（确保两张图片大小相同）
img1 = cv2.imread("image1.png")
img2 = cv2.imread("image2.png")

# 计算 PSNR
psnr_value = cv2.PSNR(img1, img2)
print(f"PSNR: {psnr_value} dB")

---

指标3：SSIM 结构相似性（越高越好）

        0-1之间，结构相似性指标（Structural Similarity, SSIM）是一种更为复杂的图像质量评价指标。SSIM认为图像质量不仅取决于像素点间的差异，还与图像结构信息的相似程度有关。SSIM考虑了亮度、对比度和结构三个方面的相似性，是对MSE和PSNR的一个重要补充。

SSIM 适用于：

• 图像质量评估（如压缩、重建、增强等）。
• 计算机视觉和深度学习任务（如图像生成、去噪、超分辨率等）。

---

1、亮度对比

---

2、对比度对比

---

3、结构相似度

from skimage.metrics import structural_similarity as ssim
import cv2

# 读取两张灰度图像
img1 = cv2.imread("image1.png", cv2.IMREAD_GRAYSCALE)
img2 = cv2.imread("image2.png", cv2.IMREAD_GRAYSCALE)

# 计算 SSIM
ssim_value, _ = ssim(img1, img2, full=True)
print(f"SSIM: {ssim_value}")

---

指标4：LPIPS (Learned Perceptual Image Patch Similarity)学习型感知图像块相似性（越低越好）

        是一种 基于深度学习的感知相似度度量，用于衡量两幅图像之间的感知差异。它弥补了 PSNR、SSIM 等传统指标 不能准确反映人眼感知质量的问题，广泛用于图像生成、超分辨率、去噪等任务的质量评估。

        LPIPS 利用预训练深度卷积神经网络（如 VGG、AlexNet、SqueezeNet） 提取图像的特征，并计算它们在高维感知空间中的距离。

        LPIPS的设计灵感来自于人眼对图像的感知，它通过学习一个神经网络模型来近似人类感知的视觉相似性。该模型使用卷积神经网络（CNN）对图像的局部补丁进行特征提取，并计算补丁之间的相似性得分。

具体而言，LPIPS的计算过程如下：

1. 使用预训练的CNN模型（通常是基于深度学习的图像分类模型）提取原始图像和重建图像的特征表示。

2. 将提取的特征表示作为输入，通过一个距离度量函数计算图像之间的相似性得分。

3. 相似性得分表示图像之间在感知上的差异，数值越小表示图像之间的感知差异越小，图像质量越好。

        LPIPS的得分范围通常是0到1之间，数值越小表示图像的感知质量越高。

        与传统的图像质量评估指标（如PSNR和SSIM）相比，LPIPS更加注重于人眼感知的因素，能够更好地捕捉到图像之间的感知差异。它在图像生成、图像编辑等任务中被广泛应用，特别适用于需要考虑感知质量的场景。

        需要注意的是，LPIPS是一种基于学习的指标，它的性能受到所使用的CNN模型和训练数据的影响。因此，在使用LPIPS进行图像质量评估时，需要使用与训练模型相似的数据集和预训练模型，以保证评估结果的准确性和可靠性。

import lpips
import torch
import torchvision.transforms as transforms
from PIL import Image

# 加载 LPIPS 计算器（默认使用 VGG）
lpips_loss = lpips.LPIPS(net='vgg')

# 读取两张图像并转换为张量
transform = transforms.Compose([transforms.Resize((256, 256)), transforms.ToTensor()])
img1 = transform(Image.open("image1.png")).unsqueeze(0)  # 添加 batch 维度
img2 = transform(Image.open("image2.png")).unsqueeze(0)

# 计算 LPIPS 距离
distance = lpips_loss(img1, img2)
print(f"LPIPS 距离: {distance.item()}")

---

指标5：MSE（均方误差, Mean Squared Error）（越低越好）

MSE 衡量的是预测值与真实值之间的均方误差，其公式为：

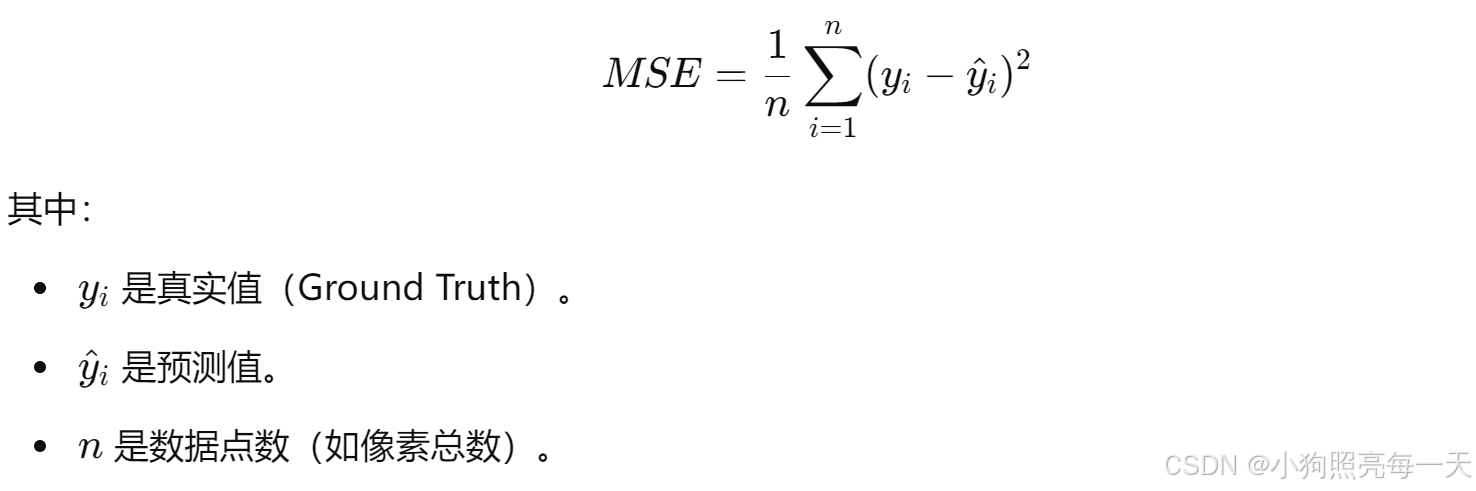
1、特点

✅ 对大误差敏感，因为误差平方放大会放大极端值的影响。
✅ 适用于连续变量（如图像重建、深度预测）。
❌ 误差是平方单位，难以直接解释。
❌ 对离群点敏感，可能导致模型过拟合。

2、适用场景

• 适用于 无噪声或噪声较小的任务，比如 3D 形状重建、图像去噪、超分辨率等。
• 在 误差平方更符合应用需求时（如需要对大误差进行更严重的惩罚）。

import numpy as np

def compute_mse(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

# 示例数据
y_true = np.array([3, -0.5, 2, 7])
y_pred = np.array([2.5, 0.0, 2, 8])

mse_value = compute_mse(y_true, y_pred)
print(f"MSE: {mse_value}")

---

指标6：RMSE（均方根误差, Root Mean Squared Error）（越低越好）

1、特点

✅ 单位与原始数据相同，直观易理解。
✅ 仍然对大误差敏感，但比 MSE 更直观。
❌ 仍然受极端值影响（因为是 MSE 的平方根）。

2、适用场景

• 需要误差单位直观可解释（与原像素或深度值一致）。
• 误差平方根更符合应用需求，如 3D 形状评估、点云误差计算。

def compute_rmse(y_true, y_pred):
    return np.sqrt(np.mean((y_true - y_pred) ** 2))

rmse_value = compute_rmse(y_true, y_pred)
print(f"RMSE: {rmse_value}")

---

指标7：MAE（平均绝对误差, Mean Absolute Error）（越低越好）

1、特点

✅ 对离群点不敏感，比 MSE/RMSE 更鲁棒。
✅ 误差的单位与像素或数值一致，易于解释。
❌ 对大误差没有额外的惩罚，可能导致某些误差较大的点未被充分优化。

2、适用场景

• 适用于数据中可能存在噪声或离群点的任务（如深度预测、3D 重建误差评估）。
• 当误差的实际大小更重要时，而不是对大误差施加额外权重（如医疗影像分析）。

def compute_mae(y_true, y_pred):
    return np.mean(np.abs(y_true - y_pred))

mae_value = compute_mae(y_true, y_pred)
print(f"MAE: {mae_value}")

---

——20250221

小狗照亮每一天