第二周：机器学习+pytorch

线性回归补充

特征缩放

在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。

以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-2000平方英尺，而房间数量的值则是0-5，以两个参数分别为横纵坐标绘制代价函数的等高线图像，可以看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

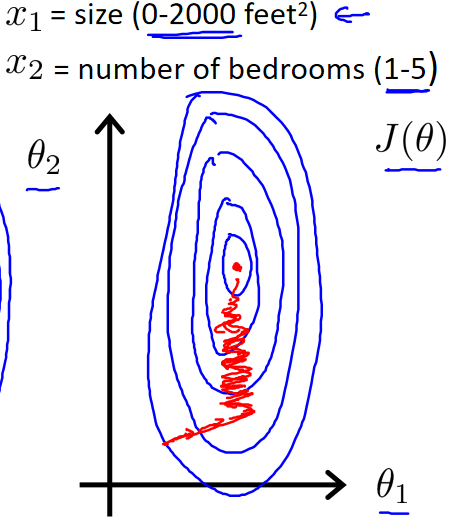
解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间。如图

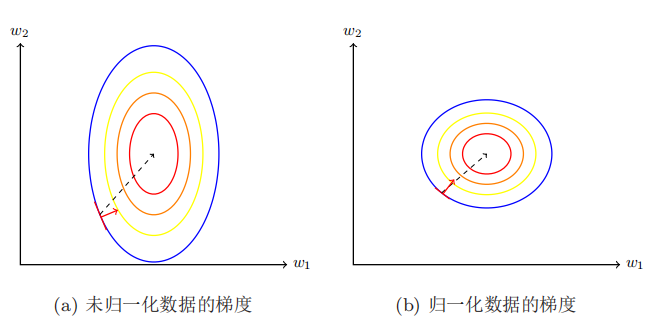
最简单的方法是令：$x_n^{\ast }=\frac{x_n-{\mu }_n}{s_n}$，即概率论中的标准化随机变量，${\mu }_n$是平均值，$s_n$是标准差或者为变量的范围。

学习率

如果$\alpha$太小或$\alpha$太大会出现什么情况：

1.如果$\alpha$太小了，即我的学习速率太小，这样就需要很多步才能到达最低点，收敛可能会很慢，因为它会一点点挪动，它会需要很多步才能到达全局最低点。

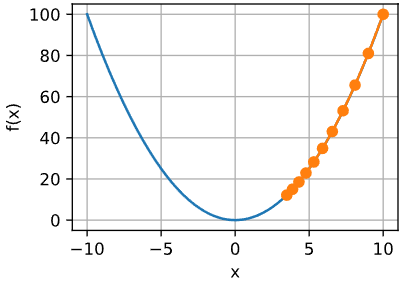
2.如果$\alpha$太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，所以，如果$\alpha$太大，它会导致无法收敛，甚至发散。

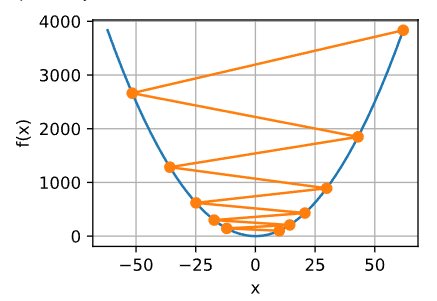
在梯度下降法中，当我们接近局部最低点时，梯度下降法会自动采取更小的幅度。这是因为局部最低时导数等于零，所以当我们接近局部最低点时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，直到$J$收敛于局部极小值，这就是梯度下降的做法。所以实际上没有必要再另外减小$\alpha$。这也解释了为什么即使学习速率$\alpha$保持不变时，梯度下降也可以收敛到局部最低点。

通常可以考虑尝试些学习率：
$\alpha =0.01,0.03,0.1,0.3,1,3,10$（大致按3倍增加）。,先选取一系列学习率，然后找到一个合适的范围，最后选取范围内较大的学习率。

特征和多项式回归

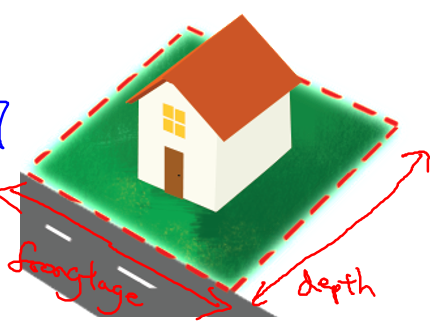
在房价预测问题中，我们可以选择两个特征：$x_1=frontage$(邻街宽度)，$x_2=depth$（纵向深度），由此得到假设函数$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$

但是我们选取特征:$x=frontage\ast depth=area$（面积），由此得到假设函数$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$（减少了一个特征）

有时候对同一个问题的不同特征选取可能会得到一个更好的模型。

线性回归并不适用于所有数据，有时需要曲线来适应数据。通常我们需要先观察数据然后再决定准备尝试怎样的模型。比如一个二次模型$h_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$或者三次模型： $h_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3$

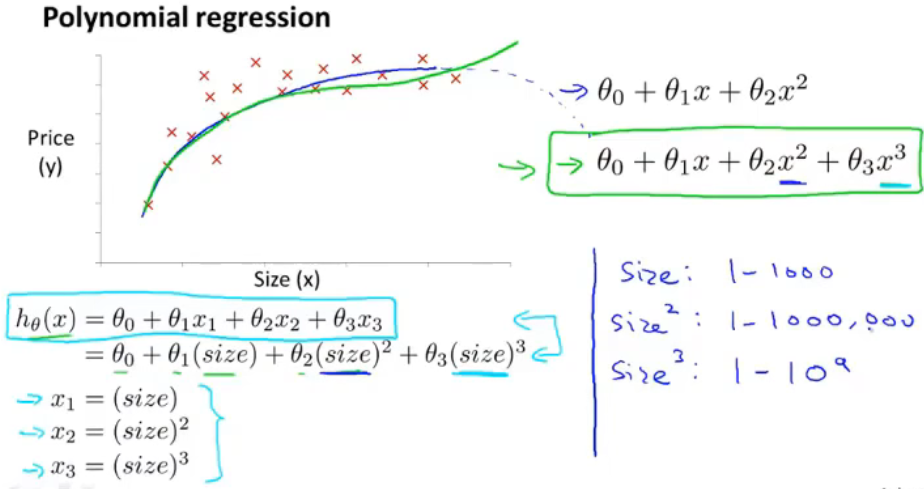
根据散点趋势我们可以令：$x_1=size,x_2=siz{e}^2$,从而得到假设：$h_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}_2$

由于二次函数不单调，不能很好的拟合数据，所以还可以令：$x_1=size,x_2=siz{e}^2,x_3=siz{e}^3$,从而得到假设：$h_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}_2+{\theta }_3{x}_3$

上述两种方法均将模型转化为线性回归模型。注意，如果我们采用多项式回归模型，在运行梯度下降算法前特征缩放非常有必要。

正规方程

到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，正规方程方法是更好的解决方案。

正规方程是通过求解方程$\frac{\partial J({\theta }_j)}{\partial {\theta }_j}=0$来找出使得代价函数最小的参数的。

推导过程：

梯度下降与正规方程的比较：

梯度下降	正规方程
需要选择学习率$\alpha$	不需要
需要多次迭代	一次运算得出
当特征数量n大时也能较好适用	需要计算$(X^{T}X{)}^{-1}$如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为$O(n^3)$，通常来说当n<10000 时还是可以接受的
广泛适用于各种类型的模型	只适用于线性模型，不适合逻辑回归模型等其他模型

逻辑回归（Logistic Regression）

分类问题

在分类问题中，要预测的变量 y是离散的值，我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法，这是目前最流行使用最广泛的一种学习算法。

我们从二元的分类问题开始讨论。

我们将因变量(dependent variable)可能属于的两个类分别称为负向类（negative class）和正向类（positive class），则因变量 y ∈ { 0 , 1 } y\in\{0,1\} y∈{0,1}，其中 0 表示负向类，1 表示正向类。

所以我们在接下来的要研究的算法就叫做逻辑回归算法，这个算法的性质是：它的输出值永远在0到1之间。

逻辑函数

我们希望找出一个满足预测值要在0和1之间的假设函数。回顾在一开始提到的肿瘤分类问题，我们可以用线性回归的方法求出适合数据的一条直线。假使我们又观测到一个非常大尺寸的恶性肿瘤，将其作为实例加入到我们的训练集中来，这将使得我们获得一条新的直线。

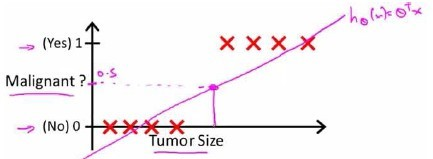
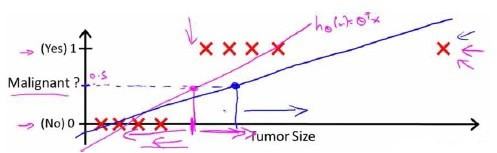
所以使用线性模型来解决这个分类问题并不合适，逻辑函数(logistic function) 正是这样一个常用的替代函数：
$$g(z)=\frac{1}{1+e^{-z}}$$
逻辑函数（logistic function)是一个常用的S形函数,所以又称为sigmoid函数。

将z作为线性回归模型带入sigmoid函数就能得到逻辑回归模型：
$$f_{\mathbf{w},b}({\mathbf{x}}^{(i)})=g(\mathbf{w}\cdot {\mathbf{x}}^{(i)}+b)=\frac{1}{1+e^{-\mathbf{w}\cdot {\mathbf{x}}^{(i)}+b}}$$

决策边界

决策边界(decision boundary)的概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。

我们将模型($f_{\mathbf{w}，b}(x)$)的输出解释为给定$x$并由$w$和$b$参数化的$y=1$的概率。因此，为了从逻辑回归模型中得到最终的预测($y=0$或$y=1$)，我们可以使用下面的预测规则：

如果$f_{\mathbf{w}，b}(x)>=0.5$，则预测$y=1$

如果$f_{\mathbf{w}，b}(x)<0.5$，则预测$y=0$

同时，$g(z)>=0.5$意味着$z>=0$，对于逻辑回归模型，$z=\mathbf{w}\cdot \mathbf{x}+b$，因此预测规则也可以是：

如果$\mathbf{w}\cdot \mathbf{x}+b>=0$，则模型预测$y=1$

如果$\mathbf{w}\cdot \mathbf{x}+b<0$，则模型预测$y=0$

假设我们的逻辑回归模型有如下形式$f(x)=g(-3+x_0+x_1)$，此模型有两个特征，它的数据分布：

我们令$x_0+x_1-3=0$，则这条直线将预测为1的区域和预测为 0的区域分隔开。

阴影区域表示$-3+x_0+x_1<0$。直线上方的区域$-3+x_0+x_1>0$。阴影区域(线下)的任何点被分类为$y=0$。直线上或以上的任何点都被分类为y=1。这条线被称为决策边界（Decision Boundary）。

逻辑回归的代价函数

假如我们继续使用线性回归中的均方误差函数来作为代价函数
$$J(w,b)=\frac{1}{2m}\sum _{i=0}^{m-1}(f_{w,b}(x^{(i)})-y^{(i)}{)}^2$$
where $f_{w,b}(x^{(i)})=g(w{x}^{(i)}+b)$

但这样我们得到的代价函数将是一个非凸函数,这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。

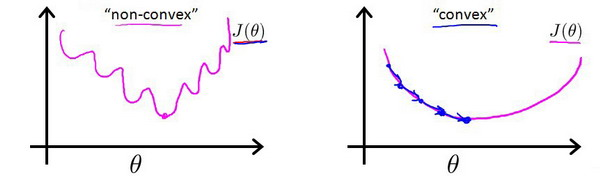
所以我们引入以下的函数来计算单个样本的损失（loss），此函数是通过极大似然法得出的
$$\begin{array}{c}loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})=\{\begin{array}{ll}-\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)& \text{if y(i)=1}\\ \log \left(1-f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)& \text{if y(i)=0}\end{array}\end{array}$$
**注:**在本课程中，使用了以下定义:**损失（loss）**是衡量单个示例与其目标值的差异。**代价（cost）**是对整个训练集损失的度量

这个函数包含了两个函数曲线来分别计算y=0或y=1的损失，事实上它工作的相当好。当真实值y=1时，预测值越接近1损失就越小，预测值越接近0损失就越大（趋向于无穷大）；当真实值y=0时，也亦然。

不过此损失函数也可以化简为只用一个函数式子的形式：

$$loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})=(-y^{(i)}\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)$$

上面已经定义了**代价（cost）**是对整个训练集损失的度量，所以逻辑回归的代价函数应写成：
$$J(\mathbf{w},b)=\frac{1}{m}\sum _{i=0}^{m-1}\left[loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})\right]$$
意为对所有样本的损失取平均值，得到代价（cost）

在得到这样一个代价函数以后，我们便可以用梯度下降算法来求得能使代价函数最小的参数了。

repeat until convergence:    {        w j = w j − α ∂ J ( w , b ) ∂ w j    for j := 0..n-1            b = b − α ∂ J ( w , b ) ∂ b } \begin{align*} &\text{repeat until convergence:} \; \lbrace \\ & \; \; \;w_j = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \; & \text{for j := 0..n-1} \\ & \; \; \; \; \;b = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \\ &\rbrace \end{align*} ​repeat until convergence:{wj​=wj​−α∂wj​∂J(w,b)​b=b−α∂b∂J(w,b)​}​for j := 0..n-1
求导后得到：
$$\begin{array}{rl}\frac{\partial J(\mathbf{w},b)}{\partial w_j}& =\frac{1}{m}\sum _{i=0}^{m-1}(f_{\mathbf{w},b}({\mathbf{x}}^{(i)})-y^{(i)})x_j^{(i)}\\ \frac{\partial J(\mathbf{w},b)}{\partial b}& =\frac{1}{m}\sum _{i=0}^{m-1}(f_{\mathbf{w},b}({\mathbf{x}}^{(i)})-y^{(i)})\end{array}$$
求导的推导过程：

我们可以发现虽然逻辑回归的$J(w,b)$与线性回归中的代价函数定义不同，但求导之后的形式是相同的。之前用于线性回归监控梯度下降收敛的方法，在此处同样适用。

pytorch

Dataset自定义数据集

使用pytorch我们可以自定义数据集。自定义数据集需要继承Dataset类，并重写__len__和__getitem__两个方法。

以下是一个自定义数据集的简单示例：

from torch.utils.data import Dataset
from PIL import Image
import os

class Mydata(Dataset):
    def __init__(self, root_dir:str, label_dir:str):
        self.root_dir = root_dir                # 数据所在的目录
        self.label_dir = label_dir              # 对应标签的目录
        self.path = os.path.join(self.root_dir, self.label_dir)
        self.img_path = os.listdir(self.path)   # 每一个图片数据的名称都在这个列表中

    def __getitem__(self, idx):
        img_name = self.img_path[idx]           # 通过下标获取图片数据的名称
        img_item_path = os.path.join(self.path, img_name)
        img = Image.open(img_item_path)
        label = self.label_dir
        return img, label                       # 返回这个图片的Image对象和标签

    def __len__(self):
        return len(self.img_path)               # 这个自定义数据集的数据数量

ants_dataset = Mydata("dataset/train", "ants") # 创建ants数据集
bees_dataset = Mydata("dataset/train", "bees") # 创建bees数据集
img, label = bees_dataset[1]    # 获取一个数据
img.show()                      # 展示图片

torch.utils.data.Dataset 是一个表示数据集的抽象类。任何自定义的数据集都需要继承这个类并覆写相关方法。

所谓数据集，其实就是一个负责处理索引(index)到样本(sample)映射的一个类(class)。

总结

本周补充了线性回归的一些细节，了解了常用于分类任务的逻辑回归模型，使用pytorch编写了一个dataset类的简单示例。下周将学习正则化相关的知识。