目录
一、前言
本文主要介绍了一个数据分析的简单项目,旨在为初入数据分析领域的学者提供学习分享。由于作者水平有限,文章内容可能存在不足之处,敬请指正批评。本文是一篇简单的“房屋价格预测分析”分析,结尾附带资源,内含数据、代码、论文写作等资源,希望对您有所帮助。最后,在开始前希望各位来个三连,您的支持是我继续奋斗的动力!
二、题目和数据
问题背景
“买房”已经成为当前社会的一个热词,很多人认为房子是必需品,买房是奋斗的动力之一,但是对于绝大多数人来说,拥有一套属于自己的房子并不是一件简单的事情。为保障以更实惠的价格购买到心仪的房子,了解房地产市场的变化是很有必要的,了解了市场的走向问题,也能更好的选择合适的时机购买房子,影响房屋价格的问题较多,所以在买房子之前一定要谨慎。若能对房价信息进行预测,使购买者得到更多的参考信息,买到性价比更高的房子,将会有非常重要的实际价值。
解决任务
1.请结合国家时事、地区经济和房屋户型等因素,来探讨影响房屋销售的因素。
2.在(1)的结果基础上,对房屋情况、房屋户型、房屋销售等资料进行分析,从中找寻影响房价的原因。
3.建立房价预测模型,并对所建立的模型进行必要的分析。 数据文件“house.xlsx”包含了成都、广州、上海等多个城市在 2016 年-2019年的房屋出售情况
数据展示



三、问题分析
问题一分析通过时事变化和资料翻阅,查找出影响房屋销售和价格的指标,并且对这些指标进行解读和探讨,大部分销售和房价的影响都是类似的,但存在部分影响指标要根据数据进行分析而得出的。
问题二分析基于问题一的探讨,对 house 文件数据进行预处理操作,将缺失值、异常值以及错位等数据进行恰当的处理。后对每个指标进行数量分布以及与房屋总价格关系的可视化,从而找出影响房屋销量和总价格的指标,对影响指标的值为标量进行哑变量操作,从而对影响指标特征进行归纳总结。
问题三分析基于问题二得出的影响房屋总价格的特征指标,选择了网格搜索随机森林(GSRE) 算法进行对房屋总价格进行预测。对模型进行参数优化选择,从而得出较好的预测效果。
问题假设假设一:数据真实有效可靠假设二:别墅的房屋没有设立电梯口,即为零梯
四、问题解决
4.1 问题一
请结合国家时事、地区经济和房屋户型等因素,来探讨影响房屋销售的因素
区域位置:区域的位置对房屋的销量和价格是重要影响因数之一。区域对房屋销量和价格影响主要体现在该区域的经济状况、交通便利、就业与工资等。如今社会的科技发展迅速,交通也越来越先进,而就业竞争也越来越大。很多人年轻人都想着在大城市发展和就业,因为相对来说大城市的就业选择的机会多,且医疗先进、交通便利等因素,但同样的大城市的房屋价格也相对来说比较高。
房屋朝向:房屋朝向的探讨有很多,在古代都是讲究着“坐北朝南”的房屋朝向,而现在有些建筑是根据客厅和主卧室的窗户来确定的房屋的朝向。购房者通常会考虑到房屋的通风和采光程度,部分人可能还会考虑到风水的问题。因此,房屋朝向对房屋的销量和价格有一定的影响。
所在楼层:楼层的高低各有各自的好坏。高楼层可以看到更好的视野,还可以体验到更好的采光和照射,但可能存在一定的安全系数风险等;而低楼层可以更好的方便进出家门,但可能会受到周围环境因素的影响以及防盗问题;中楼层夹杂在两者之间,相对来说比较多人选择的。
梯户比例:梯户比例是指单元楼电梯数和每层楼住户数的比例。梯户比例的值可以直接反映出该楼的人口密度人数和房屋户型结构。梯户比例越低,该层楼的人口数多,高峰期时刻人们等电梯的时间会变长;楼层的租户数多反映了单套面积就小;而梯户比例高,降低了社区的容积率,而且房价也相对昂贵;因此通常来说梯户比例较中等为好。
房屋户型:房屋户型主要包括四部分:卧室、客厅、厨房、卫生间。该指标相对来说也是影响房屋销量和价格的主要因素之一。房屋户型的设计、功能分区、空间位置以及空间利用等都是购房者的考虑因素。
房屋用途:房屋用途体现房屋价值的一个重要因素。房屋的用途有很多种,但通常以住宅、商住两用、别墅三者为主。相对来说,别墅的单位面积最贵,商住两用的单位面积最便宜,而人们大部分买房通常是以住宅为主,销量基本上以住宅为主。
装修情况:装修情况就对买的房屋的原始状态,决定了购房者买房后的工作安排。精装的装修情况相对简装和毛坯有很大的跨越,大部分人都喜欢此类装修;部分人都有自己的装修设计,可以选择简装,可以根据自己的想法去设计房屋。
配备电梯:现在很多房屋都配带有电梯的,在居住在高楼层的住户更加需要。电梯为住户提供高效便利的出行条件。配备电梯的房屋会更受购房者欢迎。
以上是对部分影响房屋销量和价格的指标进行解读,明白了各指标的原理和意思。其实影响房屋销量和价格的因素还有很多,但不同的区域数据,影响的因素指标也有不同。因此,要通过对数观察分析才能更好的确定影响因素指标。
4.2 问题二
对房屋情况、房屋户型、房屋销售等资料进行分析,从中找寻影响房价的原因
# 导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
import collections # 词频统计库
import wordcloud # 词云展示库
warnings.filterwarnings('ignore') # 设置忽略警告
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 设置公式符号
# 数据导入
df = pd.read_csv('房屋价格预测_new.csv',encoding='gbk',header=1)
# 数据选取和剔除
df = df.drop(columns=['编号', '房屋号码', '房本备件', '房屋图片', '房屋链接','房产权','挂牌时间','上次交易'])
df = df[df['房屋总价格'].notnull()].reset_index(drop=True) # 对总价格缺失的数据踢除
print(df.shape)
df.head(1)4.2.1 数据预处理
预处理一:错位值处理。针对文件里的数据,发现房屋用途为“别墅”的数据存在部分特征指标的数值发生了错位现象,通过移位方法将值平移到对应的特征指标下。在处理好错位后发现“别墅”对应的户型结构全部缺失,将其填充为“其他”。
预处理二:新增指标列。在处理错位数据时,发现“配备电梯”特征指标里有“集中供暖”、“自供暖”等指标值,这些不属于“配备电梯”特征指标的值,因此将其扩充一列特征指标为“房屋暖气”,并且将“集中供暖”、“自供暖”这些值移动到“房屋暖气”指标下。
预处理三:无用指标删。观察文件的指标后,发现“房屋号码”指标值发生了格式错误,无法纠正;“图片”和“链接”都是网页链接;“房产权”指标的值只有“70年”一个,这些指标无分析的意义与价值,因此将指标列进行了删除,还有“房本备件”、“编号”、“挂牌时间”和“上次交易”也是如此。
预处理四:缺失值处理。通过上述的操作后,发现有很多“暂无数据”的值,为了更好的统计缺失值,将表里的“暂无数据”统一替换为空值。本文是关于房屋价格预测的,所以首先将“房屋总价格”缺失值的数据行进行删除。
# 缺失值统计
for i in df.columns:
if len(df) !=len(df[df[i].notna()]):
num = len(df) - len(df[df[i].notna()])
print('%s 的缺失值数为: %s'%(i,num))
# 套内面积 和 房屋暖气 数据缺失严重,剔除指标
df = df.drop(columns=['套内面积','房屋暖气'])缺失值处理①:通过查找发现,“小区名字”和“所在区域”的缺失值都是来自同一行,通过该行的“房屋主题”可以快速的发现“小区名字”是“禄徽苑”;也通过该“小区名字”筛选知道该行的“所在区域”是“长丰北城”,将两个值填充上去。
# 查看“小区名字”的缺失值数据
df[df['小区名字'].isnull()]
# 查找小区名字有无“禄徽苑”,若有则填充
df[df['小区名字']=='禄徽苑'].head(2)
# 对小区名字和所在地区继续填充
df.iloc[23053,3:5] = ['禄徽苑','长丰北城']
df.iloc[23053:23054] 
缺失值处理②:通过观察发现“梯户比例”的缺失值几乎来自“房屋用途”为“别墅”里的数据,占有246个。因此从中找取另外一个非“别墅”的缺失值。发现该缺失值和处理“小区名字”的缺失值是同一行数据,因此很快发现相同小区的“梯户比例”值为“两梯四户”。处理好这个后,其余“梯户比例”的缺失值都来自“房屋用途”为“别墅”里的数据,本文假设“别墅”都没有设立电梯口,使得电梯数为零,而“别墅”的建筑类型不同,使得户数也不好确定,因此对别墅的“梯户比例”填充为“零梯X户”。
# 发现梯户比例的缺失值都是来自 房屋用途的别墅
# 提取非别墅的关于梯户比例的缺失值
df_tihu = df[df.房屋用途 != '别墅']
df_tihu[df_tihu.梯户比例.isnull()]
# 查找 小区名字 为“禄徽苑”的梯户比列值
df[df['小区名字']=='禄徽苑']['梯户比例']
# 对“普通住宅”中“梯户比例”为缺失的进行填充
df.loc[23053,'梯户比例'] = '两梯四户'
# 判断缺失值是否来自别墅
df.梯户比例.isnull().sum() == len(df[df.房屋用途=='别墅'])
# 缺失别墅填充“零梯X户”
df['梯户比例'] = df.梯户比例.fillna('零梯X户')
df.梯户比例.isnull().sum()缺失值处理③:剩下的缺失值难以找到规律以及独有的特征,但发现“户型结构”、“建筑类型”、“抵押信息”和“房屋年限”缺失的数据量不说很多,最多的为376条数据,为了让指标间的效果分析更好,将这些指标缺失的数据行进行删除。而“套内面积”和“房屋暖气”的缺失值皆超出原数据的一半,因此将这两列指标继续删;“配备电梯”的缺失值相对来说也比较多,也删除该指标。
# 将户型结构 、房屋年限、抵押信息和 建筑类型 缺失的数据删除
df = df[ df['户型结构'].notnull() ]
df = df[ df['抵押信息'].notnull() ]
df = df[ df['房屋年限'].notnull() ]
df = df[ df['建筑类型'].notnull() ].reset_index()
# 缺失值查看
for i in df.columns:
if len(df) !=len(df[df[i].notna()]):
num = len(df) - len(df[df[i].notna()])
print('%s 的缺失值数为: %s'%(i,num))
# 剩下2个指标的数据缺失不进行处理,查看数据的行列数以及指标
print(df.shape)
df.columns
预处理五:剔数值单位。观察到“房屋总价格”、“建筑面积”、“每平方米价格”这些指标值都带含有单位,为了更好分析出数值和特征指标、数值指标的关系,因此将他们单位给删除以及格式转换。
# 数值的单位替换
df['房屋总价格'] = df['房屋总价格'].apply(lambda x:float(x.replace('万','')))
df['每平方米价格'] = df['每平方米价格'].map(lambda x: float(x.replace('元/平米','')))
df['建筑面积'] = df['建筑面积'].apply(lambda x :float(x.replace('㎡','')))
df.head(1)
预处理六:别墅并建筑。“建筑类型”指标的“联排”、“独栋”、“叠拼”、“双拼”的值是别墅独有的特征指标值,为了更好的区分“别墅的建筑类型”和其他的“建筑类型”指标值,将别墅的“建筑类型”指标值和“别墅”进行合并连接在一起,如:“独栋别墅”。
# 提取别墅的数据
df_bieshu = df[df['房屋用途']=='别墅']
df_bieshu = df_bieshu[df_bieshu['建筑类型'].notnull()]
df_bieshu['建筑类型'] = df_bieshu['建筑类型'] + df_bieshu['房屋用途']
# 将df的部分行数据根据df_bieshu的索引进行替换
for i in df_bieshu.index:
df.loc[i] = df_bieshu.loc[i]
df.建筑类型.value_counts() 
预处理七:异常值处理。数值形式的指标只有“房屋总价格”、“每平方米价格”以及“建筑面积”,通过箱线图简单分析他们的异常值。可以发现这些指标的数值存在较多的异常,而“房屋总价格”在5000以上、“每平方米价格”在20万元/平米以上以及“建筑面积”在500平方米以上的值相对来说过于异常。为了更直观的分析出指标间与价格的关系,所以将那些过于异常的值进行删除。
data = df[['房屋总价格','每平方米价格','建筑面积']]
plt.figure(dpi=200,figsize=(13,5))
for i in range(3):
plt.subplot(1,3,i+1)
plt.boxplot(data.iloc[:,i])
plt.xlabel(data.columns[i])
plt.show()
df = df[df['房屋总价格']<5000]
df = df[df['每平方米价格']<200000]
df = df[df['建筑面积']<500].reset_index(drop=True)
df.head(1)
通过上面的简单预处理后,由删除“房屋总价格”缺失值后的24360行数据变化到了23229行数据,少了近1/24行的数据,相对总体言删除的数据不是很多,因此对后面的分析不会有太大影响。
4.2.2 所在区域可视化
词频统计
quyu_counts = collections.Counter(list(df['区域'])) # 对分词做词频统计
quyu_counts_top20 = quyu_counts.most_common(20) # 获取前20最高频的词
print(quyu_counts_top20)
# 区域 词频云
wc = wordcloud.WordCloud(font_path='C:/Windows/Fonts/simhei.ttf', # 设置字体格式
width=800, height=400, mode="RGBA",background_color=None,max_font_size=160) # 字体最大值
plt.figure(dpi=150)
wc.generate_from_frequencies(quyu_counts) # 从字典生成词云
plt.imshow(wc) # 显示词云
plt.axis('off') # 关闭坐标轴
plt.show() # 显示图像
平均总价格
数据中包含区域的有“小区名字”和“所在区域”,由于指标值数据过多,因此从“所在区域”里提取前两个字代表区域位置,处理后发现仍有149个区域数据。通过对区域数据值的房屋总价格和每平方米价格进行聚合得出平均值。
# 聚合计算平均总价值
quyu_tol_mean = df.groupby('区域')['房屋总价格'].agg('mean')
quyu_tol_mean = pd.DataFrame(quyu_tol_mean).sort_values(by='房屋总价格',ascending=False)
#颜色调用
color_name = 'Set3'
plt.get_cmap(color_name)
# color_choose=(9,0) #调用2个颜色
# color = plt.get_cmap(color_name)(color_choose) #绘图用的颜色
fig=plt.figure(figsize=(15,6))
ax1=fig.add_subplot(1,1,1)
# 平均总价格前20名的柱形图
x = quyu_tol_mean.index[0:20]
height = quyu_tol_mean['房屋总价格'].head(20)
ax1.bar(x=x,height=height,label='平均总价格')
plt.legend(loc='upper right')
for a,b in zip(x,height):
plt.text(a,b+0.02,'%.2f'%b ,ha='center',va='bottom' ,fontsize=10,color='black')
# 平均总价格前20名的词频折线图
ax2=ax1.twinx() # 共享x轴,添加一条y轴坐标
# 平均总价值前20区域的词频数
top_20_quyu_count =[]
for i in quyu_tol_mean.index[0:20]:
a = quyu_counts[i]
top_20_quyu_count.append(a)
ax2.plot(x,top_20_quyu_count,color='orange',linestyle='--',marker='o',linewidth=2,label='区域数量')
plt.legend(loc='upper center')
for a,b in zip(x,top_20_quyu_count):
plt.text(a,b+0.02,'%.0f'%b ,ha='center',va='bottom' ,fontsize=10,color='r')
plt.title('平均总价格前20的区域')
plt.show()
平均每平方米
# 聚合计算平均每平方米价格
quyu_per_mean = df.groupby('区域')['每平方米价格'].agg('mean')
quyu_per_mean = pd.DataFrame(quyu_per_mean).sort_values(by='每平方米价格',ascending=False)
fig=plt.figure(figsize=(15,6))
ax1=fig.add_subplot(1,1,1)
color_choose=(0)
color = plt.get_cmap(color_name)(color_choose)
ax1.spines['top'].set_color('none')
ax1.spines['right'].set_color('none')
x = quyu_per_mean.index[0:15]
height = quyu_per_mean['每平方米价格'].head(15)
ax1.bar(x=x,height=height,label='平均每平方米价格',color=color)
for a,b in zip(x,height):
plt.text(a,b+0.02,'%.2f'%b ,ha='center',va='bottom' ,fontsize=10,color='orange')
plt.legend(loc='upper right')
plt.title('平均每平方米价格前15的区域')
# 平均总价格前20名的词频折线图
ax2=ax1.twinx() # 共享x轴,添加一条y轴坐标
# 平均总价值前20区域的词频数
top_15_quyu_count =[]
for i in quyu_per_mean.index[0:15]:
a = quyu_counts[i]
top_15_quyu_count.append(a)
ax2.plot(x,top_15_quyu_count,color='orange',linestyle='--',marker='o',linewidth=2,label='区域数量')
plt.legend(loc='upper center')
for a,b in zip(x,top_15_quyu_count):
plt.text(a,b+0.02,'%.0f'%b ,ha='center',va='bottom' ,fontsize=10,color='r')
plt.show()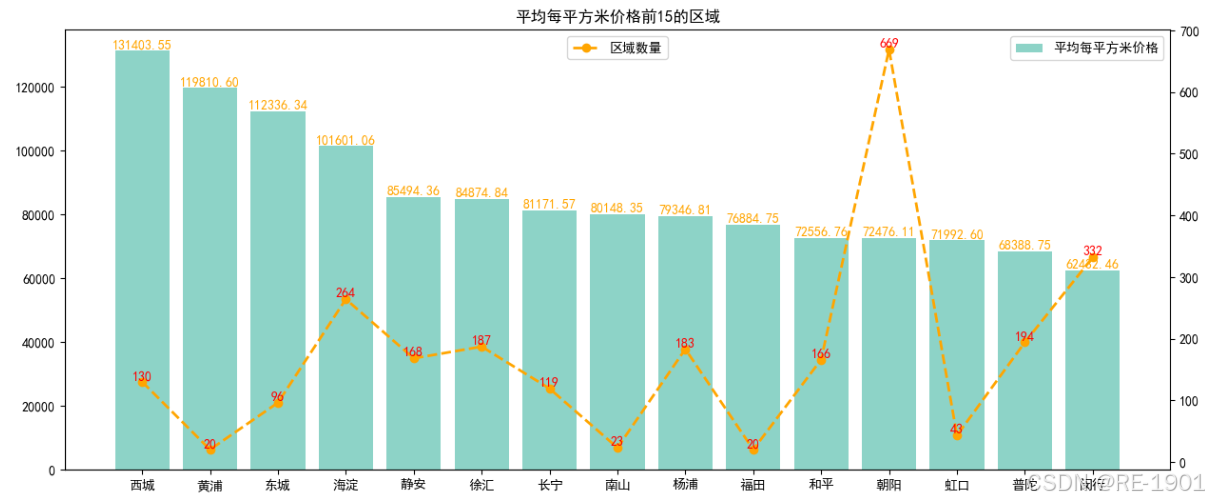
特征处理(为后续模型建立准备)
# 描述性统计
quyu_per_mean.describe().T
特征划分依据:平均每平方米
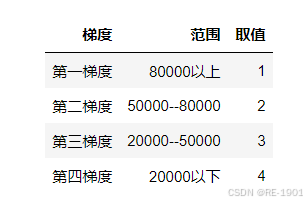
# 划分设置
quyu_tag = []
for i in quyu_per_mean['每平方米价格'].values:
if i >= 80000:
quyu_tag.append(1)
elif 50000<= i < 80000:
quyu_tag.append(2)
elif 20000<= i < 50000:
quyu_tag.append(3)
else:
quyu_tag.append(4)
quyu_per_mean['房屋区域'] = quyu_tag
quyu_per_mean = quyu_per_mean.drop(columns=['每平方米价格'])
quyu_dict = quyu_per_mean.to_dict()['房屋区域']
a = df_new.copy()
a['区域'] = df['区域']
a['房屋区域'] = 0
a = a.set_index(['区域'])
print(a.head(1))
# 区域填充
for i in a.index:
a.loc[i,'房屋区域'] = quyu_dict[i]
# 归到df_new表里
df_new['房屋区'] = a.index
df_new['房屋区域'] = a['房屋区域'].values
print(df_new.房屋区域.value_counts())
df_new.head()
最后划分结果依据:

4.2.3 建筑面积可视化
建筑面积(平方米) = 房屋总价格(元) / 每平方米价格(元/平方米)
直方分布图
# 显示数据集的分布
data=df[['每平方米价格','建筑面积','房屋总价格']]
plt.figure(figsize=(15,6))
plt.subplot(121)
sns.histplot(data,x='每平方米价格',bins=30, kde=True)
plt.subplot(122)
sns.histplot(data,x='建筑面积',bins=30, kde=True)
plt.show()
# 精化 --- 显示数据集的分布
data=df[['每平方米价格','建筑面积','房屋总价格']]
xxx1 = data.loc[data['每平方米价格'] <= 170000]
xxx2 = data.loc[data['建筑面积'] < 350]
fig = plt.figure(figsize=(15,6),dpi=200)
color_choose=(5)
color = plt.get_cmap(color_name)(color_choose)
ax1 = fig.add_subplot(1,2,1)
ax1.spines['top'].set_color('none')
ax1.spines['right'].set_color('none')
sns.histplot(xxx1,x='每平方米价格',bins=30, kde=True,color=color,label='每平方米价格')
plt.legend()
ax1 = fig.add_subplot(1,2,2)
color_choose=(9)
color = plt.get_cmap(color_name)(color_choose)
ax1.spines['top'].set_color('none')
ax1.spines['right'].set_color('none')
sns.histplot(xxx2,x='建筑面积',bins=30, kde=True,color=color,label='建筑面积')
plt.legend()
plt.show()
线性关系
# 建筑面积 和 房屋总价格 的关系
plt.rcParams['font.sans-serif']=['SimHei']
sns.lmplot(x='建筑面积',y='房屋总价格',data=data)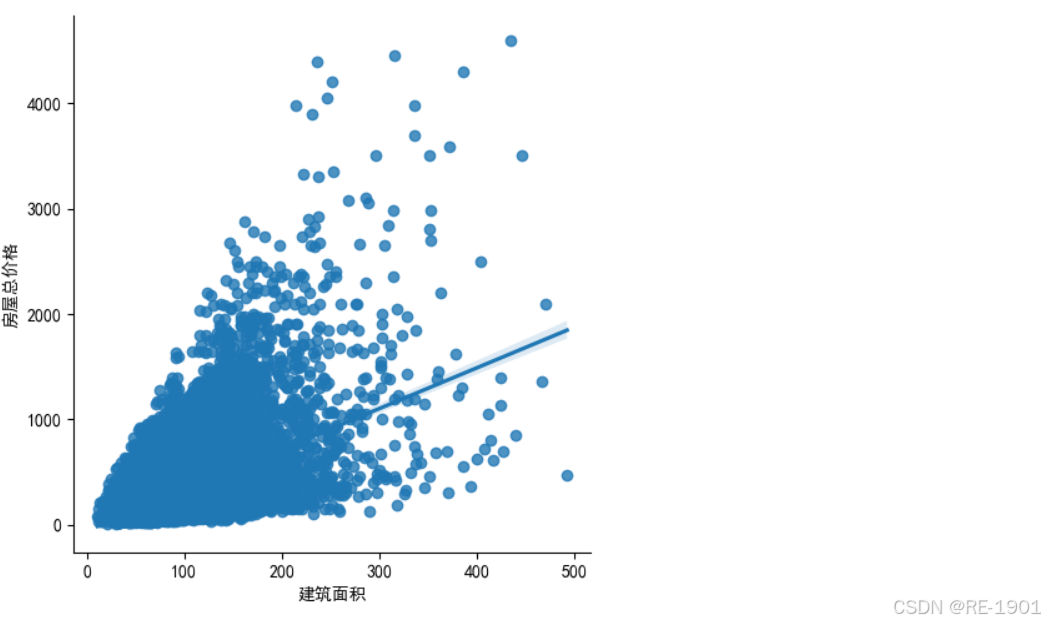
特征处理(为后续模型建立准备)
## df_new处理添加
df_new['每平方米价格']=df['每平方米价格']
df_new['建筑面积'] =df['建筑面积']
df_new.head(1)
4.2.4 房屋朝向可视化
# 查看朝向的个数和值
print(len(df.房屋朝向.unique()))
df.房屋朝向.unique() # 发现很多值是一样的,但顺序乱了
# 根据采光将各方向提取先后顺序提取到第一个位置
a = df.房屋朝向.apply(lambda x :x.split(' '))
for i in range(3):
print(list(a)[i])
# 提取第一位
df_dirction_1 = []
for i in list(a):
i.sort(key = lambda x : x.startswith('北'),reverse=True)
df_dirction_1.append(i)
df_dirction_2 = []
for i in df_dirction_1:
i.sort(key = lambda x : x.startswith('西北'),reverse=True)
df_dirction_2.append(i)
df_dirction_3 = []
for i in df_dirction_2:
i.sort(key = lambda x : x.startswith('东北'),reverse=True)
df_dirction_3.append(i)
df_dirction_4 = []
for i in df_dirction_3:
i.sort(key = lambda x : x.startswith('西'),reverse=True)
df_dirction_4.append(i)
df_dirction_5 = []
for i in df_dirction_4:
i.sort(key = lambda x : x.startswith('东'),reverse=True)
df_dirction_5.append(i)
df_dirction_6 = []
for i in df_dirction_5:
i.sort(key = lambda x : x.startswith('西南'),reverse=True)
df_dirction_6.append(i)
df_dirction_7 = []
for i in df_dirction_6:
i.sort(key = lambda x : x.startswith('东南'),reverse=True)
df_dirction_7.append(i)
df_dirction_8 = []
for i in df_dirction_7:
i.sort(key = lambda x : x.startswith('南'),reverse=True)
df_dirction_8.append(i)# 将得来的数据替换到df的表里
df['房屋朝向'] = df_dirction_8
print(df['房屋朝向'][0])
# 更改房屋朝向的格式
for i in range(len(df)):
df['房屋朝向'][i] = ' '.join(df['房屋朝向'][i])
# 重新查看朝向的个数和值
print(len(df.房屋朝向.unique()))
print(df['房屋朝向'][0])
df.房屋朝向.unique() # 发现还是有很多不同的值,将进行分类
# 重新设置索引
data = df[['房屋朝向']]
data = pd.DataFrame(data.value_counts(),columns=['count'])
data = data.reset_index(drop=False)
# 其余方向设置
data['房屋朝向']=data.房屋朝向.apply(lambda x:x if x in data['房屋朝向'].values[0:11] else '其他方向')
# 聚合
temp = data.groupby('房屋朝向')['count'].agg('sum').reset_index()
temp = temp.sort_values(by=['count'],ascending=False).reset_index(drop=True) # 降序排序
plt.figure(dpi=150)
#饼图参数设置
y=temp['count'].values
dev_position = [0.05 for _ in range(len(y))]
label=temp['房屋朝向'].values
#绘画饼图
plt.pie(y, # 画饼图的值,y值
explode=dev_position, # 饼图间隔,让他有脱离,不是紧密在一起,各类别的偏移半径
autopct='%0.2f%%', # 保留两位小数,百分比
labels=label , # 标签名称
startangle=170, # 逆时针角度设置
shadow=True,
pctdistance=0.8,
textprops={"fontsize":10} ) # 设置饼图中字体的大小
#优化设置
plt.title('房屋朝向数量的占比',color='orange')
#图形展示
plt.show()
特征处理(为后续模型建立准备)
# 指标太多,通过划分处理再分析与房屋总价格的关系
# 朝向分类:南、南+、偏南、非南
dirction_tag = []
for i in df_dirction_8:
if i[0] == '南' and len(i)==1:
dirction_tag.append('南')
elif i[0] == '南' and len(i)>1 :
dirction_tag.append('南+')
elif i[0] == '东南' or i[0] == '东' or i[0] == '西南':
dirction_tag.append('偏南 正东')
else:
dirction_tag.append('非南 非正东')
# 标签添加到df表里
df['dir_tag'] = dirction_tag
# 聚合均值
data = df[['房屋总价格','dir_tag']]
#data = data.groupby('dir_tag')['房屋总价格'].mean()
data
总价关系
sns.set_style('whitegrid')
plt.rcParams['font.sans-serif']=['SimHei']
data1=data[data['房屋总价格']<3000]
sns.boxplot(data=data1,x='dir_tag',y='房屋总价格')
plt.title('房屋朝向与总价关系')
plt.show()
## df_new处理添加
df_new['房屋朝向'] = df['dir_tag']
# 映射
xx = {'南':1,'南+':2,'偏南 正东':3,'非南 非正东':4}
df_new['房屋朝向']=df_new['房屋朝向'].map(xx)
df_new.head(1)
4.2.5 所在楼层、楼层数可视化


4.2.6 梯户比例可视化

4.2.7 房屋户型可视化


4.2.8 建筑、结构、装修

4.2.9 总结归纳
实际上分析其实不仅仅这几个,由于时间和精力的原因,还有几个角度没有编写出来,若感兴趣学习的朋友可以翻到最下面。

4.3 问题三
建立房价预测模型,并对所建立的模型进行必要的分析。 数据文件“house.xlsx”包含了成都、广州、上海等多个城市在 2016 年-2019年的房屋出售情况
4.3.1 随机森林(GSRF)
GSRF算法由随机森林和GridSearchCV组成。GridSearchCV是一种参数优化算法,通常用于微调机器学习模型中的超参数以优化其性能。它通过指定的参数网格进行迭代,并针对每个可能的参数组合对模型进行训练和评估,最终输出最佳参数集和相应的模型性能指标。
随机森林是一种机器学习算法,它是多个决策树的集合。随机森林的训练过程基于多棵决策树,算法在每棵决策树中随机选择一个特征子集进行训练。在预测过程中,随机森林通过平均或投票的方式将每个决策树的预测结果汇总,从而获得最终的预测结果。
与普通随机森林算法不同,GSRF算法可以使用最佳的超参数组合来训练和预测随机森林模型,显著提高了模型的性能。
df_new = df_new.drop(columns=['每平方米价格'])
df_new.head(1)
| 影响指标 | xi | 影响指标 | xi |
| 所在区域 | x1 | 房屋朝向 | x8 |
| 房屋用途 | x2 | 梯户比例 | x9 |
| 建筑面积 | x3 | 室 | x10 |
| 户型结构 | x4 | 厅 | x11 |
| 建筑类型 | x5 | 厨 | x12 |
| 建筑结构 | x6 | 卫 | x13 |
| 装修情况 | x7 | 房屋总价格 | y |
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import GridSearchCV
#from sklearn.linear_model import LinearRegression
#linear_regressor = LinearRegression() 线性回归
# 将数据集划分为训练集和测试集
X = df_new.iloc[:,2:]
y = df_new.iloc[:,0]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)4.3.2 调节参数
| 参数 | 参数解释 |
| max_depth | 树的最大深度,决定模型的复杂程度,取值越小越简单。 |
| n_estimators | 随机森林包含的决策树的个数,数值越高,模型更加准确。 |
| min_samples_split | 分裂内部节点需要的最少样例数。 |
# n_estimators
acc_ne_all=[]
train=[]
for i in range(1,100,1):
tree_ne = RandomForestRegressor(n_estimators=i) #确定深度时确定了最佳深度为16
tree_ne.fit(X_train, y_train)
c=tree_ne.fit(X_train, y_train)
y_pred_ne = tree_ne.predict(X_test)
acc_ne=r2_score(y_test, y_pred_ne)
acc_train =c.score(X_train,y_train)
acc_ne_all.append([i,acc_ne])
train.append(acc_train)
score_al = np.array(acc_ne_all)
max_acc_ne = np.where(score_al==np.max(score_al[:,1]))[0][0] # 找出最高得分对应的索引
print("最优参数以及最高得分:",score_al[max_acc_ne])
plt.figure(figsize=[16,5.5])
plt.plot(score_al[:,0],score_al[:,1],color="red",label="test")
plt.plot(range(1,100,1),train,color="blue",label="train")
plt.legend()
plt.show() 
# max_depth
acc_dep_all=[]
train=[]
for i in range(1,20,1):
tree_max_dep = RandomForestRegressor(n_estimators=int(score_al[max_acc_ne][0]) ,max_depth=i)
tree_max_dep.fit(X_train, y_train)
a=tree_max_dep.fit(X_train, y_train)
y_pred_dep = tree_max_dep.predict(X_test)
acc_dep=r2_score(y_test, y_pred_dep)
acc_train = a.score(X_train,y_train)
acc_dep_all.append([i,acc_dep])
train.append(acc_train)
score_all = np.array(acc_dep_all)
max_acc_dep = np.where(score_all==np.max(score_all[:,1]))[0][0]
print("最优参数以及最高得分:",score_all[max_acc_dep])
plt.figure(figsize=[16,5.5])
plt.plot(score_all[:,0],score_all[:,1],color="red",label="test")
plt.plot(range(1,20,1),train,color="blue",label="train")
plt.title('在不同 max_depth下观察模型的拟合状况')
plt.legend()
plt.show()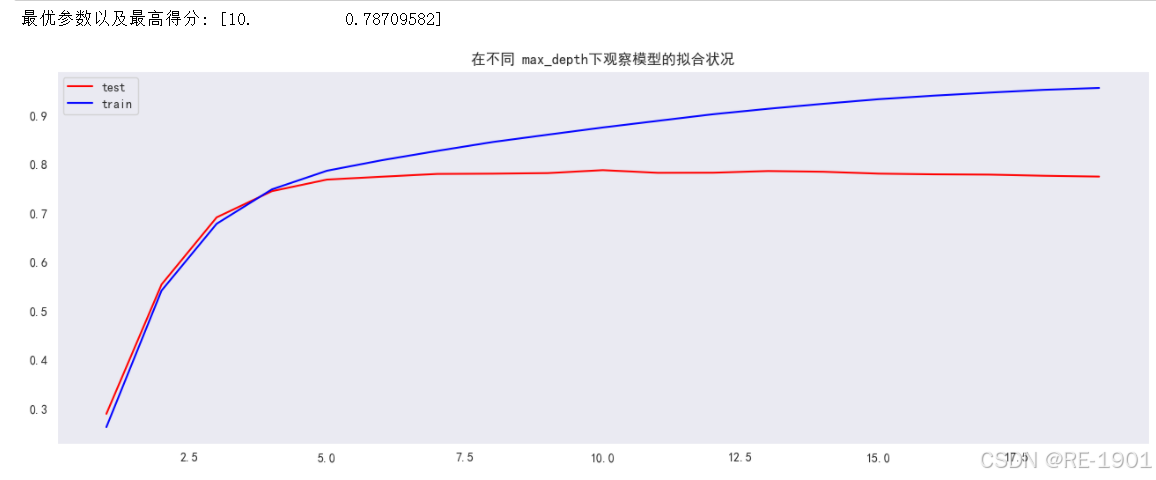
# min_samples_split
acc_mss_all=[]
train=[]
for i in range(2,20,1):
tree_mss = RandomForestRegressor(n_estimators=int(score_al[max_acc_ne][0])
,max_depth=int(score_all[max_acc_dep][0])
, min_samples_split=i) #确定深度时确定了最佳深度为16
tree_mss.fit(X_train, y_train)
b=tree_mss.fit(X_train, y_train)
y_pred_mss = tree_mss.predict(X_test)
acc_mss=r2_score(y_test, y_pred_mss)
acc_train = b.score(X_train,y_train)
acc_mss_all.append([i,acc_mss])
train.append(acc_train)
score_a = np.array(acc_mss_all)
max_acc_mss = np.where(score_a==np.max(score_a[:,1]))[0][0] # 找出最高得分对应的索引
print("最优参数以及最高得分:",score_a[max_acc_mss])
plt.figure(figsize=[16,5.5])
plt.plot(score_a[:,0],score_a[:,1],color="red",label="test")
plt.plot(range(2,20,1),train,color="blue",label="train")
plt.legend()
plt.show() 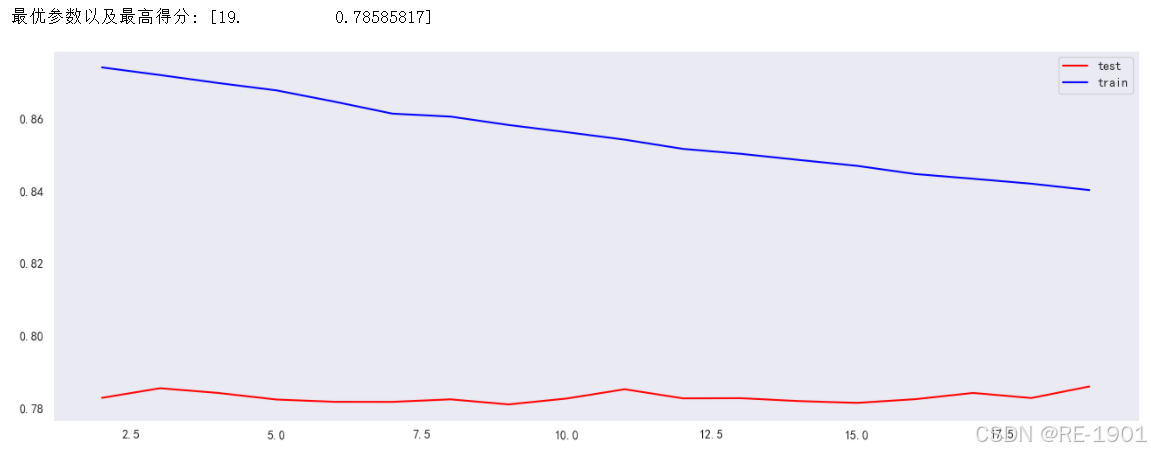
# 随机森林回归模型
rf_regressor = RandomForestRegressor()
#网格调优参数设置
parameter_tr= {'max_depth':np.arange(9,12),
'min_samples_split':np.arange(18,21),
'n_estimators':np.arange(82,85)}
#网格搜索调优参数
rf_regressor = GridSearchCV(rf_regressor,parameter_tr)
# 训练集模型训练
rf_regressor.fit(X_train, y_train)
# 测试集预测
y_pred = rf_regressor.predict(X_test)
#网格调优最优结果输出
print('最佳模型参数的评分:',rf_regressor.best_score_)
print('最佳结果的参数的组合:',rf_regressor.best_params_)
print("最佳参数的估计器:",rf_regressor.best_estimator_ )
通过三个参数的调优情况以及曲线分析,可以得到max_depth、min_samples_split、n_estimators三个参数值最好为10,19,83。但为了更好的探索最佳组合,通过网格搜索GridSearchCV寻找出最佳组合参数
4.3.3 模型结果
训练集
# 随机森林回归模型
rf_regressor = RandomForestRegressor(n_estimators=82,max_depth=11,min_samples_split=20, random_state=42)
# 训练集模型训练
rf_regressor.fit(X_train, y_train)
# 测试集预测
X_pred = rf_regressor.predict(X_train)
y_pred = rf_regressor.predict(X_test)
plt.figure(dpi=200,figsize=(20,8))
plt.title("训练集")
plt.plot(range(len(y_train)),y_train,label='真实值')
plt.plot(range(len(y_train)),X_pred,label='预测值')
plt.legend()
plt.show()

测试集
plt.figure(dpi=200,figsize=(20,8))
plt.title("测试集")
plt.plot(range(len(y_test)),y_test,label='真实值')
plt.plot(range(len(y_test)),y_pred,label='预测值')
plt.legend()
plt.show()

误差计算


可以知道大部分散点残差值都聚集在[-500,500]之间,也有少部分散点在绝对值为500开外的,说明了随机干扰项的值不大。从真实值和预测值可视化对比、MAE和RMSE以及决定系数的计算、散点残差图等多方面分析,总体归纳得出的GSRF模型的回归效果较好。因此得到回归方程:

五、资源获取
本文的题目、数据和代码全部在博客的资源了,若有需要可进行下载!
六、结束语
本文的分析至此基本完成,题目的难度相对简单。作为数据分析领域的初学者,我可能在内容上存在一些不足或错误之处。如果有任何资深人士发现这些问题,请不吝指出并给予指导,我会及时修改,以帮助大家采用更准确的方法进行学习和实践。
本文的源代码、论文、数据等等都已经绑定于博客的资源里!
若对这篇文章能对您的学习和工作有所帮助,请动动你的宝贵的小手指,点赞+收藏+关注!后续还会更新我自己写的笔记哦~



























 1286
1286

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








