大小端存储和char类型的范围解释

一* 大小端存储：

我们知道，数据在我们内存中存储，是先根据我们的变量类型(例如：int 整型)，开辟一个新的空间去存储数据(例如：int就是开辟一个4个字节的空间，32个bit位)。这个时候，计算机再根据要赋予变量的字面值转换成二进制的补码，再将补码存入内存中开辟的新空间。

问题来了：

在我们将二进制补码存入内存开辟的空间时，内存中开辟的空间有高低地址之分(例如：int对应四个字节，32个bit位的空间，一端地址是低地址，依次递增，到另一端就是高地址)，而我们的数据对于的二进制补码也会有字节的高权值位和低权值位。对于存储的方式就会有：

1.字节的低权值位存到内存空间的低地址位置，高权值位存到高地址的位置。

2.字节的低权值位存到内存空间的高地址位置，高权值位存到低地址的位置。

这两种存储方式分别叫小端存储和大端存储。

 

 注意：

我们计算机内内存空间实质上是存的二进制补码，但我们计算机显示，给我们看到的是十六进制的数字。

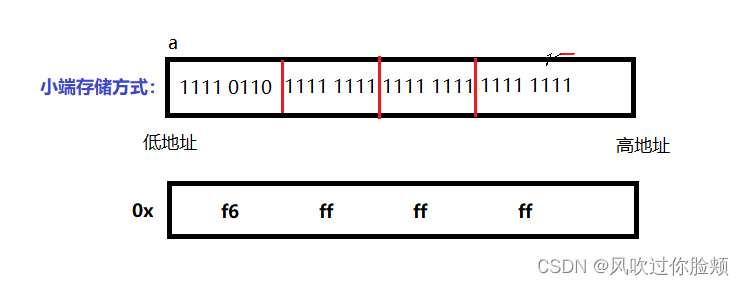
不难看出int a=-10这个例子，-10这个数在计算机内存中存储方式是小端存储，且存储的二进制补码，被以十六进制显示出来，为0xf6 ff ff ff。

二*char类型的范围解释：

首先我们知道char类型在内存中开辟一个字节，8个bit位的空间，若是unsigned char无符号char类型，它的范围是0~2^8-1(0~255)。若是signed char有符号char类型，第一位则考虑为符号(无非就是0和1)。后面7个bit位置.若是第一个位置是0，则它的范围是0~2^7-1(0~127)。若第一个位置是1，则它的范围是(-127~-0)。但是我们规定这个时候0还是(00000000)表示。而(10000000)则表示为-128。故signed char有符号char类型的范围是-2^7~2^7-1(-128~127)。

分析：

 

总结：

1.   一个有符号数的任意类型，在内存中开辟了n个bit位大小的空间。则它表示数据的范围：

-2^(n-1)~2^(n-1)-1

 1.   一个无符号数的任意类型，在内存中开辟了n个bit位大小的空间。则它表示数据的范围：

0~2^n-1