Kruskal求最小生成树的权值之和

【问题描述】
 已知含有n个顶点的带权连通无向图，采用邻接矩阵存储，邻接矩阵以三元组的形式给出，只给出不包括主对角线元素在内的下三角形部分的元素，且不包括不相邻的顶点对。求该连通图的最小生成树中各边的权值之和。
 注：三元组来表一条带权的边，如2 1 7表示顶点2到顶点1的边的权值为7.
【输入形式】
 第一行给出结点个数n和三元组的个数count，以下每行给出一个三元组，数之间用空格隔开。（注意这里顶点的序号是从1到n，而不是0到n-1，程序里要小心！）

【输出形式】
 最小生成树的权值

【样例输入】
 5 8
 2 1 7
 3 1 6
 3 2 8
 4 1 9
 4 2 4
 4 3 6
 5 2 4
 5 4 2

【样例输出】
 18

首先我们举个栗子

 并查集：就是一个用双亲表示法所表示的森林，我们可以用这个结构来查找一个顶点的双亲，进而找到根节点(Getroot),这样，我们就可以判断两个顶点是否同源（是否为同一个根节点），即在图中就是加上这条边后会不会形成环。

在该并查集里，数组的下标就是对应顶点的编号，而数组的值就是这个顶点所在的双亲

步骤：

1：对图的存储结构对权值按照进行从小到大的排序

 2:并查集进行初始化，数组的值就是其对应的下标

 3:选取存储结构里的第一项，查询对应顶点在并查集中是否同源，若不同则进行4，相同则进行5

4:若不同源，则把该边加入生成树，并计算和。修改前者的根在并查集中位置的值为后者的根。如下图：第一项(0,1)不同源，顶点0的根为0，顶点1的根为1，设a为并查集数组，把a[0] = 1，即把并查集中下标为0的位置中的值修改为1。这样，(0,1)这条路径就加入了最小生成树。

5:若同源，则跳过，继续遍历存储结构，如下图

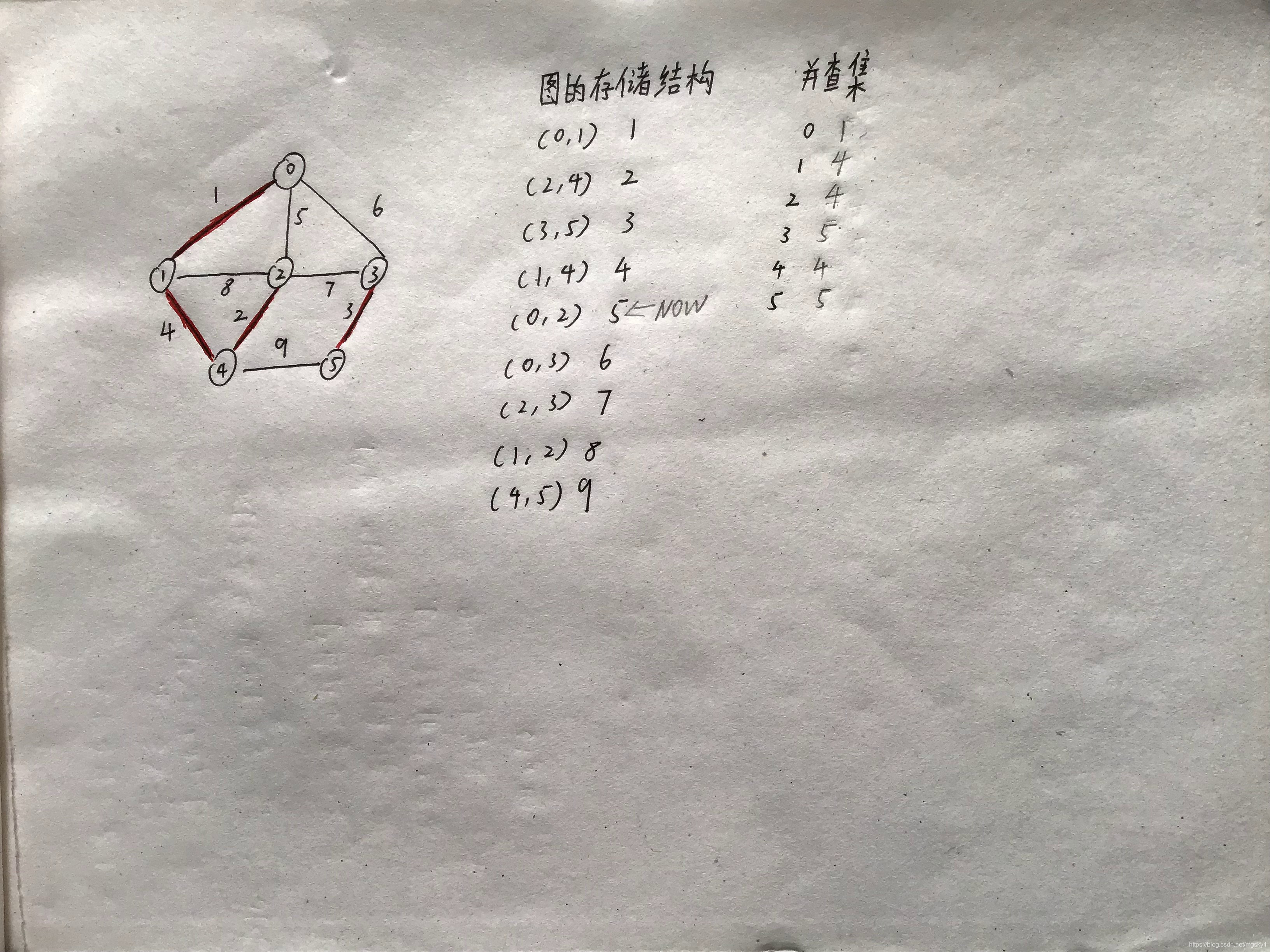
最后：Getroot（）函数，需要通过递归寻找根（而mark[x]=x则为其根），而不只是双亲

可判断0的根为4，而2的根为4，0和2同源，则跳过该项

#include<iostream>
#include<algorithm>
#include<math.h>
#include<cstdio>
int mark[100];      //全局变量 并查集
using namespace std;
typedef struct node
{
	int ii, jj;
	int cost;
}Node;
bool cmp(Node x,Node y)
{
	return x.cost< y.cost;
 }
int Comproot(int x) {
	if (x == mark[x])
		return x;
	else
		return Comproot(mark[x]);
}

int main()
	{
	int v, e;
	Node node[100];
	for (int i = 0; i < 100; i++)
	{
		mark[i] = i;               //初始化并查集 并用下标为其赋值
	}
	cin >> v >> e;
	                               //输入各条边的权值 数量由边数e决定
	for (int i = 0; i < e; i++)
	{
		cin >> node[i].ii >> node[i].jj >> node[i].cost;
	}
	sort(node, node + e, cmp);
	int sum = 0;
	for (int i = 0; i < e; i++)
	{
		int a = Comproot(node[i].ii);
		int b = Comproot(node[i].jj);
		if (a == b)
			continue;
		mark[a] = b;
		sum = sum + node[i].cost;
	}
	cout << sum;
	return 0;
	}