SVM（支持向量机）

最新推荐文章于 2025-10-09 01:34:11 发布

原创

最新推荐文章于 2025-10-09 01:34:11 发布 · 3.7k 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #svm #python

本文介绍了支持向量机（SVM）的基本原理，包括线性分类、非线性分类（核函数应用）以及松弛变量的概念。在非线性分类中，重点讨论了如何通过核函数简化高维空间的复杂运算。此外，还分享了基于sklearn库的SVM代码实现，探讨了不同核函数的选择对模型的影响。

一、SVM原理

1 SVM简介：

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。

简而言之，SVM的的学习算法就是求解凸二次规划的最优化算法。

2 线性分类

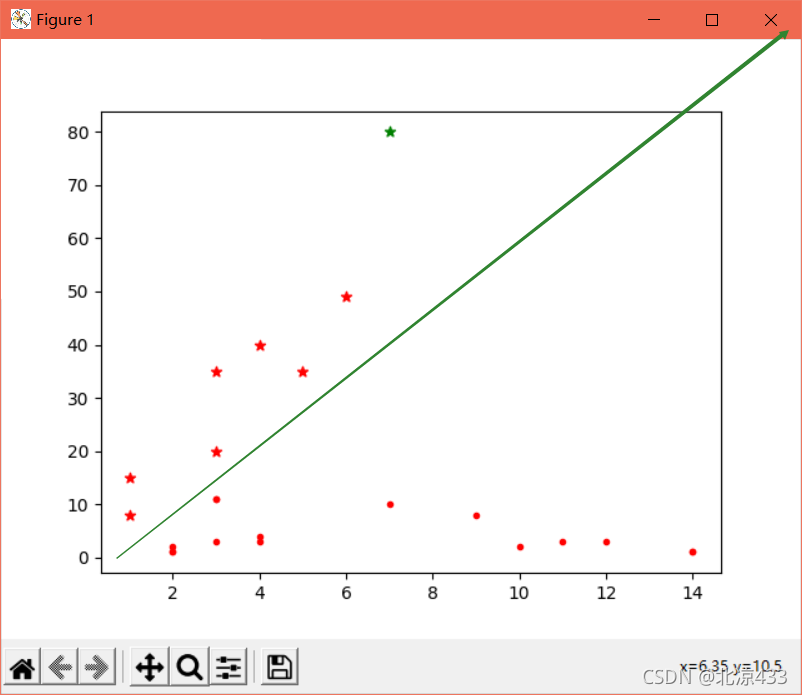
所谓线性分类，简而言之，一条线可以按照数据可分的原理将需要分类的数据划分开来。类似如下图所示：（也可详细解释为，从线性可分的数据讲起，如果需要分类的数据都是线性可分的，那么只需要一根直线f(x)=wx+b就可以分开了）

这种方法即被称为：线性分类器，一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面（hyper plane）。也就是说，数据不总是二维的，比如，三维的超平面是面。（在此只做了解）

引入知识要点：

1 几何分隔：对于给定的数据集来定义超平面关于样本点的几何间隔。具体详细讲解内容可参考此文章：支持向量机（SVM）——原理篇 - 知乎 (zhihu.com)

2 最大间隔分类器Maximum Margin Classifier：

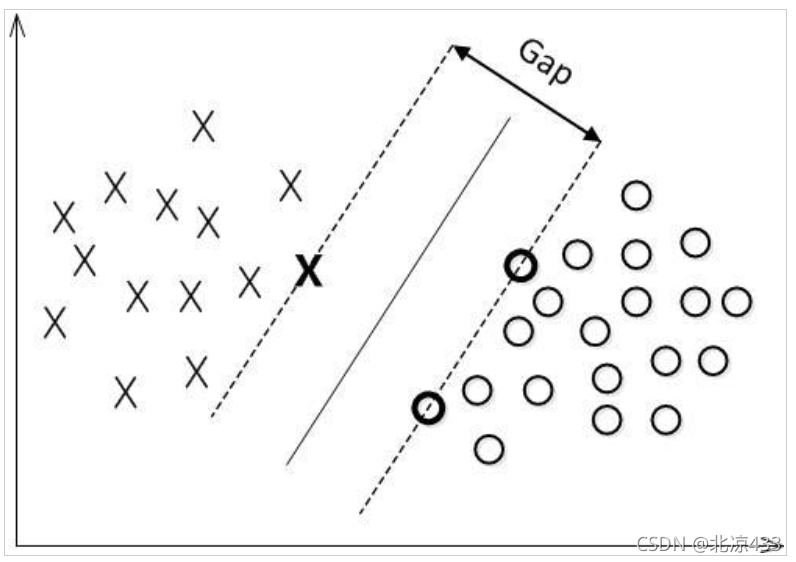
简称MMH，对一个数据点进行分类，当超平面离数据点的“间隔”越大，分类的确信度（confidence）也越大。所以，为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。

用以生成支持向量的点，如上图XO，被称为支持向量点，因此SVM有一个优点，就是即使有大量的数据，但是支持向量点是固定的，因此即使再次训练大量数据，这个超平面也可能不会变化。