支持向量机（Support Vector Mechine，SVC）

线性SVM

感知机模型

感知机模型是二分类线性判别模型，将所有误分样本的几何间隔作为损失函数，使用随机梯度下降法求解. 所有样本点正确分类时，模型学习完成，最终超平面与初始参数、梯度更新次序有关.

样本离超平面的距离，可近似模型对样本分类的可靠程度. 对于所有满足条件的超平面，距最近样本点距离最大的超平面为最优超平面. 基于此建立的线性可分模型为凸优化模型，解唯一.

点到超平面距离

对于超平面$\mathcal{H}:w^{\top }{x}^{\prime }+b=0$，则空间中任意点$x$到$\mathcal{H}$的距离为
$$\text{distance}(x,b,w)=\left|\frac{w^{\top }}{||w||}(x-x^{\prime })\right|=\frac{1}{||w||}|w^{\top }x+b|$$
证明： 若$x^{\prime }$是$\mathcal{H}$中的任意一点，$x$到$\mathcal{H}$的距离为$x-x^{\prime }$在$\mathcal{H}$法向量$w$上的投影，即
$$\text{distance}(x,b,w)=|{\text{porject}}_w(x-x^{\prime })|=\left|\frac{1}{||w||}w\cdot (x-x^{\prime })\right|$$

点到分类超平面的距离

若样本标签$y\in -1,+1$，样本$x$的预测标签为$\text{sign}(w^{\top }x+b)$，当超平面将$x$正确划分，则始终满足$y(w^{\top }x+b)\ge 0$，因此正确划分的$x$到$\mathcal{H}$的距离等价于
$$\text{distance}(x,b,w)=\frac{1}{||w||}y(w^{\top }x+b)$$

最大化最小几何间隔

缩放$w$可调整$x$到$\mathcal{H}$的函数间隔，为便于计算，令最小函数间隔为1，则最小函数间隔和几何间隔分别表示为
$$\gamma =y_i(w^T{x}_i+b)=1,\hat{\gamma }=\frac{\gamma }{||w||}=\frac{1}{||w||}$$
基于 最大化最小几何间隔 建立模型，优化问题为
$$\underset{w,b}{\max }\frac{1}{||w||}\text{s.t.}\min y_i(w^T{x}_i+b)=1$$
最小函数间隔为1，等价于所有样本的函数间隔大于等于1，优化问题等价于
$$\underset{w,b}{\max }\frac{1}{||w||}\text{s.t.}y(w^{T}x+b)\ge 1$$
等价形式为
$$\underset{w,b}{\max }\frac{1}{2}||w|{|}^2\text{s.t.}y(w^{T}x+b)\ge 1$$
上述问题为凸二次规划问题，有闭式最优解。

软间隔最大化线性SVM

线性不可分意味着存在一些样本点到超平面的函数间隔小于1，为解决这个问题，为每个样本点引入松弛变量${\xi }_i$，使得样本到超平面的函数间隔加上松弛变量后不小于1，并为每个松弛变量支付一个代价${\xi }_i$，则得软间隔最大化的线性SVM模型：
$$\begin{array}{rl}\underset{w,b,\xi }{\min }& \frac{1}{2}||w|{|}^2+C\sum _i{\xi }_i\\ \text{s.t.}& y_i(w^T{x}_i+b)\ge 1-{\xi }_i,{\xi }_i\ge 0\end{array}$$

优化目标是是几何间隔尽量大（$||w|{|}^2尽量小$），同时使误分类点数尽量少（${\xi }_i$尽可能为0）， 目标函数第一项为结构风险，第二项为经验风险。惩罚参数$C$代表模型误分类代价，$C$越大，模型倾向于将所有样本正确划分，模型倾向于过拟合，$C$越小，模型允许部分样本分类错误，模型倾向与欠拟合。

软间隔最大化与合页损失

合页损失（HInge loss）函数
$$\xi ={\ell }_{\text{hinge}}(z)=\max (0,1-z)⟹\xi \ge 1-z$$
即$z\ge 1$，$\xi =0$; $z<0$，$\xi =1-z$.

令函数间隔$z=y(w^{T}x+b)$，对于线性不可分问题，以合页函数作为损失函数并加入正则项，模型表示为（可用梯度下降法求解）
$$\underset{w,b}{\min }\sum _i{\ell }_{\text{hinge}}(y_i(w^T{x}_i+b))+\lambda ||w|{|}^2$$

令$\lambda =1/2C$，则上述优化问题等价于软间隔最大化SVM模型。LR使用交叉熵损失，关注全局实例，输出具有自然概率意义。

目标函数的对偶形式

原始约束极值问题的构造拉格朗日形式为
$$\underset{w,b,\xi }{\min }\underset{\alpha ,\mu }{\max }L(w,b,\xi ,\alpha ,\mu )=\underset{w,b,\xi }{\min }\underset{\alpha ,\mu }{\max }\left\{\frac{1}{2}||w|{|}^2+C\sum _i{\xi }_i-\sum _i{\alpha }_i[y_i(w^T{x}_i+b)-1+{\xi }_i]-\sum _i{\mu }_i{\xi }_i\right\}$$

原问题内部极大化是不等式约束的等价形式：

• 若存在不满足约束的$x_i$或${\xi }_i$，令${\alpha }_i\to +\infty$或${\mu }_i\to +\infty$，则$\underset{\alpha ,\mu }{\max }L=+\infty$;
• 若任意$x_i$满足约束，则$\underset{\alpha ,\mu }{\max }L=\frac{1}{2}||w|{|}^2+C{\sum }_i{\xi }_i$;

i. $\underset{w,b,\xi }{\min }L$，求$w,b,\xi$的偏导并令其为0，得
$$w=\sum _i{\alpha }_i{y}_i{x}_i,\sum _i{\alpha }_i{y}_i=0,C-{\alpha }_i-{\mu }_i=0$$

ii. $\underset{\alpha ,\mu }{\max }L$，带入上述结果，最优化问题转换为
$$\begin{array}{rl}& \underset{\alpha ,\mu }{\min }\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _i{\alpha }_i\\ & \text{s.t.}\sum _i{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,C-{\alpha }_i-{\mu }_i=0,{\mu }_i\ge 0\end{array}$$

消去${\mu }_i$得
$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _i{\alpha }_i\\ & \text{s.t.}\sum _i{\alpha }_i{y}_i=0,0\le {\alpha }_i\le C\end{array}$$

基于SMO算法求解约束方程解，$\alpha =({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n{)}^T$。

令$\mathcal{S}$表示$0<\alpha <C$的集合，则$y_i(w^T{x}_i+b)-1=0$，模型参数
$$w^{\ast }=\sum _{i\in \mathcal{S}}{\alpha }_i{y}_i{x}_i,b^{\ast }=\frac{1}{|\mathcal{S}|}\sum _{i\in \mathcal{S}}(y_i-w^T{x}_i)$$

实例点计算仅以內积形式出现，可自然引入核函数。

KKT条件和支持向量

KKT条件（最优解必要条件）
$$\{\begin{array}{l}{\nabla }_w=w-{\sum }_i{\alpha }_i{y}_i{x}_i=0\\ {\nabla }_b=-{\sum }_i{\alpha }_i{y}_i=0\\ {\nabla }_{\xi }=C-\alpha -\mu =0\\ {\alpha }_i(y_i(w^T{x}_i+b)-1+{\xi }_i)=0\\ \mu \cdot \xi =0\\ y_i(w^T{x}_i+b)-1+{\xi }_i\ge 0\\ \xi ,\alpha ,\mu \ge 0\end{array}$$
${\alpha }_i>0$对应的实例为支持向量，由KKT条件知支持向量满足
$$y_i(w^T{x}_i+b)-1+{\xi }_i=0$$

• ${\alpha }_i=0$，${\xi }_i=0$，样本位于边界之外（分类正确）；
• $0<{\alpha }_i<C$，${\xi }_i=0$，样本位于边界上（分类正确）；
• ${\alpha }_i=C$，$0<{\xi }_i<1$，样本位于超平面与边界之间（分类正确）；${\xi }_i=1$，样本位于超平面上；${\xi }_i>1$，样本位于边界之外（分类错误）；

非线性SVM和核函数

对于有限维数据，一定存在高维特征空间使样本线性可分. 对于非线性分类问题，首先需将原空间数据变换至新的特征空间（一般为高维），然后在新空间中使用线性分类方法学习分类模型.

SVM中引入核函数，得SVM的决策函数
$$f(x)=\text{sign}\left(\sum _i{\alpha }_i^{\ast }{y}_{i}K(x_i,x)+b^{\ast }\right)$$

核技巧

设$\varphi (x)$是一个从$\mathcal{X}$到$\mathcal{H}$的映射，对所有的$x,z\in \mathcal{X}$满足
$$K(x,z)=\varphi (x)\cdot \varphi (z)$$
定义核函数使得学习隐式地在特征空间中进行，不需要显式定义新的特征空间和映射函数，避免在新的高维空间中做內积运算.

对于映射$\varphi (x)=(x_1^2,\sqrt{2}{x}_1{x}_2,x_2^2{)}^T$，则
$$K(x,z)=(x\cdot z{)}^2=x_1^2{z}_1^2+2x_1{z}_1{x}_2{z}_2+x_2^2{z}_2^2=\varphi (x)\cdot \varphi (z)$$
在低维空间定义的运算等价于中完成高维空间的內积运算，二维空间$(x\cdot z{)}^2$等价于三维空间中$\varphi (x)\cdot \varphi (z)$.

正定核

核函数的条件：K对称，K对应的Gram矩阵半正定.

RBF核（Radial Basis Function Kernel，RBF）

$$K(x,z)=\exp (-\frac{1}{2}||x-z|{|}_2)$$

泰勒展开得
$$\begin{array}{rl}K(x,z)& =\exp (-\frac{1}{2}||x|{|}_2)\exp (-\frac{1}{2}||z|{|}_2)\exp (x\cdot z)=C_x{C}_z\exp (x\cdot z)\\ & =C_x{C}_z\left[1+x\cdot z+\frac{1}{2}(x\cdot z{)}^2+\cdots \right]\end{array}$$

RBF核等价于在无穷维空间中做內积，容易过拟合.

Sigmoid核

$$K(x,z)=\text{tanh}(x\cdot z)$$

决策函数
$$f(x)=\sum _i{\alpha }_i^{\ast }{y}_i\text{tanh}(x_i\cdot x)+b^{\ast }$$
等价于仅含有一层隐藏层的神经网络，隐藏层神经元个数等于支持向量数，激活函数为tanh函数.

序列最小最优化（Sequential Minimal Optimization，SMO）

引入核函数的线性SVM的对偶问题
$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _i\sum _j{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i\cdot x_j)-\sum _i{\alpha }_i\\ & \text{s.t.}\sum _i{\alpha }_i{y}_i=0,0\le {\alpha }_i\le C\end{array}$$
SMO算法启发式求解，若所有解满足KKT条件知，则所得解为最优解. SMO算法每次迭代只优化两个变量（等式约束限制，实际仅优化一个自由变量），固定其它变量，构建二次规划逐渐逼近最优解.

未剪辑解

假定优化变量${\alpha }_1,{\alpha }_2$，则最优化问题等价于
$$\begin{array}{rl}\underset{{\alpha }_1,{\alpha }_2}{\min }& W({\alpha }_1,{\alpha }_2)=\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2-({\alpha }_1+{\alpha }_2)\\ & +y_1{\alpha }_1\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i1}+y_2{\alpha }_2\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i2}\\ \text{s.t.}& {\alpha }_1{y}_1+{\alpha }_2{y}_2=-\sum _{i=3}^N{\alpha }_i{y}_i=\xi ,0\le {\alpha }_1,{\alpha }_2\le C\end{array}$$
${\alpha }_2$为自由变量，替换${\alpha }_1$，令$W$对${\alpha }_2$的偏导为0，得
$$(K_{11}+K_{22}-2K_{12}){\alpha }_2^{\ast }=y_2(y_2-y_1+\xi K_{12}-\xi K_{12}+\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i1}-\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i2})$$
令迭代前的预测偏差$E_j={\sum }_{i=1}^N{\alpha }_i{y}_i{K}_{ij}+b-y_j$，因此未剪短的最优解为
$${\alpha }_2^{\text{new,unc}}={\alpha }_2^{\text{old}}+\frac{y_2(E_1-E_2)}{K_{11}+K_{22}-2K_{12}}$$

剪辑解

由约束条件知，最优解位于平行于边长为C的正方形的对角线的线段上，如下所示

当$y_1=-y_2$，最优解${\alpha }_2$的界限
$$L=\max (0,{\alpha }_2^{\text{old}}-{\alpha }_1^{\text{old}}),H=\min (C,C+{\alpha }_2^{\text{old}}-{\alpha }_1^{\text{old}})$$
当$y_1=y_2$，最优解${\alpha }_2$的界限
$$L=\max (0,{\alpha }_1^{\text{old}}+{\alpha }_2^{\text{old}}-C),H=\min (C,{\alpha }_1^{\text{old}}+{\alpha }_1^{\text{old}})$$
因此剪短之后的最优解
$${\alpha }_2^{\text{new}}=\max (L,\min (H,{\alpha }_2^{\text{new,unc}})),{\alpha }_1^{\text{new}}={\alpha }_1^{\text{old}}+y_1{y}_2({\alpha }_2^{\text{old}}-{\alpha }_2^{\text{new}})$$

变量选择

初始$\alpha =0$，迭代时变量选择

• ${\alpha }_1$选择违反KKT条件最严重的变量，具体做法是$0<{\alpha }_i<C$的不满足KKT条件的实例，若均满足则在余下实例中查找；
• ${\alpha }_2$选择更新后变化较大的变量，${\alpha }_2$更新后变化程度正比于$|E_1-E_2|$，为简化计算，选择具有较大$|E_1-E_2|$的变量；

如何检验是否满足KKT条件（$ϵ$误差范围内检验）？
$$\alpha =\{\begin{array}{llc}0,& yg(x)\ge 1,& yE\ge -ϵ\\ (0,C),& yg(x)=1,& -ϵ\le yE\le ϵ\\ C,& yg(x)\le 1,& yE\le ϵ\end{array}$$
综上，不满足KKT条件等价于，当${\alpha }_i<C$，$y_i{E}_i<-ϵ$，或当${\alpha }_i>0$，$y_i{E}_i>ϵ$.

如何更新$b$值？
利用间隔边界上的点${\alpha }_1$或${\alpha }_2$更新$b$值，假定${\alpha }_1$位于间隔边界（任一间隔边界上的点均可），$0<{\alpha }_1<C$，则
$$\begin{array}{rl}{b}^{\text{new}}& =y_1-\sum _{i=3}^N{\alpha }_i{y}_i{K}_{i1}-{\alpha }_1^{\text{new}}{y}_1{K}_{11}-{\alpha }_2^{\text{new}}{y}_2{K}_{12}\\ & =-E_1-y_1{K}_{11}({\alpha }_1^{\text{new}}-{\alpha }_1^{\text{old}})-y_2{K}_{12}({\alpha }_2^{\text{new}}-{\alpha }_2^{\text{old}})+b^{\text{old}}\end{array}$$
若${\alpha }_1$和${\alpha }_2$均位于间隔边界，则分别计算取均值作为新的$b$值. 可见，保存并更新预测误差能加速计算.

如何更新误差$E$值？
若每次更新${\alpha }_1$和${\alpha }_2$两个变量，比较更新前后误差值
$$E_j=\{\begin{array}{ll}\sum _{i=3}^N{\alpha }_i{y}_i{K}_{ij}+{\alpha }_1^{\text{old}}{y}_1{K}_{j1}+{\alpha }_1^{\text{old}}{y}_1{K}_{j1}+b^{\text{old}},& 更新前\\ \sum _{i=3}^N{\alpha }_i{y}_i{K}_{ij}+{\alpha }_1^{\text{new}}{y}_1{K}_{j1}+{\alpha }_1^{\text{new}}{y}_1{K}_{j1}+b^{\text{new}},& 更新后\end{array}$$
因此，误差的更新公式为
$$E_j^{\text{new}}=E_j^{\text{old}}+({\alpha }_1^{\text{new}}-{\alpha }_1^{\text{old}})y_1{K}_{j1}+({\alpha }_2^{\text{new}}-{\alpha }_2^{\text{old}})y_2{K}_{j2}+b^{\text{new}}-b^{\text{old}}$$

Python实现SVC

# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
from numpy import *


class Kernel:

    @staticmethod
    def linear():
        return lambda x, y: float(inner(x, y))

    @staticmethod
    def gaussian(sigma):
        return lambda x, y: exp(
            float(linalg.norm(x - y)) ** 2 / (-2 * sigma ** 2))

    @staticmethod
    def _polykernel(dimension, offset):
        return lambda x, y: (offset + float(inner(x, y))) ** dimension

    @classmethod
    def inhomogenous_polynomial(cls, dimension):
        return cls._polykernel(dimension=dimension, offset=1.0)


class SVC:

    def __init__(self, kernel, C=0.5, max_iter=1000, eps=1e-3):
        """
        构造函数
        :param kernel: 核函数指针
        :param C: 惩罚参数
        :param max_iter: 无任何变量改变时的最大迭代次数
        :param eps: KKT条件检验范围（容错率）
        """
        self.C = C
        self.kernel = kernel
        self.max_iter = max_iter
        self.eps = eps

    def fit(self, X, y):
        """
        训练模型
        :param X: 输入特征集, 样本数*特征数
        :param y: 输入标签集, 1*样本数, 类别为+1或-1
        :return: self
        """
        self._X = mat(X, dtype=float64)
        self._Y = mat(y, int8).T
        n_samples, n_features = X.shape

        # 初始化alpha、gram矩阵、误差矩阵
        self._K = self.__gram_matrix(self._X)

        self._E = mat(-self._Y, dtype=float64)
        self._alphas = mat(zeros((n_samples, 1)))
        self.b = 0

        # 是否遍历全部变量
        entire = True

        # 内循环有效更改变量次数
        pair_changed = 0

        for _ in range(self.max_iter):
            print('iter:', _)
            # 若已遍历全部变量, 变量未有效更新, 则终止循环
            if not entire and pair_changed == 0:
                break
            pair_changed = 0
            if entire:
                for i in range(n_samples):
                    pair_changed += self.__inner_loop(i)
            else:
                for i in where((self._alphas > 0) & (self._alphas < self.C))[0]:
                    pair_changed += self.__inner_loop(i)

            # 若已遍历全部变量, 则下次一定遍历边界变量;
            # 若已遍历边界变量, 变量得到有效更新，则下次仍遍历边界变量;
            entire = False if entire else pair_changed == 0

        # 计算模型
        sv = where(self._alphas > 0)[0]
        self.sv_X = self._X[sv]
        self.sv_Y = self._Y[sv]
        self.sv_alphas = self._alphas[sv]
        self.w = (multiply(self.sv_alphas, self.sv_Y).T * self.sv_X).T
        return self

    def __inner_loop(self, i):
        """内循环"""
        # 临时变量, 用于减少访问, 加速计算
        alphas, b, C, E, K = self._alphas, self.b, self.C, self._E, self._K

        alphaIold, Yi, Ei = alphas[i, 0], self._Y[i, 0], E[i, 0]
        # 满足KKT条件, 则跳出本次循环
        if not (
                alphaIold < C and Yi * Ei < -self.eps or alphaIold > 0 and Yi
                * Ei > self.eps):
            return 0

        # 选择第二个变量
        j = self.__select_j(i)
        alphaJold, Yj, Ej = alphas[j, 0], self._Y[j, 0], E[j, 0]

        # 计算剪辑边界
        if Yi == Yj:
            L = max(0, alphaJold + alphaIold - C)
            H = min(C, alphaJold + alphaIold)
        else:
            L = max(0, alphaJold - alphaIold)
            H = min(C, C + alphaJold - alphaIold)
        if L == H:
            return 0
        eta = K[i, i] + K[j, j] - 2.0 * K[i, j]
        if eta == 0:
            return 0

        # 更新第二个变量
        unc = alphaJold + Yj * (Ei - Ej) / eta
        alphas[j, 0] = H if unc > H else L if unc < L else unc
        deltaJ = Yj * (alphas[j, 0] - alphaJold)

        # 更新第一个变量
        alphas[i, 0] -= Yi * deltaJ

        # 更新b值
        deltaI = Yi * (alphas[i, 0] - alphaIold)
        b1 = b - Ei - deltaI * K[i, i] - deltaJ * K[i, j]
        b2 = b - Ej - deltaI * K[i, j] - deltaJ * K[j, j]
        if 0 < alphas[i, 0] < C:
            self.b = b1
        elif 0 < alphas[j, 0] < C:
            self.b = b2
        else:
            self.b = 0.5 * (b1 + b2)

        # 更新误差矩阵
        E += ([deltaI, deltaJ] * K[[i, j]]).T + (self.b - b)

        return 1 if abs(deltaJ) > 0.00001 else 0

    def score(self, X, y):
        """
        计算模型预测正确率
        :param X: 输入特征集, m*n
        :param y: 输入标签集, 1*m
        :return: 0~1
        """
        y_ptd = self.predict(X)
        error_nums = len(where(y_ptd != mat(y).T)[0])
        return 1 - error_nums / len(X)

    def predict(self, X):
        """
        预测类别
        :param X: 输入特征集, m*n
        :return: 各样本类别, m*1
        """
        X = mat(X)
        kernel = self.kernel
        sv_X = self.sv_X
        K = mat([[kernel(x, xi) for xi in sv_X] for x in X])
        y = mat([1] * len(X)).T
        y[K * multiply(self.sv_alphas, self.sv_Y) + self.b < 0] = -1
        return y

    def __gram_matrix(self, X):
        """
        计算gram矩阵, 用于加速计算
        :param X: 输入特征集
        :return: gram矩阵
        """
        n_samples, n_features = X.shape
        K = mat(zeros((n_samples, n_samples)))
        # 利用核函数计算内积
        for i, x_i in enumerate(X):
            for j, x_j in enumerate(X[:i + 1]):
                K[i, j] = K[j, i] = self.kernel(x_i, x_j)
        return K

    def __select_j(self, i):
        """
        通过最大化步长的方式来获取第二个alpha值的索引.
        :param i: 第一个变量编号
        :return: 第二个变量编号
        """
        j, E = i, self._E

        # 查找最小误差的变量编号
        if E[i] > 0:
            min_error = inf
            for k in where((self._alphas > 0) & (self._alphas < self.C))[0]:
                if k != i and E[k] < min_error:
                    j, min_error = k, E[k]
        # 查找最大误差的变量编号
        else:
            max_error = -inf
            for k in where((self._alphas > 0) & (self._alphas < self.C))[0]:
                if k != i and E[k] > max_error:
                    j, max_error = k, E[k]
        while j == i:
            j = random.randint(0, self._X.shape[0])
        return j


if __name__ == '__main__':

    def load_data(filename):
        """读取数据"""
        X, y = [], []
        with open(filename) as f:
            for line in f.read().strip().split('\n'):
                line_array = line.split('\t')
                X.append(line_array[:-1])
                y.append(line_array[-1])
        return array(X, float64), array(y, float64)


    def plot_2Dsvm(X, y, w, b, alphas):
        """显示二维SVM"""
        X, y = array(X), array(y)

        fig = plt.figure()
        ax = fig.add_subplot(111)

        # 绘制样本散点图
        colors = array(['g'] * X.shape[0])
        colors[y > 0] = 'b'
        ax.scatter(X[:, 0], X[:, 1], s=30, c=colors, alpha=0.5)

        # w1x+w2y+b=0, 取两点绘制超平面及间隔
        x_min = X[where(X[:, 0] == X[:, 0].min())[0], 0]
        x_max = X[where(X[:, 0] == X[:, 0].max())[0], 0]
        x = array([x_min, x_max])
        y = (- b - w[0, 0] * x) / w[1, 0]
        y1 = (- b - linalg.norm(w, 2) - w[0, 0] * x) / w[1, 0]
        y2 = (- b + linalg.norm(w, 2) - w[0, 0] * x) / w[1, 0]
        ax.plot(x, y, 'r')
        ax.plot(x, y1, 'r--', alpha=0.2)
        ax.plot(x, y2, 'r--', alpha=0.2)

        for k in where(alphas > 0)[0]:
            plt.scatter(X[k, 0], X[k, 1], color='', edgecolors='r', marker='o',
                        s=150)
        plt.show()


    X, y = load_data(r"D:\testSet.txt")
    svc = SVC(kernel=Kernel.linear(), C=2)
    # svc = SVC(kernel=Kernel.gaussian(0.6), C=20)
    svc.fit(X, y)
    print(svc.score(X, y))

    plot_2Dsvm(X, y, svc.w, svc.b, svc._alphas)

数据集百度云链接：https://pan.baidu.com/s/1BmphBTCQLUV-djorG8JdwQ 提取码：krs9

线性可分SVM	线性不可分SVM
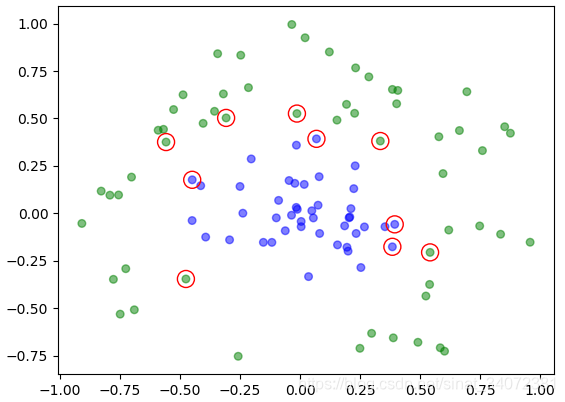非线性SVM-1	非线性SVM-2