多项式拟合的数学原理及实现

最小二乘曲线的拟合就是对于给定的数据（X,Y),(X=xi,Y=yi,i=1,2,3,......,N)，选取线性无关的函数族,及权函数v(x)(v(xi)表示数据(xi,yj)的权重），要求在函数类中寻找一个函数

使得达到最小

令

根据多元极值条件

其中，j=0,1,2,......,m。引入内积

方程可以表示为：

则：

取，即取{1,x,......,xm}为基函数的多项式拟合时，对应以上正规方程组就变为：

逐个计算出方程组系数矩阵与右端项的各个元素值，即可求的方程组的解，最后得到拟合多项式：

并用来判断拟合效果

下面将使用python代码进行实践

用这个函数，取x从0到10，区间分为100段，生成对应x和y

生成好之后，就可以用PolynomialFeatures函数生成x的多项式，然后进行拟合

import math
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
import statsmodels.api as sm
import matplotlib.pyplot as plt

# 定义x的取值范围
x_values = [i / 10 for i in range(1, 101)]  # 从0.1到1.0，步长为0.1

# 计算每个x值对应的y值
y_values = [math.exp(x) for x in x_values]

# 打印结果
print(x_values)
print(y_values)
# 多项式拟合
for degree in range(1, 6):
    print(degree)
    x = np.array(x_values).reshape(-1, 1)
    # 多项式特征转换
    poly = PolynomialFeatures(degree=degree)
    x_poly = poly.fit_transform(x)
    y=np.array(y_values).reshape(-1,1)
    # 线性回归模型拟合
    model = sm.OLS(y,x_poly).fit()
    print(model.summary())
    # 使用 scatter 方法绘制散点图
    plt.scatter(x, y)
    # 绘制数据点的拟合线
    y_pred=model.predict(x_poly)
    plt.plot(x, y_pred, color='green', linestyle='--', label='OLS Fit Line')
    # 可以添加标题和标签
    plt.title('Simple Scatter Plot')
    plt.xlabel('X Axis Label')
    plt.ylabel('Y Axis Label')

    # 显示图形
    plt.show()

效果如下：

在多项式最高次为1时：

        拟合优度为0.48，拟合线和散点关系如下图：

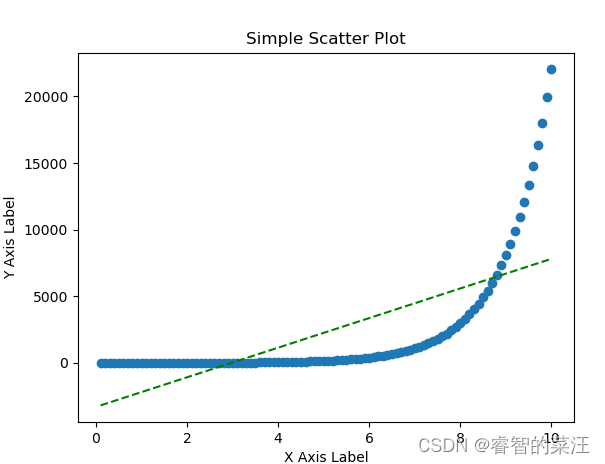
随着次数增高，拟合优度越来越好，拟合的曲线越来越接近

        在最高项次数为5次时，拟合优度非常接近1，图像如下图：

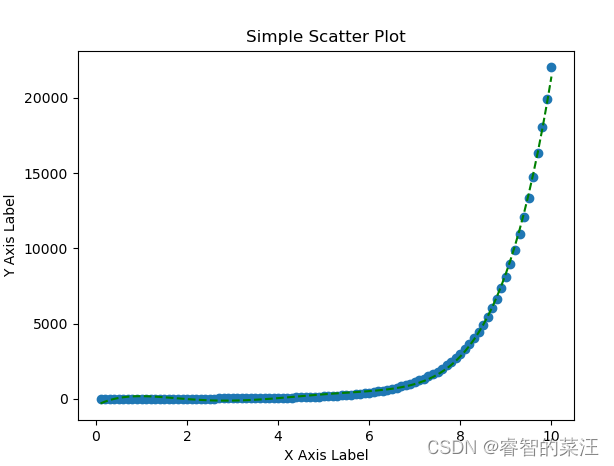
        可以看到拟合的比较好，在这一区间也可以明显看到拟合优度逐步上升。