矩阵范数定义及常用范数

一.矩阵范数的定义

        假设矩阵 ，定义一个实值函数，当实值函数满足非负性：

当时，；

当时，；

齐次性：

                                                                                       

三角不等式：

                                ​​​​​​​        ​​​​​​​        ​​​​​                           ​​​​​ 

则可以称实值函数为的广义矩阵范数。

        对于上的同类广义矩阵范数，若满足相容性：

                                                    ​​​​​​​        ​​​​​​​        ​​​​​​​              

则可以称为矩阵的矩阵范数。

二.常用矩阵范数

1.矩阵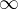-范数（行和范数）

        矩阵的行和范数（也称为最大绝对行和范数或称为∞-范数）是一种特定的矩阵范数，它通过取矩阵所有行的元素绝对值之和的最大值来定义。对于一个给定的 m×n矩阵 A，其行和范数定义为：

2.矩阵1-范数（列和范数）

        矩阵的列和范数是矩阵范数的一种，它定义为矩阵每一列元素绝对值之和的最大值。对于一个 m×n 的矩阵 A，其列和范数定义为：

3.矩阵2-范数（谱范数）

        矩阵的2-范数，也称为谱范数。对于一个给定的矩阵 A，其2-范数定义为矩阵的最大奇异值。奇异值是矩阵 的特征值的平方根，其中是 A 的共轭转置矩阵。其谱范数的的定义为：

4.矩阵F-范数（Frobenius范数）

         矩阵的F-范数（Frobenius范数）是一种特殊的矩阵范数，它在数学上的地位类似于向量范数中的欧几里得范数（L2范数）。F范数的定义是矩阵中所有元素的平方和的平方根。具体来说，对于一个 m×n的矩阵 A，其F范数定义为：

参考资料：

        张凯院等编著. 矩阵论[M]. 西安：西北工业大学出版社，2017.