离散数学-集合论-关系的闭包、等价关系与划分和偏序关系（9）

关系的闭包、等价关系与划分和偏序关系

1 关系的闭包

定义:设R是非空集合A上的关系，R的自反（对称或传递）闭包是A上的关系R’,使得R‘满足以下条件：
（1）R’是自反的（对称的或传递的）
（2）$R\subseteq R’$
（3）对A上任何包含R的自反（对称或传递）关系R’'，有$R^{\prime }\subseteq R^{\prime \prime }$,R的自反闭包记作$r(R)$,对称闭包记作$s(R)$,传递闭包记作$t(R)$。
一般将R的自反闭包记作$r(R)$,对称闭包记作$s(R)$
,传递闭包记作$t(R)$。
定理：设R为A上的关系，则有：
（1）$r(R)=R\cup R^0$ $（R^0=I_A）$
（2）$s(R)=R\cup R^{-1}$
（3）$t(R)=R\cup R^2\cup R^3\cup \cdot \cdot \cdot \cdot$
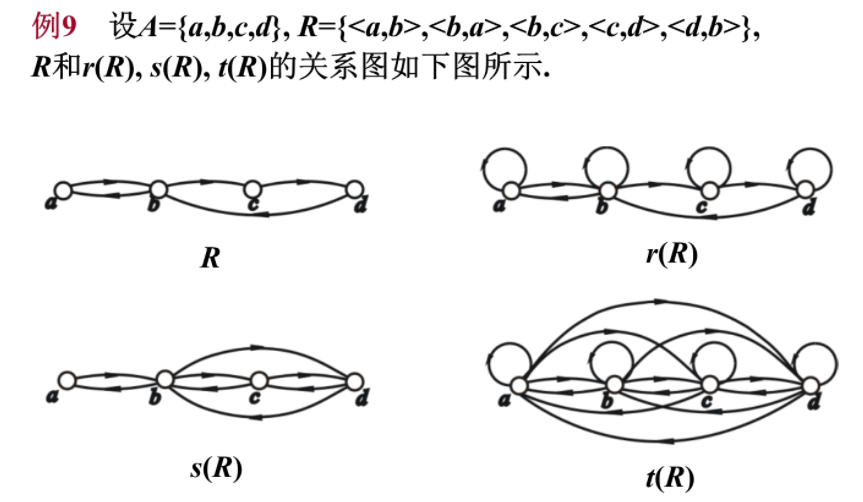
例如：给定A={1，2，3，4}和A上的关系R={<1,3>,<1,4>,<2,3>,<2,4>,< 3,4>}，求R的自反闭包、对称闭包和传递闭包。
解：
$r(R)$=R∪$I_A$
={<1,3>,<1,4>,<2,3>,<2,4>,< 3,4>}∪{<1,1>,<2,2>,< 3,3>.<4,4>}
={<1,1>,<2,2>,< 3,3>.<4,4>,<1,3>,<1,4>,<2,3>,<2,4>,< 3,4>}
$s(R)$=R∪$R^{-1}$
={<1,3>,<1,4>,<2,3>,<2,4>,< 3,4>}∪{< 3,1>,<4,1>,< 3,2>,<4,2>,<4,3>}
={< 3,1>,<4,1>,< 3,2>,<4,2>,<4,3>,<1,3>,<1,4>,<2,3>,<2,4>,< 3,4>}
$t(R)$=$R\cup R^2$
={<1,3>,<1,4>,<2,3>,<2,4>,< 3,4>}∪{<1,4>,<2,4>}
={<1,3>,<1,4>,<2,3>,<2,4>,< 3,4>,<2,4>}

2 等价关系和划分

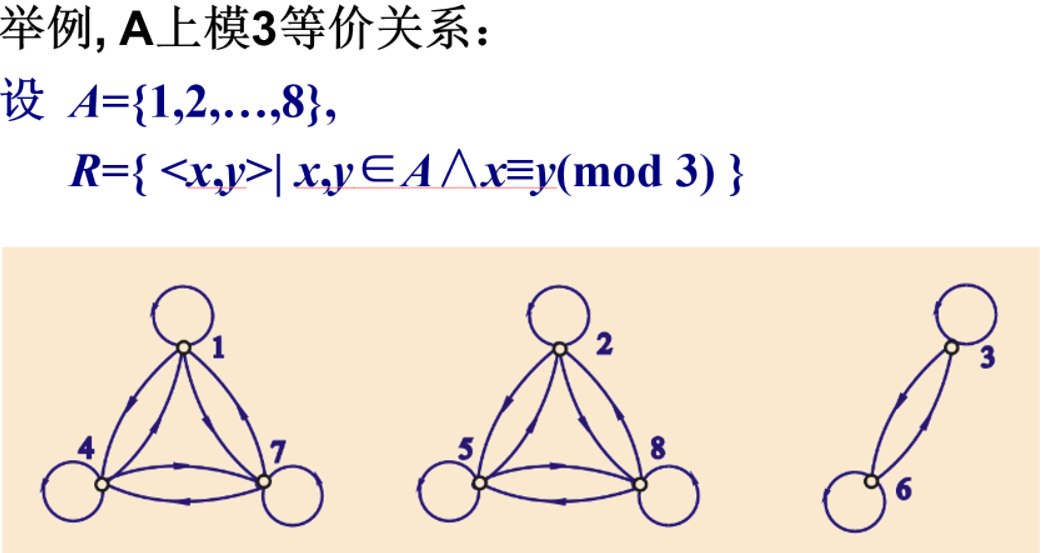
定义1：等价关系
设R为非空集合A上的关系，如果R是自反的、对称的和传递的，则称R为A上的等价关系，设R是一个等价关系，若<x,y>∈R，称x等价于y，记作x~y。

定义2：等价类
设R为非空集合A上的等价关系，$\forall x$∈A，令
$[x{]}_R=（y|y\in A\wedge xRy$
称[x]_R为关于R的等价类，简称为x的等价类，简记[x]或$\text{xˉ}$。

定义3：商集
设R为非空集合A上的等价关系，以R的所有等价类作为元素的集合称为A关于R的商集，记作A/R，即：
$A/R=[x{]}_R|x\in A$

定义4：集合的划分

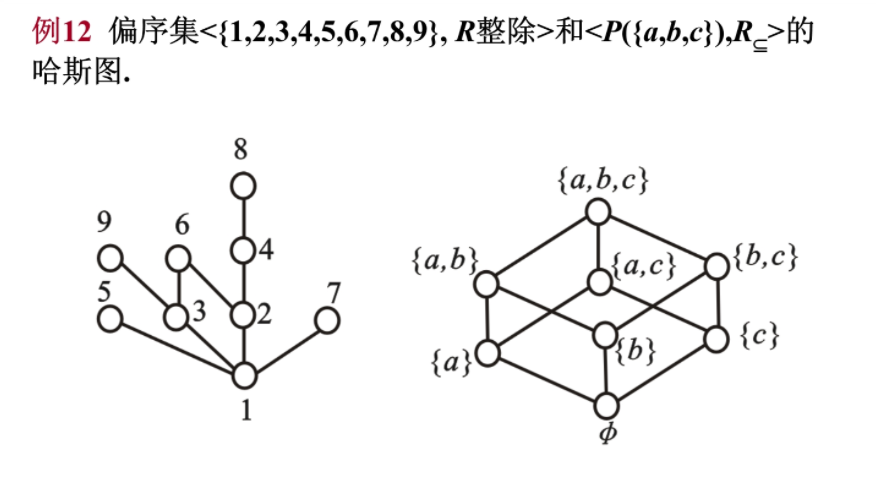
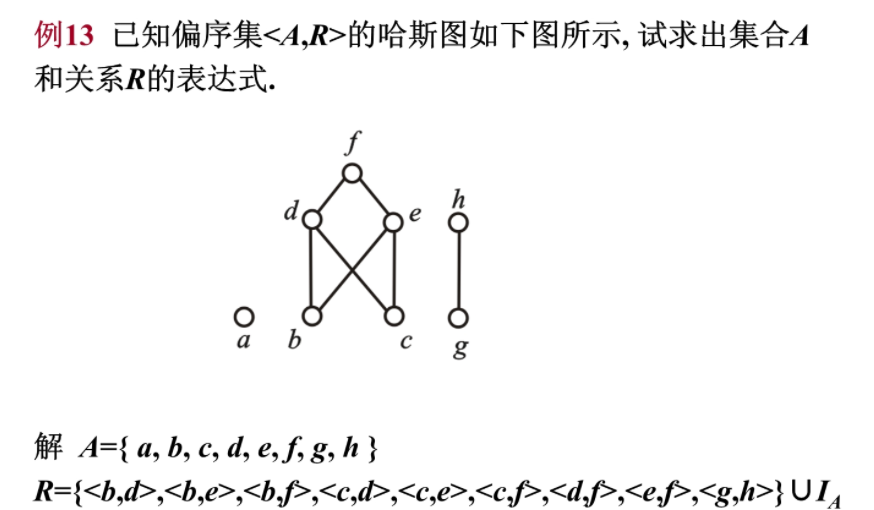
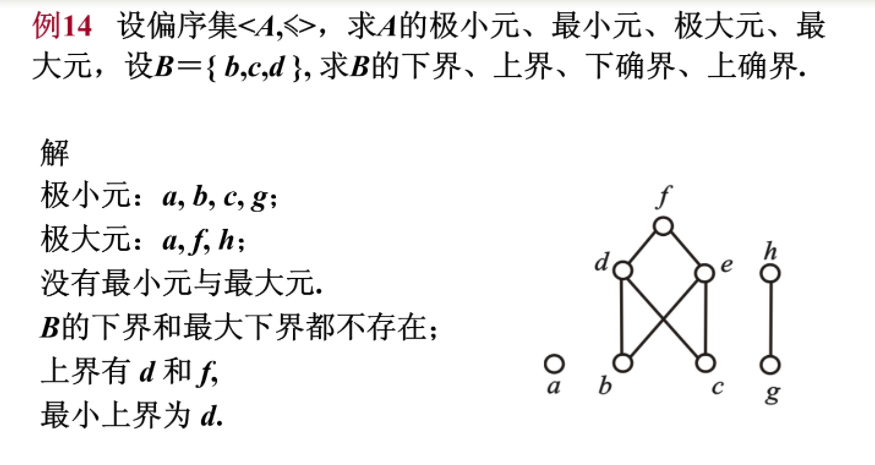
3 偏序关系