矩阵论-第三章：矩阵的标准型

1.哈密顿-凯莱定理

定义：每个 n 阶矩阵都是它的特征多项式的根
特征多项式：f(A) = |…|=…，λ 为特征值

2. 简化运算

又因为哈密顿-凯莱定理可知，f(A) = 0，所以化简后等于 r(A)

3.例题-简化矩阵计算

定义： 当你看到需要计算一个很长的公式的时候，你就可以往哈密顿-凯莱定理+简化计算上思考。
方法：

1. 利用求特征值的方法|…|得到形如 f(A) = A… 的方程。
2. 然后将长的计算公式假设为 φ(A)，然后除以 f(A)，得到余项，而 f(A) 本身就等于 0 ，所以 φ(A) ＝ 余项
   
   第二问求A逆
   方法： 第二问所求的 A-1，应该是一个包含 A 和 E 的表达式，我们可以利用求秩的表达式求解。——>将单独 E 想办法转到右边，A 进行提出，就能够很快速地求解 A-1 了
   
   第三问：求较长计算式的逆
   方法： 较长计算式一般等于余项，相当于求余项的逆，将余项往 |…| 公式里去凑即可**【凑+哈密顿-凯莱定理即可】**
   

4.最小多项式

概念上： 分为特征多项式（f(A)=|…|=…）、零化多项式、最小多项式；最小多项式相当于在零化多项式的基础至少，加了一个首项系数为1的条件。
特点上： 特征多项式和最小多项式的根完全一样，所以要找到最小多项式，首先得找到特征多项式，然后再加上一个条件即可。

5.例题-求最小多项式

从特征多项式——>最小多项式的关键：将矩阵代入多项式后，验证多项式的值是否为 0，为0，则证明满足最小多项式
如何验证是否为0 ？——> 将矩阵 A 和 E 代入到多项式中，如：(入-2)(入-4) ——>(A-2E)(A-4E)

6.Jordan 标准型

1.入矩阵：矩阵A的所有元素都是入的多项式：

2.行列式因子：
定义： A(入)矩阵为入矩阵，其中所有非零的 K 阶子式：| … |、| … |、| . | （值不为0的子式），其中首项系数为1，最大公因式为0的子式，为A的一个K阶行列式因子

3.初级因子：
就是将不变因子分解为互不相同的两个因子乘积，如：

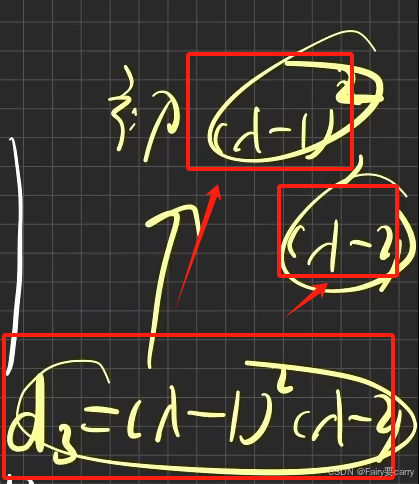
4.Jordan标准型的定义：

1. 约旦块与初级因子相关，而初级因子是由不变因子分解得来的，而不变因子是由行列式因子得来的，最后行列式因子和A(入)相关。
2. 注意，约旦标准型的构成与若干个约旦块有关，而约旦块的构造与若干个初级因子有关
   
   5.求解约旦标准型的方法：行列式因子法（利用初级因子）
   

7.例题：求解Jordan标准型

利用行列式因子求 Jordan 标准型
关键：

1. 求行列式因子，分为 K…k-1…1 阶行列式因子，如图所示
2. 子式的行列式因子有很多，其中最大公因子为其行列式因子
3. 行列式因子相除为不变因子
4. 初等因子为为1因子
   
   求得二阶行列式因子 D2
   
   求得一阶行列式因子 D1 （即求得一阶行列式的最大公因子 D3）
   
   此时已知三阶行列式因子、二阶行列式因子、一阶行列式因子，即可求得不变因子：
   
   然后利用不变因子拆分为初级因子：
   
   利用初级因子求得标准型：
   （入-k），标准型里面的值即为k
   
   思路：
   K阶行列式因子D1、D2、D3——>不变因子d1=D1，d2=D2/D1，d3=D3/D2——>初级因子【(入-k)^0不看，只需看非1的因子】
   注：初级因子为（入-k）^n代表n阶，里面的值为k，然后需要给上一层补上1，然后组合起来

8.史密斯Smith 标准型

史密斯标准型的中间元素就是不变因子
知识点：

• 任意一个非零多项式矩阵 A 都可以经过初等变换化为 Smith 标准型
• 具体步骤：确定矩阵左上角第一个元素 d1=D1 为一阶行列式因子——>然后将 d1 所在的行和列的其他元素消为 0 得到新矩阵 B1(入)——>将左上角作为 d2 ,重复反复
  

9.例子：Smith标准型

感觉Smith标准型就是考研里面求标准型不断消一层一层的其余元素，对角线元素就为秩

不断消去对角线的其余元素

例10：用史密斯标准型的方法求解约旦标准型

梳理一下思路： 首先求得(入E-A)的史密斯标准型，对角线内容为不变因子——>然后我们可以根据不变因子求得初级因子——>初级因子作为约旦块——>结合起来即可得到 Jordan 标准型
例题：
1.首先入E-A，经过初等行变换得到 Smith 标准型
2.Smith 标准型的中间元素都是不变因子，然后将这些不变因子转为初级因子，根据这些初级因子写出约旦标准型