动态规划（复习）

者半

已于 2024-05-23 22:42:40 修改

阅读量1k

点赞数 21

文章标签：动态规划算法

于 2024-04-07 10:17:48 首次发布

本文链接：https://blog.csdn.net/weixin_57140993/article/details/137448445

版权

本文介绍了动态规划的基础概念，包括最优子结构、无后效性和子问题重叠。通过实例展示了如何运用动态规划解决LIS、最长公共子序列、01背包等问题，并提供了模板题的解答过程。最后概述了树形动态规划的基本步骤。

摘要由CSDN通过智能技术生成

动态规划基础

能用动态规划解决的问题，需要满足三个条件：最优子结构，无后效性和子问题重叠。

最优子结构

证明问题最优解的第一个组成部分是做出一个选择；
对于一个给定问题，在其可能的第一步选择中，假定你已经知道哪种选择才会得到最优解。你现在并不关心这种选择具体是如何得到的，只是假定已经知道了这种选择；
给定可获得的最优解的选择后，确定这次选择会产生哪些子问题，以及如何最好地刻画子问题空间；
证明作为构成原问题最优解的组成部分，每个子问题的解就是它本身的最优解。方法是反证法，考虑加入某个子问题的解不是其自身的最优解，那么就可以从原问题的解中用该子问题的最优解替换掉当前的非最优解，从而得到原问题的一个更优的解，从而与原问题最优解的假设矛盾。

无后效性

已经求解的子问题，不会再受到后续决策的影响。

子问题重叠

如果有大量的重叠子问题，我们可以用空间将这些子问题的解存储下来，避免重复求解相同的子问题，从而提升效率。

基本思路

对于一个能用动态规划解决的问题，一般采用如下思路解决：

将原问题划分为若干阶段，每个阶段对应若干个子问题，提取这些子问题的特征（称之为状态）；
寻找每一个状态的可能决策，或者说是各状态间的相互转移方式（用数学的语言描述就是 状态转移方程）。
按顺序求解每一个阶段的问题。

LIS：最长上升子序列

子序列:原序列通过去除某些元素但不破坏余下元素的相对位置而形成的新序列。

比如原序列：[1,3,4,5,7,2]
子序列可以是[1,4,7,2],[3,4,5,2]
最长的上升子序列是[1,3,4,5,7]

状态是什么?

前i个数字的最长上升子序列?

这种状态没办法实现状态转移，因为不知道具体的序列是谁

以第i个数字结尾的最长上升子序列？

知道一个信息，知道尾部的信息，想要找递增的，可以根据尾部信息找下一个更大的。

dp[i]可以从dp[1],dp[2]...dp[i-1]转移过来

以1结尾，后面加个a[i]，以2结尾,后面加个a[i]，前提是a[i]要比它最后一个元素大。（前一个）

这么多状态可以转移过来，哪个是我要的？最大的状态才是我们要的。

dp[i] = max(dp[j] + 1), j < i && a[j] < a[i]}

也就是在a[j]后面加个a[i]

比如我想找以这个3结尾的最长上升子序列：

、

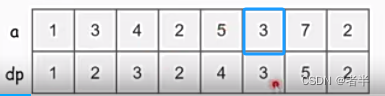在a中前面比3小的有1和2，挑选其中dp值最大的那个，加一（也就是在末尾新加一个元素）

模板题：

蓝桥2049

import os
import sys

# 请在此输入您的代码
n = int(input())
a = [0] + list(map(int, input().split()))
dp = [0] * (n + 1)
for i in range(1, n + 1):
  dp[i] = 1 # 以每个字符结尾的子序列至少包括它自己。
  for j in range(1, i): # 在前面的下标中，寻找最长的子序列，在此基础上+1
    if a[j] < a[i]: # 如果j小于当前字符i，说明可以由j转移过来
      dp[i] = max(dp[j] + 1, dp[i]) # 比较每个状态转移，选取最大的。
print(max(dp))

蓝桥742

import os
import sys

# 请在此输入您的代码
n = int(input())
a = [0] + list(map(int, input().split()))
dp1 = [0] * (n + 1) 
dp2 = [0] * (n + 1) # 从i出发的最长下降子序列
for i in range(1, n + 1):
  dp1[i] = 1
  dp2[i] = 1
  for j in range(1, i):
    if a[j] < a[i]:
      dp1[i] = max(dp1[i], dp1[j] + 1)
for i in range(n, 0, -1): # 从后往前遍历
  for j in range(i + 1, n + 1):
    if a[j] < a[i]:
      dp2[i] = max(dp2[i], dp2[j] + 1)

ans = max([dp1[i] + dp2[i] - 1 for i in range(1, n + 1)])
print(n - ans)

LCS：最长公共子序列

给定一个长度为N的数组a和长度为M的数组b，求最长公共子序列

公共子序列:数组a和b中均包含该子序列。

状态:dp[i][j]:a数组前i个，b数组前j个的最长公共子序列长度

边界:dp[0][0]= dp[..][0]= dp[0][..]= 0

状态转移方程:

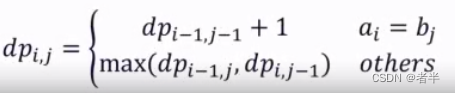
a[i] == b[j]，转移过来，要么从左边，要么从上边，要么从左上角转移过来。

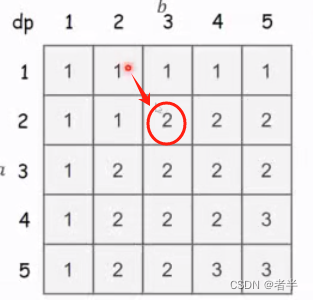
如何求出具体的公共子序列:从(n,m)往回走，如果往上、往左DP值不变则直接走，否则往左上方走，记录子序列。

比如这边：a4 == b5

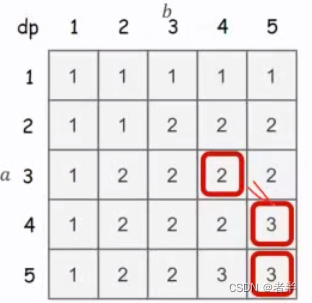
模板题：

蓝桥1189

import os
import sys

# 请在此输入您的代码
n, m = map(int, input().split())
a = [0] + list(map(int, input().split()))
b = [0] + list(map(int, input().split()))
dp = [[0] * (m + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
  for j in range(1, m + 1):
    if a[i] == b[j]:
      dp[i][j] = dp[i - 1][j - 1] + 1
    else:
      dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

print(dp[n][m])

扩展：想知道具体的最长公共子序列

ans = []
x, y = n, m
while x != 0 and y != 0:
    if dp[x][y] == dp[x - 1][y]:
        x -= 1
    elif dp[x][y] == dp[x][y - 1]:
        y -= 1
    else:
        ans.append(a[x])
        x -= 1
        y -= 1
print(ans[::-1])

a和b

输出：

01背包

给定一个容积为v的背包，现有N件物品，第i件物品的体积为wi，价值为vi。每件物品智能拿或不拿，请拿出体积总和不超过v的最大价值。

贪心策略可以吗？

V = 6，三件物品，体积分别为1，3，5，价值分别为10，20，30.按照性价比肯定优先选择1之后选择体积3，总价值是30实际上选择1.5才是最优的。

状态：dp[i][j]：前i件物品，体积为j的最大价值。

每件物品只有两种情况，拿和不拿，实际上求的就是拿这个物品更大还是不拿这个物品更大。

$dp[i][j] = dp[i - 1][j],j < w[i]$

$dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - w[i]] + v[i]),j >= w[i]$

第一个维度从小到大，第二个不care

边界：dp[0][0] = dp[0][...] = dp[...][0]

滚动数组优化：转移方程种，第i行的更新，仅和第i-1行有关系，因此可以使用滚动数组。节省空间，奇数的用偶数更新，偶数用奇数更新

模板题：

蓝桥1174

import os
import sys

# 请在此输入您的代码
N, V = map(int, input().split())
dp = [[0] * (V + 1) for i in range(N + 1)]
for i in range(1, N + 1):
  wi, vi = map(int, input().split())
  for j in range(0, V + 1):
    if j < wi:
      dp[i][j] = dp[i - 1][j]
    else:
      dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - wi] + vi)

print(dp[N][V])

滚动数组优化，实际上就是把第一维度的全部模2，只需要2 * (v + 1)的数组

偶数行的就用奇数行更新，因为i肯定由i-1行更新

n, v = map(int, input().split())
dp = [[0] * (v + 1) for _ in range(2)]
for i in range(1, n + 1):
  w, vi = map(int, input().split())
  for j in range(v + 1):
    if j < w:
      dp[i % 2][j] = dp[(i - 1) % 2][j]
    else:
      dp[i % 2][j] = max(dp[(i - 1) % 2][j], dp[(i - 1) % 2][j - w] + vi)

print(dp[n % 2][v])

最终优化：只需要（t + 1）* 1的dp数组

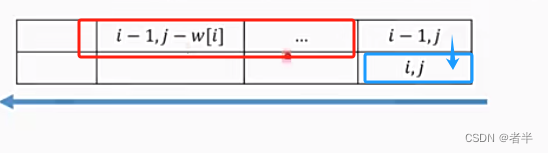
更新dp[i][j]时，用到的是上一行对应位置(dp[i-1][j])和上一行先前位置(dp{i-1][j-w[i]])的元素，因此可以使用单个数组进行更新:直接从大到小对dp数组进行覆盖即可

为什么从大到小遍历？因为求dp[i][j]要dp[i-1]行的前面的这些值更新，如果你从小到大遍历，第i-1行会被当前i行给覆盖掉。

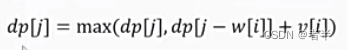
n, v = map(int, input().split())
dp = [0] * (v + 1)
for i in range(1, n + 1):
  w, vi = map(int, input().split())
  for j in range(v, w - 1, -1):
      dp[j] = max(dp[j], dp[j - w] + vi)

print(dp[v])

完全背包：

给定一个容积为v的背包，现在有N种物品，第i种物品的体积为wi，价值为vi，每种物品有无限件，请求出体积总和不超过V的最大价值

状态：dp[i][j]：前i种物品，体积为j的最大价值。

对于第i种物品：

dp[i][j] = dp[i - 1][j] 不拿
dp[i][j] =dp[i - 1][j - wi] + vi 拿一件
dp[i][j] =dp[i - 1][j - 2wi] + 2vi]拿两件
dp[i][j] = dp[i - 1][j - ki] + k * vi]拿k件

三重循环，第一层i，第二层j，第三层k

时间复杂度高，O（N*V*V）

$dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - k * wi] + k * vi]),k=1,2,....j/wi$

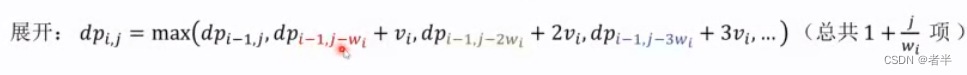
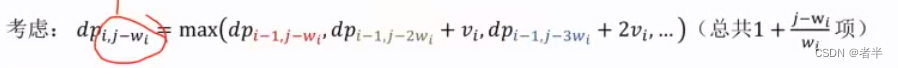
把dp[i][j-wi]带入dp[i][j]

简化： $dp[i][j] = max(dp[i - 1][j], dp[i][j - wi] + vi)$

直观上的理解：前一项表示不取第i种，后一项表示在先前的基础上取第i种因为可以取多次。

模板题

蓝桥1175

import os
import sys

# 请在此输入您的代码
N, V = map(int, input().split())
dp = [[0] * (V + 1) for i in range(N + 1)]

for i in range(1, N + 1):
  wi, vi = map(int, input().split())
  for j in range(0, V + 1):
    if j < wi:
      dp[i][j] = dp[i - 1][j]
    else:
      dp[i][j] = max(dp[i - 1][j], dp[i][j - wi] + vi)
print(dp[N][V])

优化：

和01背包不同的是遍历方向，完全背包是从小到大。

import os
import sys

# 请在此输入您的代码
n, v  = map(int, input().split())
dp = [0] * (v + 1)

for i in range(1, n + 1):
  wi, vi = map(int, input().split())
  for j in range(wi, v + 1):
      dp[j] = max(dp[j], dp[j - wi] + vi)

print(dp[v]) # O(n * v)

多重背包

模板题:

蓝桥1176

import os
import sys

# 请在此输入您的代码
N, V = map(int, input().split())
dp = [[0] * (V + 1) for i in range(N + 1)]
for i in range(1, N + 1):
  wi, vi, si= map(int, input().split())
  for j in range(0, V + 1):
    for k in range(0, min(si, j // wi) + 1):
      dp[i][j] = max(dp[i][j], dp[i - 1][j - k * wi] + k * vi)

print(dp[N][V])

将多重背包转换为01背包问题，原始策略是将S件同类型物品都看作单独的物品，然后逐个放入01背包进行选择，但是时间复杂度没有改变

新策略：二进制拆分S

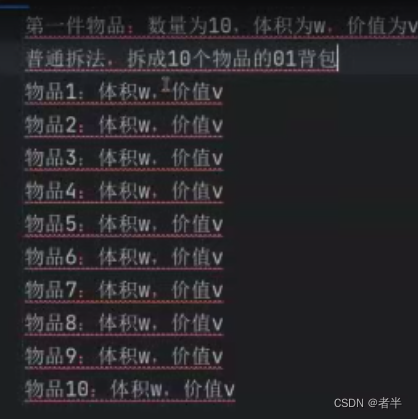
N, V = map(int, input().split())

w_v = []
for i in range(N):
  wi, vi, si = map(int, input().split())
  k = 1
  while si >= k:
    w_v.append((k * wi, k * vi))
    si -= k
    k *= 2
  if si != 0:
    w_v.append((si * wi, si * vi))

dp = [0] * (V + 1)
for i, (w, v) in enumerate(w_v):
  for j in range(V, w - 1, -1):
    dp[j] = max(dp[j], dp[j - w] + v)

print(dp[V])

二维费用背包

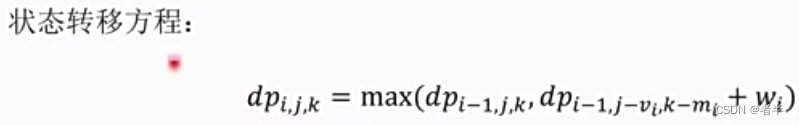
时间上能过，但是空间未必能过。

模板题：

蓝桥3937

import os
import sys

# 请在此输入您的代码
N, V, M = map(int, input().split())
dp = [[0] * (M + 1) for i in range(V + 1)]

# 前i件物品
for i in range(1, N + 1):
  # vi体积，mi重量，wi价值
  vi, mi, wi = map(int, input().split())
  for j in range(V, vi - 1, -1):
    for k in range(M, mi - 1, -1):
        dp[j][k] = max(dp[j][k], dp[j - vi][k - mi] + wi)

print(dp[V][M])

分组背包

和01背包不同的点在于每组的每件物品都要更新

模板题：

蓝桥1178

import os
import sys

# 请在此输入您的代码
N, V = map(int, input().split())
dp = [[0] * (V + 1) for i in range(N + 1)]

for i in range(1, N + 1):
  each_group = []
  s = int(input())
  for _ in range(s):
    w, v = map(int, input().split())
    for j in range(V + 1):
      if j < w:
        dp[i][j] = max(dp[i][j], dp[i - 1][j])
      else:
        dp[i][j] = max(dp[i][j], dp[i - 1][j], dp[i - 1][j - w] + v)
  
print(dp[N][V])

优化

# 滚动数组优化
N, V = map(int, input().split())
dp = [0] * (V + 1)

groups = []
for i in range(1, N + 1):
  s = int(input())
  each_group = [list(map(int, input().split())) for k in range(s)]
  groups.append(each_group)

# 枚举每一组
for i in range(1, N + 1):
  # 枚举每一种体积
  for j in range(V, -1, -1):
    for w, v in groups[i - 1]:
      if j >= w:
        dp[j] = max(dp[j], dp[j - w] + v)
print(dp[V])

树形dp

基础知识：

蓝桥1319

n = int(input())
happy = [0] + list(map(int, input().split()))
tree = [[] for _ in range(n + 1)]
fa = [0] * (n + 1)
dp = [[0, happy[i]] for i in range(n + 1)]
for i in range(n - 1):
  u, v = map(int, input().split())
  tree[v].append(u)
  fa[u] = 1

def dfs(v):
  for u in tree[v]:
    dfs(u)
    dp[v][1] += dp[u][0]
    dp[v][0] += max(dp[u][0], dp[u][1])

root = 0
for i in range(1, n + 1):
  if not fa[i]:
    root = i

dfs(root)
ans = max(dp[root][0], dp[root][1])
print(ans)

蓝桥3891

import sys
sys.setrecursionlimit(100000)
n, m = map(int, input().split())
G = [[] for _ in range(n + 1)]
fa = [0] * (n + 1)
vis = [0] * (n + 1)
dp = [[0, i] for i in range(n + 1)]
for _ in range(n - 1):
  l, r = map(int, input().split())
  G[r].append(l)
  fa[l] = 1

def dfs(v):
  # 记录每个点的字数结点数
  dp[v][0] = -1 # 1改成-1
  vis[v] = 1
  for u in G[v]:
    if vis[u] == 0:
      dfs(u)
      dp[v][0] += dp[u][0]

root = 0
for i in range(1, n + 1):
  if not fa[i]:
    root = i

dfs(root)
dp.sort()
for i, (x, y) in enumerate(dp, 1):
  if y == m:
    print(i)
    break

小总结：

树形dp基本步骤：

正在更新...

者半

关注

21
点赞
踩
12

收藏

觉得还不错? 一键收藏
0
评论
动态规划（复习）

子序列:原序列通过去除某些元素但不破坏余下元素的相对位置而形成的新序列。状态是什么?前i个数字的最长上升子序列?这种状态没办法实现，因为不知道具体的序列是谁以第i个数字的最长上升子序列？知道一个信息，知道尾部的信息，想要找递增的，可以根据找下一个更大的。dp[i]可以从dp[1],dp[2]...dp[i-1]转移过来以1结尾，后面加个a[i]，以2结尾,后面加个a[i]，前提是a[i]要比它最后一个元素大。（前一个）这么多状态可以转移过来，哪个是我要的？才是我们要的。
复制链接

扫一扫