前言:
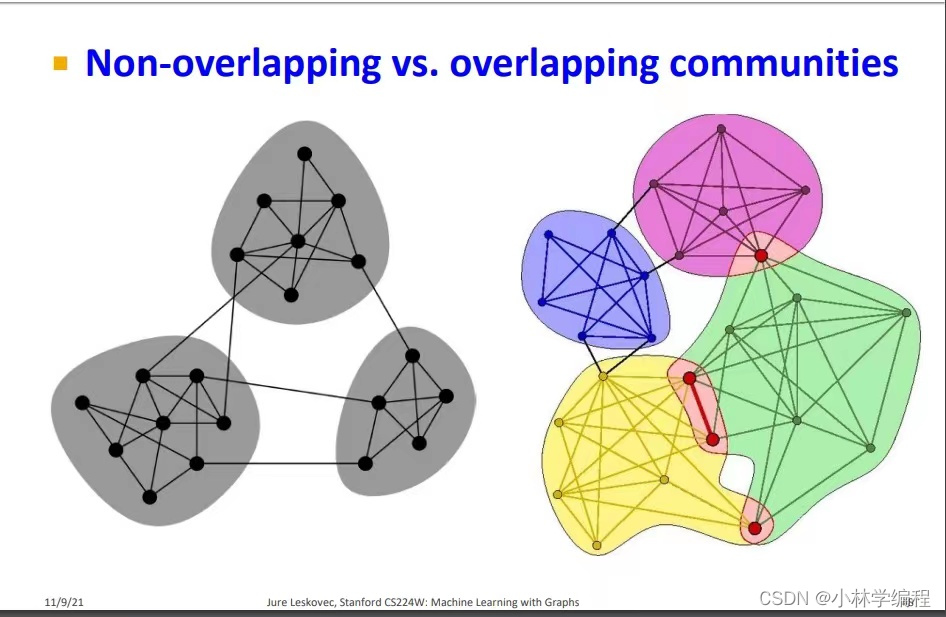
我们在(一)中讲了‘network communites’是什么和目标函数的建立,在(二)讲了怎么样计算出每一个集群的louvain算法。当我们在讲louvain算法时,我们计算出来的每两个集群之间都没有相互重叠的部分(如下图对比),那我们的(三)中就讲述了如果集群与集群之间有重叠该用什么算法计算?
一:BigCLAM算法的建立
(1):给graph建立一个基于节点社区从属的一个泛化模型(Community Affilication Model)(AGM)
(2):给出一张实际的graph,假设这张真实graph是由我们的泛化模型(AGE)生成的,然后更新模型找到可以生成该graph效果最好的AGE模型。
二:AGE模型的建立
我们应该建立怎么样的AGE模型呢?或者说AGE模型长什么样子呢?如下图左图
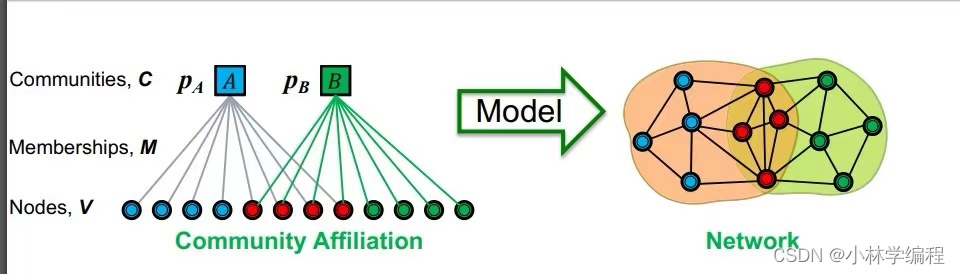
并且定义了一些新的量:V表示节点,M表示从属关系(表示该节点属于哪个集群中),C表示集群的集合,而和
则表示每一个集群的一个概率(是以一个矩阵参数表示的)是用来描述在这个集群内的两点间连接在一起的概率。我们也可以从右图中也可以直观的看出之间的关系。
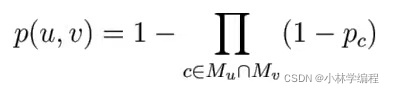
所以,现在已经定义了四个量(V,C,M,{})(其中
为上面
及其他集群p的合称),我们可以定义如上图公式。
ps:p(u,v)表示u,v两节点之间连接的概率,而连乘符号下面的一串则表示u,v一共属于几个集群(例如取第一张图片的红色点为例(u,v都属于红色点),那么连乘就要乘以两项,因为他们两个节点并一起总共有两个集群)
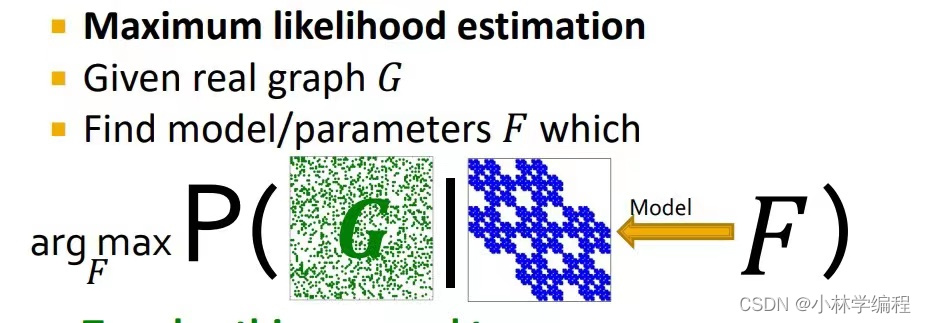
现如上图所示,在我们已经拥有了graph中任意两节点之间相连的概率,所以现在我们需要构建一个模型(称为F)让它生成一张graph的前提下,使这张graph与所给的真实graph要相互接近,并且最大化参数F。
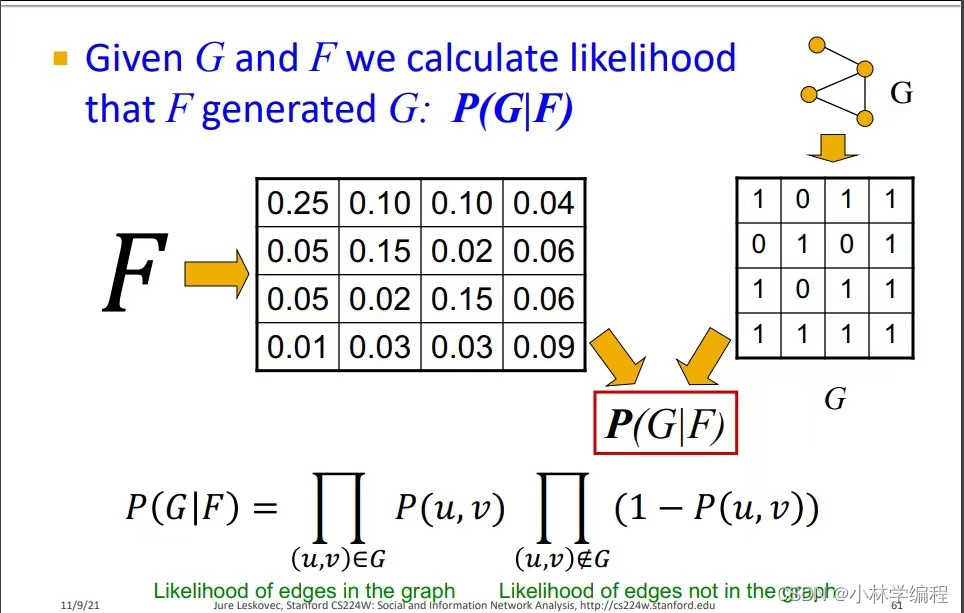
我们怎么样定义一个具体的函数呢?如上图所示,图中左侧为模型F提供的邻接矩阵的连接概率图,右侧为真实的graph的邻接矩阵,把他们两个结合在一起形成了下面的公式。直觉上来看,P(G|F)把真实的graph中,有连接和没有连接的节点之间拆了开来,有连接的两个节点就概率直接相乘,没有连接的两个节点之间就是先用1-两节点的概率在相乘,得到的结果(不断地跟新F的参数)就是P(G|F)的概率上升,使F模型生成的graph越来越接近给定的真实的graph。
到现在我们已经定义了P(u,v)和P(G|F),但我们注意到我们还没有定义具体该怎么算,定义之前,我们先定义一个参量
,
表示u节点对属于该集群c的连接强度(可以这么理解一个参数,比如虽然大家基本上都属于一个家庭,不过每个家庭给孩子的归属感不同,这里的每个家庭就可以看做是一个集群,孩子看做集群中的节点,归属感就是
)如下图给出。
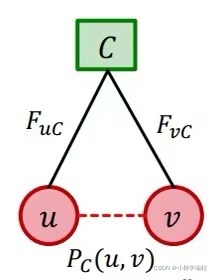
现在我们就可以定义一个啦!如下图

直觉上看就是和
越大,他们之间的
也就越大。
有了如上的公式后,我们就可以扩大P(u,v)的算法啦,如下图:

表示集群c得集合。
之后将简化后的P(u,v)带入我们上面定义的P(G|F)中得到下图公式,再将得到的结果对数化,从而得到我们的目标函数:


现在我们用梯度下降的方式来优化目标函数如下图公式:

为什么图中第一个公式中的第二个连加符号中的内容需要扩展到图中的第二个公式呢?
这是为了减轻计算的代价。
以上就是我们BigCLAM算法的全部内容啦!
系列结束!
三:参考视频:
1:cs224w图机器学习的第13章节:【斯坦福 CS224W】图机器学习( 中英字幕 | 2021秋) Machine Learning with Graphs by Jure Leskovec_哔哩哔哩_bilibili







 本文介绍了BigCLAM算法,通过构建CommunityAffiliationModel (AGM) 和AGE模型来处理社区重叠问题。文章详细解释了概率模型P(G|F)和参数优化过程,展示了如何利用节点归属强度和概率连接计算目标函数。涉及关键概念如P(u, v)和梯度下降优化。
本文介绍了BigCLAM算法,通过构建CommunityAffiliationModel (AGM) 和AGE模型来处理社区重叠问题。文章详细解释了概率模型P(G|F)和参数优化过程,展示了如何利用节点归属强度和概率连接计算目标函数。涉及关键概念如P(u, v)和梯度下降优化。
 https://blog.csdn.net/weixin_57643648/article/details/123545748?spm=1001.2014.3001.5501
https://blog.csdn.net/weixin_57643648/article/details/123545748?spm=1001.2014.3001.5501 https://blog.csdn.net/weixin_57643648/article/details/123589236?spm=1001.2014.3001.5501
https://blog.csdn.net/weixin_57643648/article/details/123589236?spm=1001.2014.3001.5501
















 3134
3134

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










