目录
1.车辆模型
在自动驾驶汽车的轨迹跟踪控制研究中,建立能够准确反映车辆实际运动规律的精确车辆模型是实现轨迹稳定性和精确跟踪的基础。
1.1车辆运动学模型
车辆运动学模型基于平面几何关系,在车辆低速行驶状态下可以准确地描述车辆的行驶位姿信息,该模型设计的控制器结构简单,实时性高,但在高速情况和连续曲率变换下,容易造成轨迹跟踪失败。因此本文假设车辆为刚体,忽略轮胎的侧偏影响,忽略车辆没有绕Y轴的俯仰及绕X轴的翻滚等影响,假设车辆的运动是一个二维平面的运动,假设车辆运动和转向都是前轮转向,最终可将车辆横向运动学模型简化为如图1-1所示的自行车运动学模型。
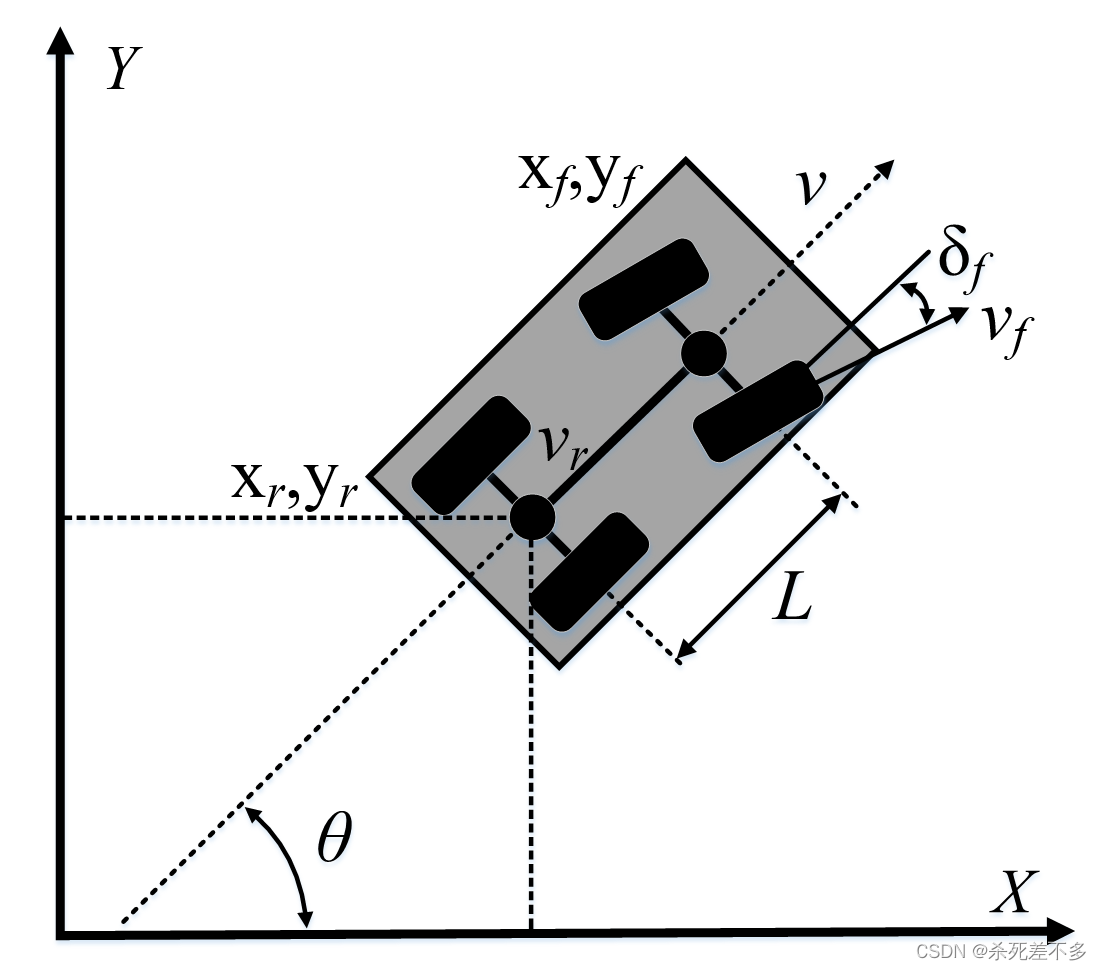
图1-1 车辆运动学模型
其中为前轮转角;
和
分别为前轴轴心和后轴轴心的坐标;
为前轴轴心速度,
为后轴轴心速度;
为轴距;
为航向角。
在后轴行驶轴心处,速度为:
前后轴的运动学约束为:
联立上述两式可得:
最终可得车辆横摆角速度为:
综上所述,得到车辆的运动学模型状态方程为:
1.2车辆单轨动力学模型
考虑到无人驾驶车辆在不同车速下车辆轮胎受到的横向、纵向接触的力不同,并为减少控制器的计算量,采用了可以反应车辆侧向运动的单轨二自由度侧向动力学简化模型。在单轨二自由度动力学模型下,假设车辆行驶时只考虑轮胎侧偏特性,忽略车辆Z轴的位移变化,忽略车辆横纵向空气动力学的影响,建立如图1-2单轨二自由度动力学模型。

1-2单轨线性二自由度动力学模型
在假设转向小角度及轮胎动力学的基础上,车辆动力学模型采用简化车辆单轨线性二自由度动力学模型。
车身轴方向应用牛顿第二定律可得:
其中,为车辆总质量,
是车辆质心处的横向加速度,
、
为地面给前轮胎和后轮施加的横向力。横向加速度
由两部分组成:车辆沿车身
轴横向运动产生的横向加速度
,车身横摆运动产生的向心加速度
,可得:
其中,为车辆的横向加速度,
为车辆纵向速度,
为车辆横摆角速度。
车辆绕轴的转矩平衡方程为:
对于轮胎受到的两个横向力,考虑到小侧偏角的假设,则地面施加给轮胎的横向力(侧偏力)与轮胎侧偏角成线性关系。
前轮侧偏角为:
其中,是前轮胎速度方向与车身纵轴的夹角,
为前轮转向角。
最终可得前后轮的横向轮胎力为:
其中,为前轮轮胎侧偏刚度,
为后轮轮胎侧偏刚度。
假设车轮质心到车轮的这一部分为刚体,根据刚体运动学则有:
基于小角度假设,可得:
以车辆横向位置、横向位置变化率、横摆角、横摆角变化率作为状态输入状态量。
横向位置变化率:
横摆角变化率:
最终可得状态空间方程为:
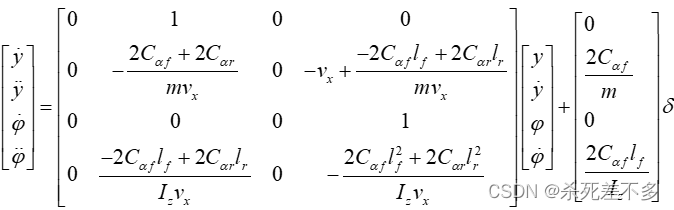
1.3车辆整车平面四轮动力学模型
整车平面四轮动力学模型是设计车辆轨迹跟踪控制器的基础。为了更好地研究轨迹跟踪稳定性问题,减少控制算法的计算量,对车辆的动力学模型进行了适当的简化。如忽略了车辆侧倾,俯仰运动对车辆的影响等。图1-3为建立的整车平面四轮动力学模型,根据该模型可建立车辆沿x轴,y轴和绕z轴的非线性动力学方程。

1-3整车平面四轮动力学模型
车辆沿x轴方向的纵向动力学方程:

车辆沿y轴方向的横向动力学方程:

车辆绕z轴方向的横摆力矩动力学方程:

式中,为整车质量;
,
,
分别为车辆坐标系下的横摆角速度,纵向速度和侧向速度;
为前轮转角,
是车辆的质心侧偏角;
是车辆绕z轴转动惯量;
为分别为车辆质心C.G到前轴和后轴的距离(* =f (前),r (后));
代表前轮和后轮的轮距(* =f,r);
和
分别为四个车轮的侧向力和纵向力(ij=fl (左前轮), fr (右前轮), rl (左后轮), rr (右后轮))。
车辆相对于全局坐标系下的运动平衡方程可以表示为:

式中,车辆的航向角,
和
分别为全局坐标系下的纵向速度和侧向速度。
车轮滑移率的计算表达式如下:
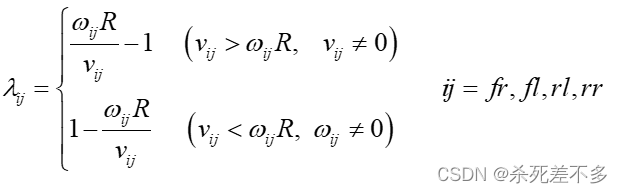
采用线性表达式计算轮胎的纵向力和侧向力
,具体表达式如下:

式中,、
分别为前后轮侧偏刚度,
、
分别为前后轮纵向刚度
1.4侧倾动力学模型
介绍的车辆平面动力学模型由于只能对车辆的横摆角速度和质心侧偏角进行控制已无法满足防侧翻控制的需求,因此需要建立整车侧倾动力学模型。该模型包括了等效侧倾刚度、等效阻尼系数、簧载质量等可以影响车辆侧倾稳定性的主要参数。图1-4为建立的整车侧倾动力学模型。

1-4为整车侧倾动力学模型
车辆侧倾运动动力学方程:

式中,是车辆绕x轴转动惯量;
是车辆质心C
.G到侧倾中心的距离,是车辆的簧载质量,
是悬架的等效侧倾刚度,
是悬架的等效阻尼系数,
是侧倾角,
是侧倾角速度,
是侧倾角加速度。
针对整车四轮动力学的前四个公式构架非线性方程:

式中,状态量 ,控制量
将非线性状态方程进行线性化处理,采用线性化控制方法设计轨迹跟踪控制器。
采用泰勒展开式,将非线性状态方程选取点进行线性化处理,线性化后的表达式如下:

2.离散化方法介绍
经线性化处理过后的状态是一种连续方程,由于多数的轨迹跟踪算法时一种离散时间控制方法,因此还需进行离散化处理,选取的状态方程如下所示:

2.1前向欧拉离散法
对上诉线性状态空间方程进行前向欧拉离散化,T=0.01,可得:


2.2中点欧拉离散法
对上述状态空间方程在区间积分可得:
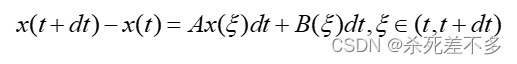
对于项,采用中点欧拉法对其进行离散化,可得:

对于,采用向前欧拉法进行离散化,可得:

最终可得:
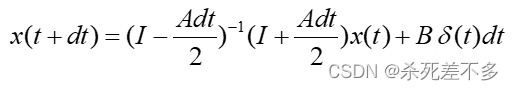
2.3双线性变换离散法
对上述状态空间方程离散化:
其中E为单位矩阵,T为离散时间。
2.4一阶差商法
以整车平面四轮动力学方程为例:


令![]()
可得:


3.常用轨迹跟踪算法
针对常用轨迹跟踪算法,如基于运动学LQR算法、Stanely算法、基于预瞄PID控制算法、基于几何模型的纯跟踪算法进行概述。
3.1斯坦利轨迹跟踪算法
斯坦利算法(Stanley)方法是一种基于横向跟踪误差的非线性反馈函数[1],其模型原理如图3-所示。

图3-1斯坦利模型原理示意图
在不考虑横向跟踪误差的情况,前轮偏角应当与给定期望轨迹的投影点的切线方向一致。其中示车辆航向与最近参考点切线方向之间的夹角,在没有任何横向误差的情况下,前轮方向与所在路径点的方向相同[2]。
在不考虑航向跟踪误差的情况下,横向跟踪误差越大,前轮转角越大,假设车辆预期轨迹在距离前轮
处与给定参考轨迹上最近点切线相交,根据几何关系得出如下非线性比例函数:
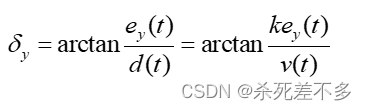
假设,其中
表示从从点行
驶到点
的距离,与车辆的车速有关,
为速度增益系数,可得:
此外,横向误差变化率:
由几何关系可知:

最终可得:

3.2基于预瞄的PID跟踪算法
预瞄控制是提高车辆横向控制鲁棒性和稳定性最好的方法之一。因此,采用预瞄控制思想,即以车辆前方预瞄点处的运动状态作为反馈设计PID控制器,预瞄时距T,预瞄距离由以下公式计算:

车辆当前时刻的位置为,预瞄点的位置表示为
,可得两点之间的坐标关系为:

横向误差计算
![]()
其中,为距离预瞄点
最近的轨迹点。
航向误差计算:

以横向误差和航向误差
作为反馈对方向盘转角或前轮转角进行PID控制:

其中,、
、
其中,分别为误差的比例系数、积分系数和微分系数,
。
3.3纯跟踪算法
纯跟踪算法作为一种经典的横向控算法,鲁棒性较好,可以获得比较良好的横向控制效果[68]。基于阿克曼模型,通过几何关系计算出预瞄点与车辆位置的关系,进而计算出转弯半径,从而获得前轮转角,纯跟踪算法原理如图3-2所示。

图3-2纯跟踪算法几何模型
在三角形AOC中,由数学公式可得:

化简可得:

在阿克曼转向系统中,前轮转角的关系与轴距和转弯半径有关,可得:

联立上列式子可得:

定义横向误差为当前车辆位姿和预瞄点在横向上的误差,可得:

考虑小角度假设,则有

3.4基于运动学模型的LQR算法
LQR理论作为现代控制理论发展最早最成熟的状态空间设计法之一,其控制对象是以状态空间形式给出的线性系统,目标函数为对象状态和控制输入的二次型函数。对于线性系统的控制器设计问题,如果其性能指标是状态变量和(或)控制变量的二次型函数的积分,则这种动态系统的最优化问题称为线性系统二次型性能指标的最优控制问题,简称为线性二次型最优控制问题或线性二次问题[64],其控制原理框架如下图所示。

图3-3LQR控制原理框架
假设一个线性系统的状态空间表示为:
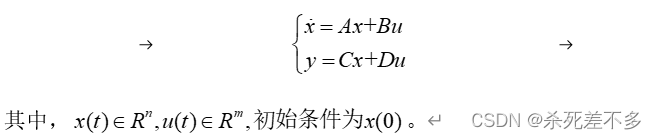
就上述线性系统,为确保其能够达到期望状态的稳定性能,设计最优状态反馈控制器:
将其带入上式,简化可得:

引入状态反馈后,线性系统的传递函数的极点为行列式的特征值,如是
稳定的,那么存在一个正定矩阵P,使得同时满足状态量足够小(系统达到稳定状态),控制量足够小(控制量尽量小)。
构造带约束的拉格朗日乘子代价函数:

假设代价函数J需要达到最小值,即达到了系统稳态,那么则有:

由上式可知,随着时间的推移,需要对系统施加的控制量会越来越小,即用最小的控制量使得系统达到了稳定控制状态。总体来说,Q矩阵的参数值增大,意味着这个参数作用的系统状态量将以更快的速度衰减到0,另一方面,R矩阵的参数值增大,意味着这个参数作用的控制量减小,控制器执行更少的动作,系统的状态衰减将变慢。因此,Q和R矩阵的参数选取要根据实际应用场景进行不断调试。

对上式进行偏导数求导,令其偏导数为0即可得到最优解,即:

最终可得:


经前向欧拉法离散化,可得:

3.5基于动力学模型的LQR算法



综上所述,车辆横向动力学模型跟踪误差状态空间方程为:
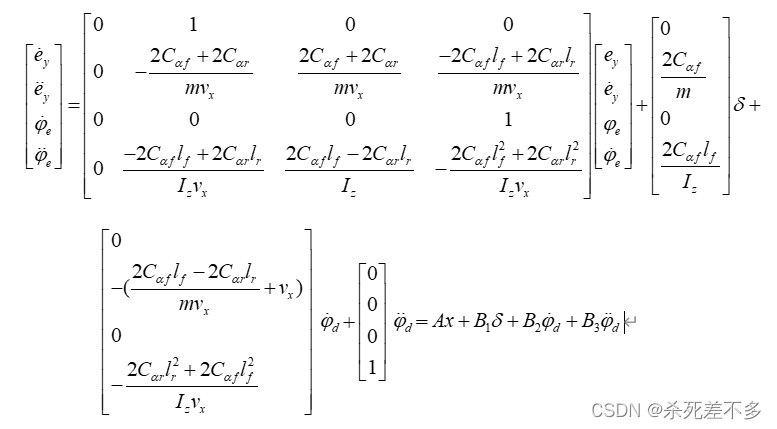







3.6MPC轨迹跟踪算法
针对如下运动学模型:

经过前向欧拉法离散化可得:

构建新的状态向量:
可得:
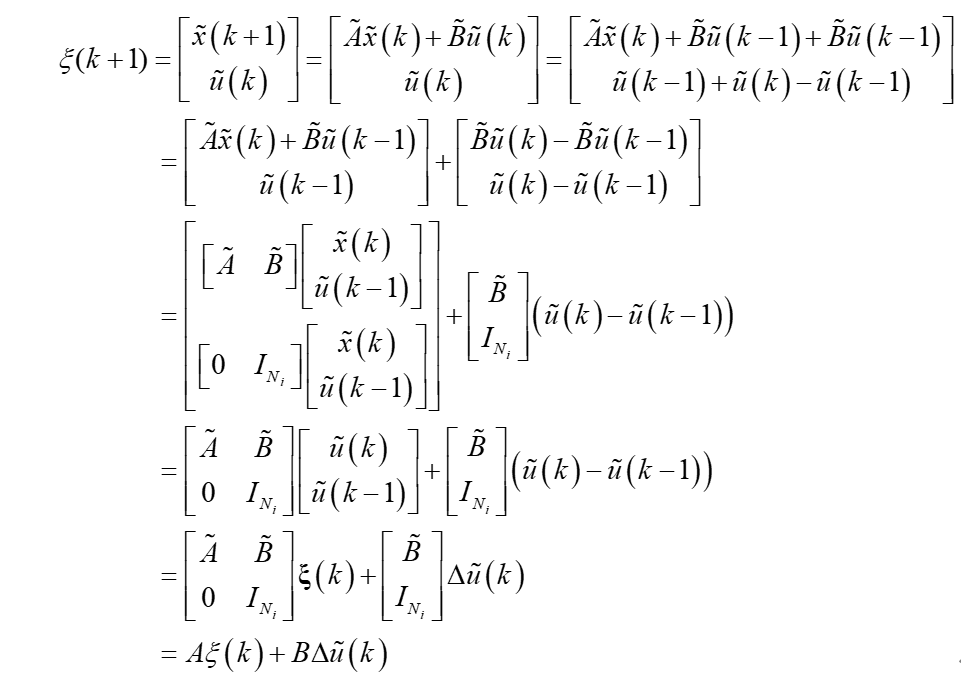
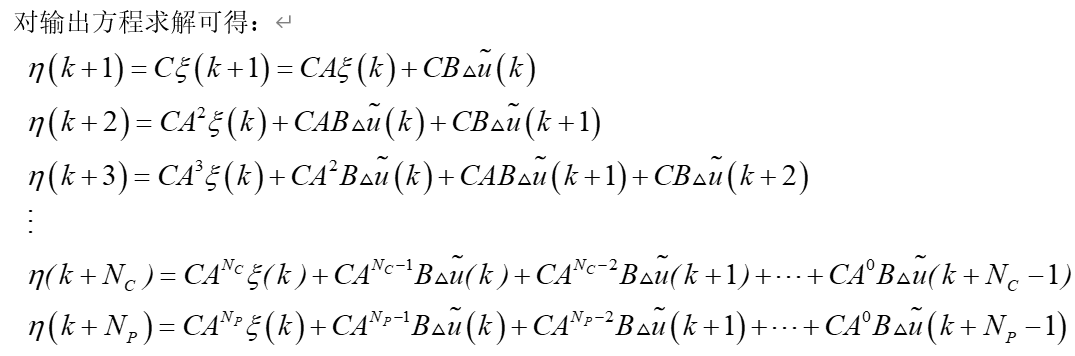
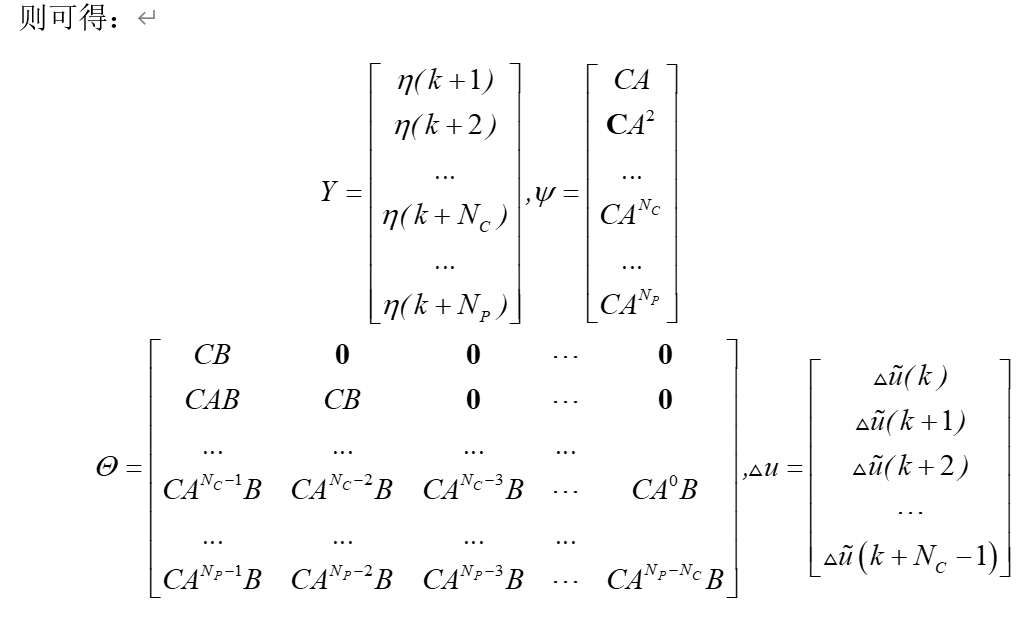
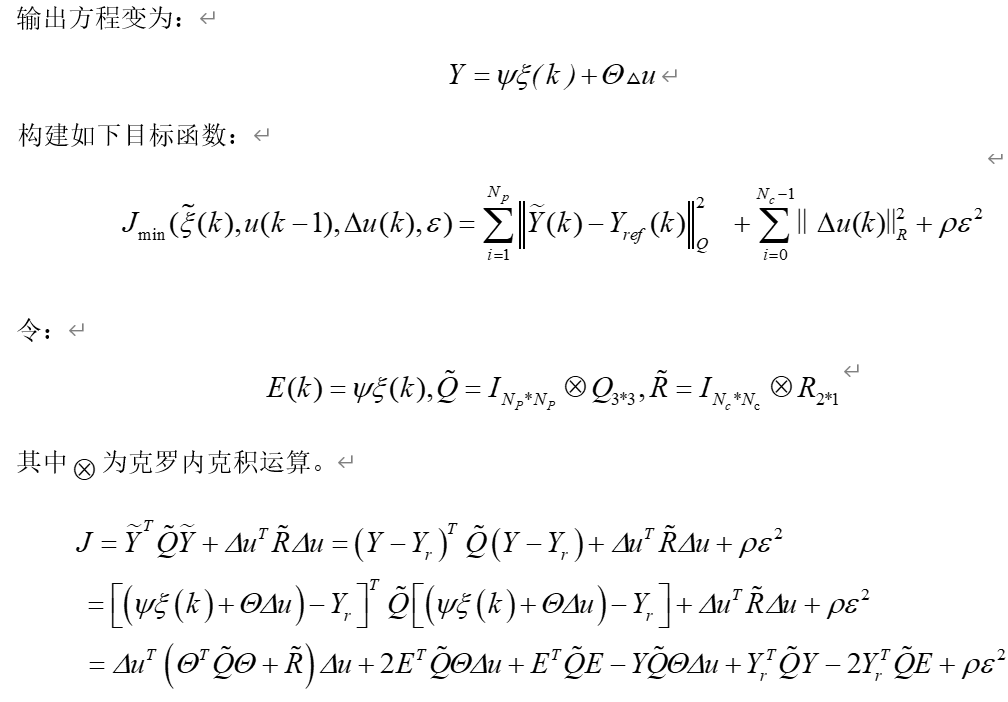



4.仿真结果
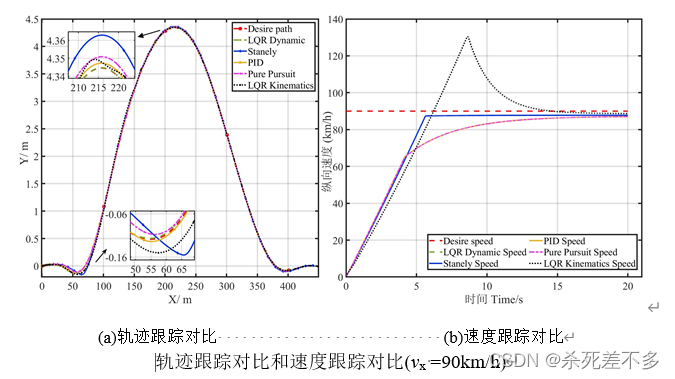
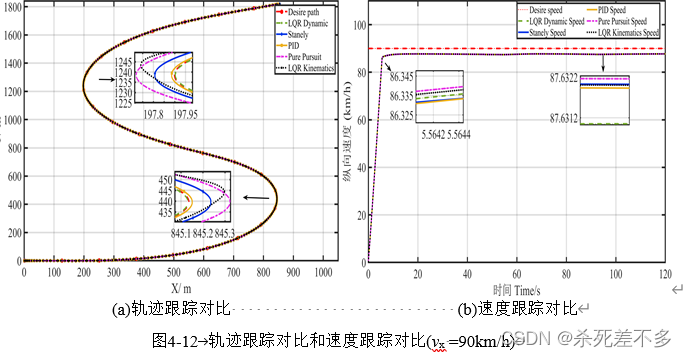
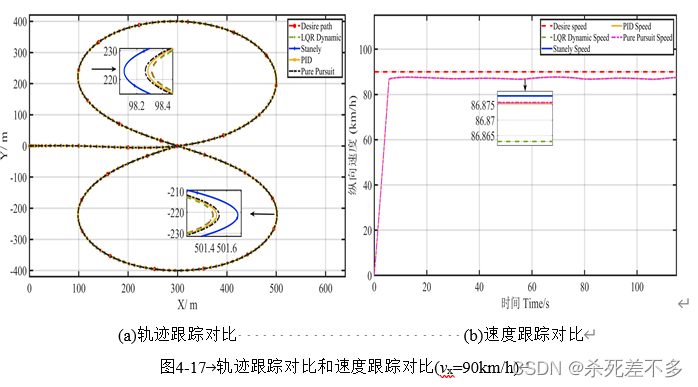
Carsim与Mtatlab仿真链接:
https://download.csdn.net/download/weixin_58477062/89135729(斯坦利)
https://download.csdn.net/download/weixin_58477062/89135728(纯跟踪)
https://download.csdn.net/download/weixin_58477062/88423233(基于预瞄的PID)
参考文献:
- Thrun S, Montemerlo M, Dahlkamp H,et al. Stanley: The Robot that Won the DARPA Grand Challenge[J].Journal of Field Robotics, vol.23 , no.9, pp.661-692, 2016.
- 陈诚.无人驾驶车辆轨迹跟踪控制[J].汽车实用技术,2022,47(22):45-49.




 本文详细探讨了自动驾驶汽车的车辆模型,包括运动学模型、单轨动力学模型和四轮动力学模型,以及离散化方法,如前向欧拉、中点欧拉和双线性变换。重点介绍了斯坦利轨迹跟踪、基于预瞄PID控制、LQR算法等轨迹跟踪算法的应用。文章还提到了仿真工具如Carsim和Matlab的链接。
本文详细探讨了自动驾驶汽车的车辆模型,包括运动学模型、单轨动力学模型和四轮动力学模型,以及离散化方法,如前向欧拉、中点欧拉和双线性变换。重点介绍了斯坦利轨迹跟踪、基于预瞄PID控制、LQR算法等轨迹跟踪算法的应用。文章还提到了仿真工具如Carsim和Matlab的链接。


















 868
868

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








