数值分析期末总结一

一、设有：x为准确值，x为近似值
1、绝对误差：e(x) = x-x
2、相对误差：er(x) = e(x)/|x*|
3、绝对误差限：|e(x) |= | x-x*| <= p(x)

4、已知相对误差，求近似值x几位有效数字

5、

（1）比如：1000/1.5---->改为1/（1.5/1000）
（2）
（3）

二、不动点迭代：
1、不动点x*的定义：

2、解题步骤：
（1）构造出x=…
（2）判断是否收敛：
1）判断 构造出的函数P（x）( 并且 x =P（x) )在定义域[a,b]内，P(x)值域也是在[a,b]内，
2）P(x)的一阶导数P’(x)在定义域[a,b]内的值域是小于等于L（0<L<1）
3）则收敛
例题：

3、收敛阶：
方法：已经求出不动点x*,所以可以求出一阶导P’(x)和P’(x*)的值=0，二阶导P’‘(x)和P’'(x*)的值=0…最后求得某阶导数以及在x=x处，值不等于0，就为收敛剂

例题：四阶收敛级（可以看出x=2）

三、牛顿迭代法
1、迭代公式Xn+1 = Xn - f(Xn)/f’(Xn)

2、解题步骤
（1）确定f(Xn)函数
（2）求出导数f’(Xn)
（3）写出迭代公式Xn+1
（4）迭代初值X0简单取（最好整数1，2…）

3、简单迭代法三种改进

重根适合后面两种，例题：

四、雅可比迭代法
1、
第一个式子：除了X1以外的全部移到等式右边，然后左右两边除以X1的系数
第二个式子：除了X2以外的全部移到等式右边，然后左右两边除以X2的系数
后面类似…

然后进行左右迭代：
左边都X的为k+1次，右边都为X的k次

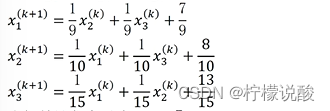
然后对所有的变量取初值为0，可得后面不同次的迭代结果

五、高斯-赛德迭代（Guss-side）
1、第一步与雅可比迭代法一样，把X1、X2、X3、移到等号右边

2、第二步得到迭代形式如下：
把上一次迭代结果带入下一次需要迭代的参数里面

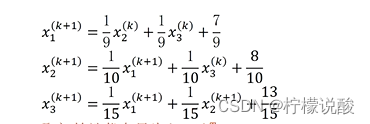
3、然后对所有的变量取初值为0，可得后面不同次的迭代结果
（第三步与雅可比迭代法一样）