【机器学习理论到实践】神经网络推导和代码实现

神经网络是深度学习的基础，最重要的就是熟悉里面的前向传播和反向传播。本文首先从理论切入，首先讲了前向传播，对于反向传播部分，分为了两个部分分别是简单模型（两层）和扩展模型（多层），原理之后是代码部分。
有错误的地方欢迎指出~

1.原理

神经网络是机器学习里面非常重要的模型，下面就讲一讲具体的原理。
下面是参考博客：

1. CSND，推导有点抽象，反向传播有数字例子，比较详细，就是看起来有点累，都是图片
2. 博客园，推导比较详细

最简单的神经网络由三层组成，分别对应输入层、隐藏层、输出层，最主要的训练过程包含两个概念，分别是前向传播和反向传播，下面分别叙述。

1.1前向传播

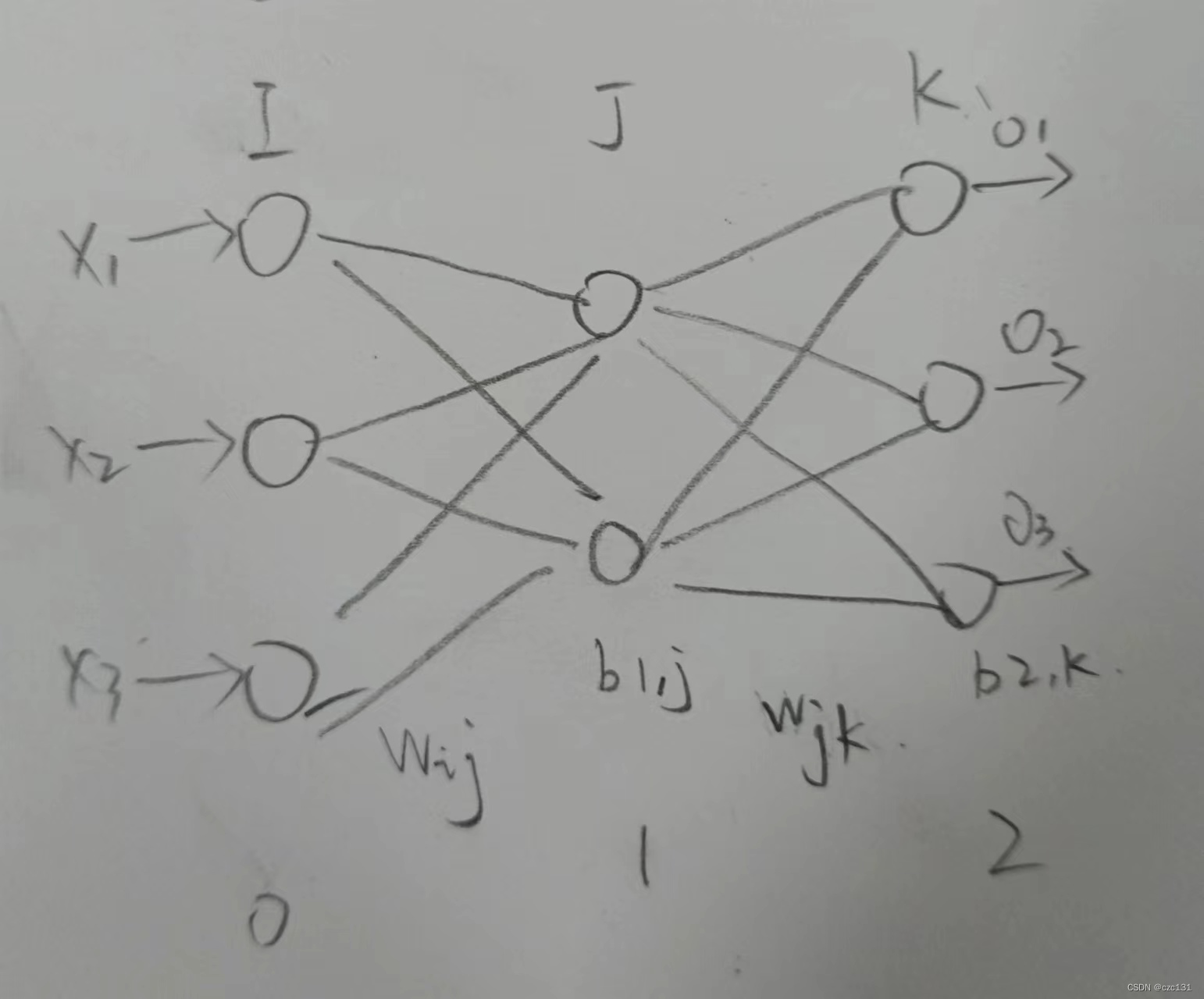假设存在这样一个神经网络，共有三层架构，分别对应了输入层（0）、隐藏层（1）和输出层（2），输入层对应的其实就是输入的维度，这里假设输入的是$I\times 1$矩阵，隐藏层有$J$个神经元，输出维度为$K\times 1$。之所以下标从0开始，是因为这里的第一层就是单纯的输入，没有经过处理，我觉得不应该作为第一层（ 其实毫无根据 ）。

前向传播顾名思义就是向前传播，这里的前就是输入到输出。对于非输入层的神经元，这里就以这里的输入层（0）和隐藏层（1）为例，设两层之间的所有神经元都建立一个连接，系数记为$w_{ij},i=1,...I,j=1,2,...,J$，第$1$层第$j$个神经元的输出记为$O_{1,j}$，第一层每个神经元对应一个偏置$b_{1,j}$。对于每一个隐藏层（1）的神经元，其输出$O_{1,j}$如下：
$$\begin{gathered} O_{1,j}=g(N(O_0)) \\ N(O_0)=\sum _{i=1}^I{w}_{ij}{O}_{0,i}+b_{1,j} \end{gathered}$$其实$N(O_0)$就是对连接到第$j$个点的所有神经元的输出$O_{0,i}$（也就是输入$x$）进行加权求和。如图，每个隐藏层（1）的神经元都和输入层（0）的所有神经元有一个连接系数$w_{ij}$，将所有输入值加权求和(${\sum }_{i=1}^I{w}_{ij}{O}_{0,i}+b_{1,j}$)，激活后就得到了隐藏层的输出。
$g(x)$为激活函数，常用的有$tanh、sigmoid$等函数，这里就以$sigmoid$函数为例，记为$\sigma$，表达式如下：$$\sigma (x)=\frac{1}{1+e^{-x}}$$这个函数有一个比较好的性质，也就是求导的值${\sigma }^{\prime }(x)$可以由求导前的函数值$\sigma (x)$表示：
$$\begin{gathered} {\sigma }^{\prime }(x)=\frac{e^x}{(1+e^{-x}{)}^2} \\ =\frac{1+e^{-x}-1}{(1+e^{-x}{)}^2} \\ =\frac{1}{1+e^{-x}}-\frac{1}{(1+e^{-x}{)}^2} \\ =\frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}}) \\ =\sigma (x)(1-\sigma (x)) \end{gathered}$$这使得对于$\sigma (x)$的求导变得非常简单。
对于隐藏层和输出层，其实和前面说的输入层和隐藏层类似，不同之处就是把输入换成了隐藏层的输出。
(具体的例子)

1.2.反向传播

下面是相对复杂的反向传播部分。正向传播就是基于所有的权重计算出相应的输出，然而一开始不知道正确的权重，那么输出和实际的答案一定是大相径庭，那么如何对照答案来更新参数，最主流的做法就是利用反向传播。

1.2.1.基本模型

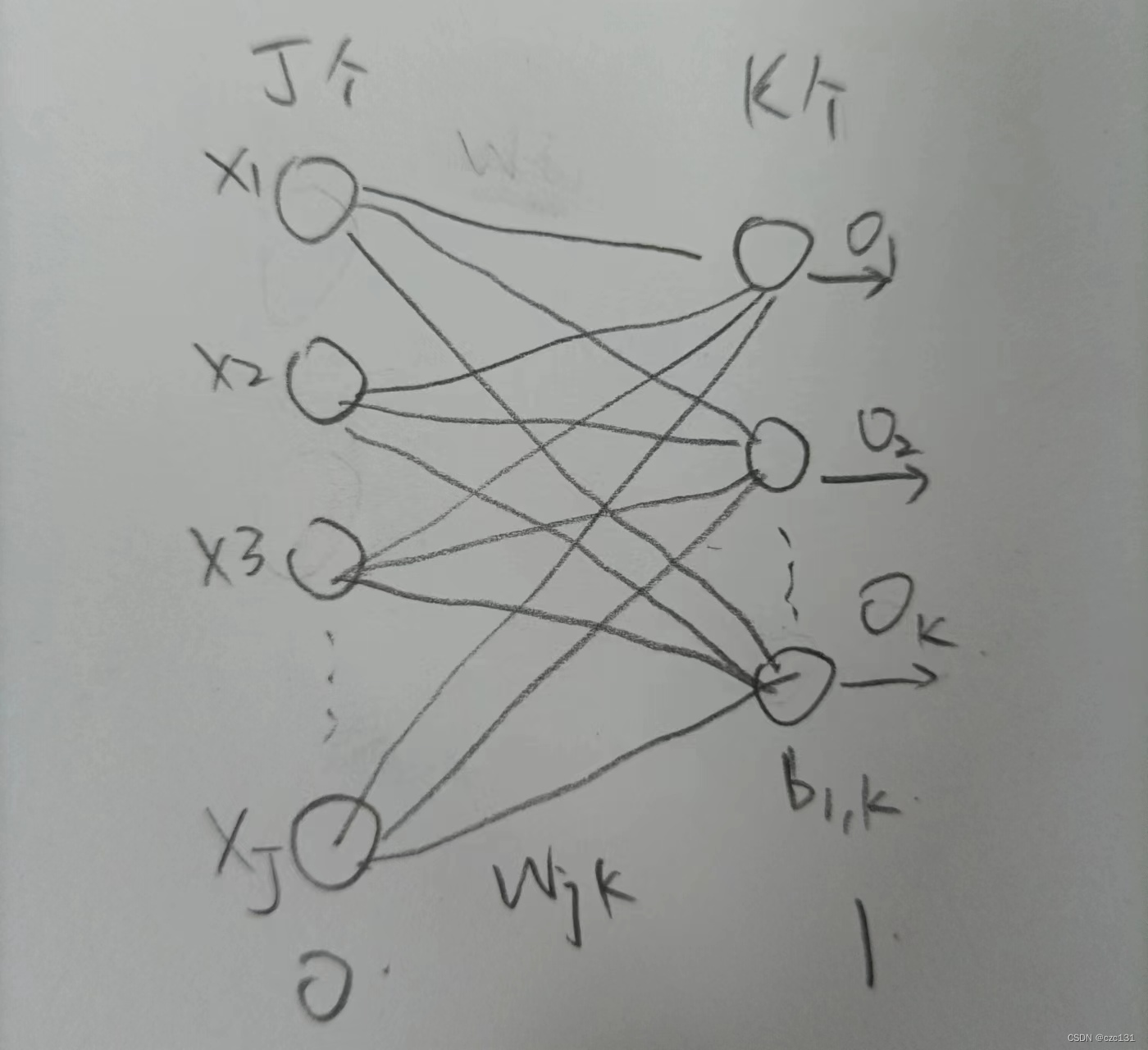简单起见，先看一个最简单的网络，这是一个两层的网络，分别对应0、1层。

输入层（0）有$J$个神经元，输出层（1）有$K$个神经元，直接对应了输入和输出的维度，每个输入和输出之间有一个系数$w_{jk}$连接，第1层有偏置，第$k$个偏置记为$b_{1,k}$。
这里引入损失函数的概念，所有的优化问题最后会归结为一个式子，记为$L(output,label)$，这个函数由输出（$output$）和目标输出（$label$）计算出一个值，这个值指明了优化的方向，一般来说这个值越小越好。
在这里，我们希望的是输出和目标输出越接近越好，记：
$$L(output,label)=\frac{1}{2}\sum _{k=1}^K(outpu{t}_k-labe{l}_k{)}^2$$也就是这个值越小越好。
为了更新系数$w_{jk}$和偏置$b_{1,k}$，一般基于梯度下降，本质是求偏导，表达式记为：
$$\begin{gathered} w_{jk}=w_{jk}-{\alpha }_w\frac{\partial L}{\partial w_{jk}} \\ {b}_{1,k}=b_{1,k}-{\alpha }_b\frac{\partial L}{\partial b_{1,k}} \end{gathered}$$
首先简单梳理一下从输入$X=O_{0,j}$到计算得到损失$L$的过程，首先输入$X$，经过以下变换：

1. 线性求和(N)，$N={\sum }_{j=1}^J{w}_{jk}{O}_{0,j}+b_{1,k}$
2. 激活(O)，$O=\sigma (N)$
3. 计算损失(L)，$L=L(O,label)$

不难看出，$L$是一个关于$w_{jk}$的复合函数，此时的求导需要用到链式求导法则，链式求导简单说就是逐层求导，定义如下：
$$\frac{\partial g(f(x))}{\partial x}=\frac{\partial f}{\partial x}\frac{\partial L}{\partial f}$$利用链式求导写出求解$w_{ij}$和$b_{1,k}$的表达式：
$$\begin{gathered} \frac{\partial L}{\partial w_{jk}}=\frac{\partial N_{1,k}}{\partial w_{jk}}\frac{\partial O_{1,k}}{\partial N_{1,k}}\frac{\partial L}{\partial O_{1,k}} \\ \frac{\partial L}{\partial b_{1,k}}=\frac{\partial N_{1,k}}{\partial b_{1,k}}\frac{\partial O_{1,k}}{\partial N_{1,k}}\frac{\partial L}{\partial O_{1,k}} \end{gathered}$$下面先讲$w_{jk}$，$b_{1,k}$要更简单，本质是一样的。
逐个求解，首先是对于$\frac{\partial L}{\partial O_{1,k}}$，这个也就是损失函数对于输出求导：
$$L(O,label)=\frac{1}{2}\sum _{k=1}^K(O_{1,k}-labe{l}_k{)}^2$$这里的$label$就是给定预期目标（标签），因为不会改变，相当于常数，可得：
$$\frac{\partial L}{\partial O_{1,k}}=O_{1,k}-labe{l}_k$$因为只有一个神经元$w_{jk}$建立连接，所以求和符号消除了。
下面求解$\frac{\partial O_{1,k}}{\partial N_{1,k}}$，写出表达式：
$$O_{1,k}=\sigma (N_{1,k})$$对这个式子求导可以得到（根据前面提到的$\sigma (x)$求导规则）：
$$\frac{\partial O_{1,k}}{\partial N_{1,k}}=O_{1,k}(1-O_{1,k})$$这主要是基于${\sigma }^{\prime }(x)=\sigma (x)(1-\sigma (x))$，这一层的输出是$O_{1,k}$，因此导数也可以表达为输出的形式。
最后是$\frac{\partial N_{1,k}}{\partial w_{jk}}$，还是先写出表达式：
$$N_{1,k}=\sum _{j=1}^J{w}_{jk}{O}_{0,j}+b_1$$这里其实和只有一条神经元连接（因为只考虑一个连接系数$w_{jk}$），不难看出：
$$\frac{\partial N_{1,k}}{\partial w_{jk}}=O_{0,j}$$而$O_{0,j}$表示第0层的第$j$个点的输出，这其实就是第$j$个输入值$x_j$。
汇总得到下式：
$$\frac{\partial L}{\partial w_{jk}}=O_{0,j}{O}_{1,k}(1-O_{1,k})(O_{1,k}-labe{l}_k)$$
对于$b_{1,k}$，唯一不同的只有$\frac{\partial N_{1,k}}{\partial b_{1,k}}$，因为$\frac{\partial N_{1,k}}{\partial b_{1,k}}=1$，所以：
$$\frac{\partial L}{\partial b_{1,k}}=O_{1,k}(1-O_{1,k})(O_{1,k}-labe{l}_k)$$记：
$${\delta }_{1,k}=\frac{\partial O_{1,k}}{\partial N_{1,k}}\frac{\partial L}{\partial O_{1,k}}=O_{1,k}(1-O_{1,k})(O_{1,k}-labe{l}_k)$$这个值也就是第1层第$k$个神经元的损失，此时$w_{jk}$和$b_{1,k}$的表达式可简化为：
$$\begin{gathered} \frac{\partial L}{\partial w_{jk}}=O_{0,j}{\delta }_{1,k} \\ \frac{\partial L}{\partial b_{1,k}}={\delta }_{1,k} \end{gathered}$$到此，两层神经网络结束。

1.2.2.扩展模型

下面将扩展到更多层，这就涉及到更长的链式求导，先考虑稍微复杂的三层神经网络，再搬出前面的图：

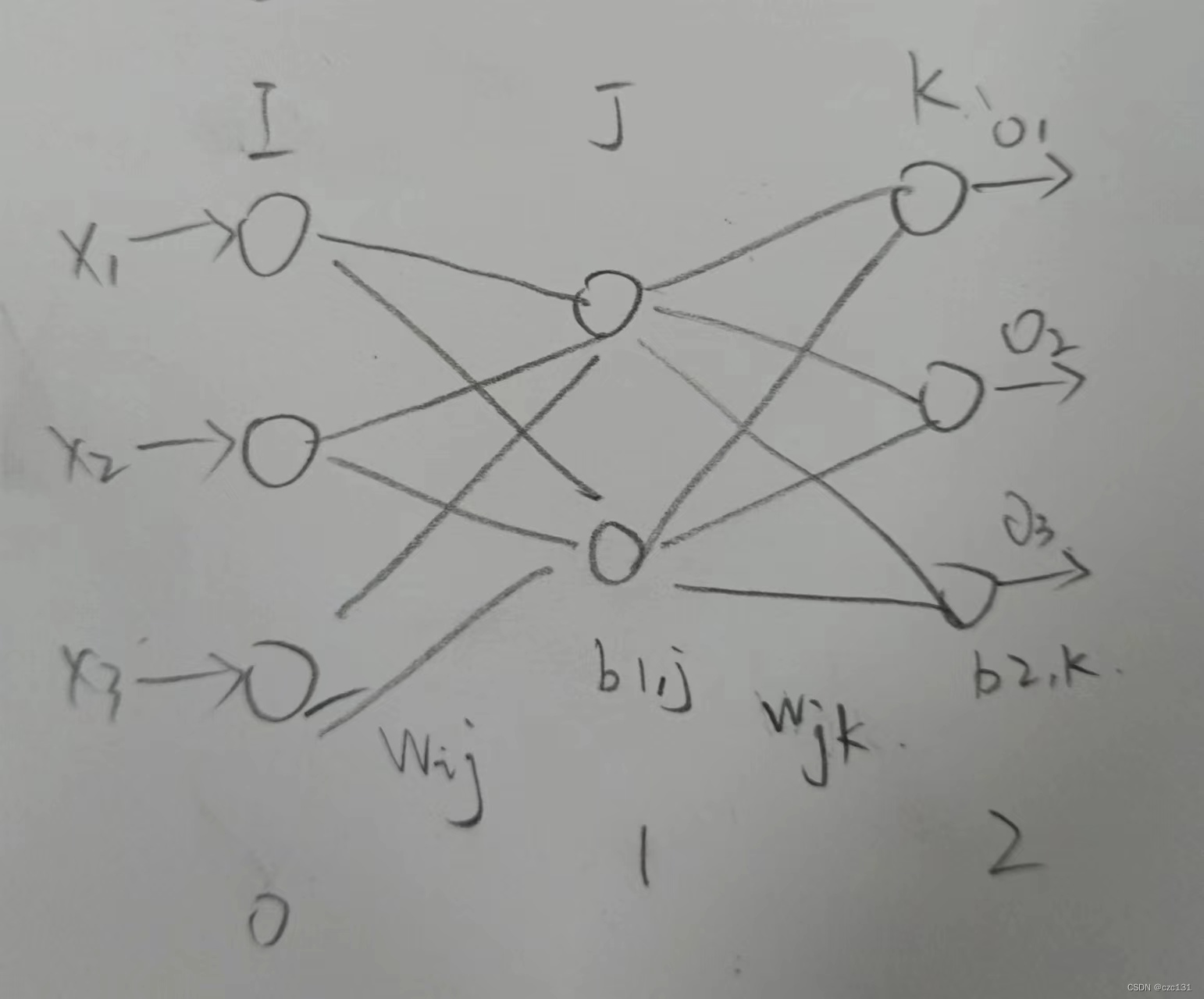
1、2层之间的$w_{jk}$和$b_{2,k}$的更新和两层模型意思是一样的，不同的在于0、1层之间的$w_{ij}$和$b_{1,j}$的更新。
在三层模型中，对于0、1层之间的系数$w_{ij}，$其连接第0层某个神经元和第1层的某个神经元，然后所有第1层的神经元与所有第2层的神经元相连，因此这个系数影响第1层的某个神经元，影响第2层的所有神经元。
这个过程和两层结构类似：第0层的的神经元输出经过加权累加到了第1层进行激活，激活后的输出再加权求和到第2层激活，最后输出。不同于前面两层结构的就是多了一层加权求和再激活的过程，后面的操作和前面的是一致的，写出表达式：
$$\begin{gathered} \frac{\partial L}{\partial w_{ij}}=\frac{\partial N_{1,j}}{\partial w_{ij}}\frac{\partial O_{1,j}}{\partial N_{1,j}}\sum _{k=1}^K\frac{\partial N_{2,k}}{\partial O_{1,j}}\frac{\partial O_{2,k}}{\partial N_{2,k}}\frac{\partial L}{\partial O_{2,k}} \\ \frac{\partial L}{\partial b_{1,j}}=\frac{\partial N_{1,j}}{\partial b_{1,j}}\frac{\partial O_{1,j}}{\partial N_{1,j}}\sum _{k=1}^K\frac{\partial N_{2,k}}{\partial O_{1,j}}\frac{\partial O_{2,k}}{\partial N_{2,k}}\frac{\partial L}{\partial O_{2,k}} \end{gathered}$$这里多了${\sum }_{k=1}^K$是因为$w_{ij}$连接的$j$节点在后面与所有点$K$个节点建立了连接（影响了后面的所有），因此要累加所有$k$个节点的偏导。
后面两项的计算和前面类似，简单说就是第2层第$k$个神经元的损失${\delta }_{2,k}$，如下：
$$\begin{gathered} \frac{\partial O_{2,k}}{\partial N_{2,k}}\frac{\partial L}{\partial O_{2,k}}={\delta }_{2,k} \\ =O_{2,k}(1-O_{2,k})(O_{2,k}-labe{l}_k) \end{gathered}$$主要是$\frac{\partial N_{1,j}}{\partial w_{ij}}\frac{\partial O_{1,j}}{\partial N_{1,j}}{\sum }_{k=1}^K\frac{\partial N_{2,k}}{\partial O_{1,j}}$部分。从后往前一个个看，首先是$\frac{\partial N_{2,k}}{\partial O_{1,j}}$，因为$N_{2,k}={\sum }_{j=1}^J{w}_{jk}{O}_{1,j}+b_{2,k}$，实际上和$O_{1,j}$关联的只有$w_{jk}$，可得：
$$\frac{\partial N_{2,k}}{\partial O_{1,j}}=w_{jk}$$对于$\frac{\partial O_{1,j}}{\partial N_{1,j}}$，这其实就是第1层输出激活求导，表达式如$O_{1,j}=\sigma (N_{1,j})$，可得：
$$\frac{\partial O_{1,j}}{\partial N_{1,j}}=O_{1,j}(1-O_{1,j})$$$N_{1,j}$关于$w_{ij}$的表达式为$N_{1,j}={\sum }_{i=1}^I{w}_{ij}{O}_{0,i}+b_{1,j}$，因此：
$$\begin{gathered} \frac{\partial N_{1,j}}{\partial w_{ij}}=O_{0,i} \\ \frac{\partial N_{1,j}}{\partial b_{1,j}}=1 \end{gathered}$$那么可以写出最终的结果：
$$\begin{gathered} \frac{\partial L}{\partial w_{ij}}=O_{0,i}{O}_{1,j}(1-O_{1,j})\sum _{k=1}^K{w}_{jk}{\delta }_{2,k} \\ \frac{\partial L}{\partial b_{1,j}}=O_{1,j}(1-O_{1,j})\sum _{k=1}^K{w}_{jk}{\delta }_{2,k} \end{gathered}$$观察后边的${\sum }_{k=1}^K{w}_{jk}{\delta }_{2,k}$，$w_{jk}$分别连接的是1、2层的第$j,k$个神经元，而${\delta }_{2,k}$是第二层的第$k$个神经元的损失，这其实是对损失加权求和。类似前面的定义，定义${\delta }_{1,j}=O_{1,j}(1-O_{1,j}){\sum }_{k=1}^K{w}_{jk}{\delta }_{2,k}$，也就是第1层第$j$个神经元的损失，简化后的式子如：
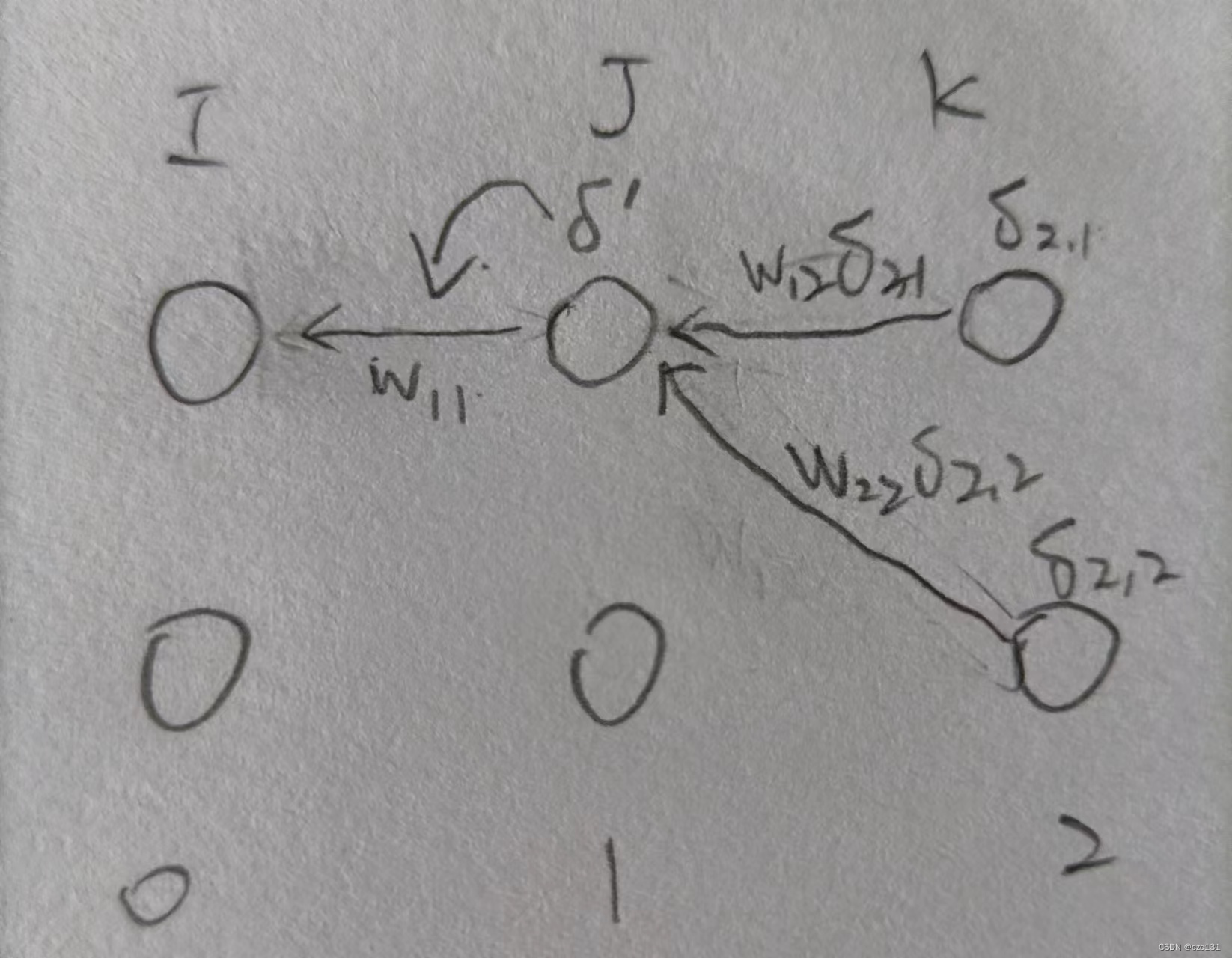
$$\begin{gathered} \frac{\partial L}{\partial w_{ij}}=O_{0,i}{\delta }_{1,j} \\ \frac{\partial L}{\partial b_{1,j}}={\delta }_{1,j} \end{gathered}$$总结一下，反向传播实际上是一个收集误差的过程。如图，对于第1层第一个神经元，其会分别以$w_{11}$和$w_{22}$的权值影响到第2层的第一个和第二个神经元，那么在反向传播的时候，在算出第2层第一个和第二个神经元的误差${\delta }_{2,1},{\delta }_{2,2}$后，其又会以加权求和的方式回到第1层第一个神经元，乘上激活函数求导得到的结果成为第1层第1个神经元的损失${\delta }_{1,1}$，进一步影响连接到连接该点的系数$w_{11}$。

扩展到更多层，本质上是在做同一件事，对于一个$n$层网络，要算两层之间的系数$w$和相关的$b$，都可以抽象为三层架构（下一层不是输出层）和两层架构（下一层就是输出层）的第0层和第1层。假设要更新的是位于$Layer-1$和$Layer$之间的系数$w_{ij}$和第$Layer$层的系数$b_{Layer,j}$，可以写为：
$$\begin{gathered} \frac{\partial L}{\partial w_{ij}}=O_{Layer-1,i}{\delta }_{Layer,j} \\ \frac{\partial L}{\partial b_{Layer,j}}={\delta }_{Layer,j} \end{gathered}$$其中：
$${\delta }_{Layer,j}=\{\begin{array}{c}{O}_{Layer,j}(1-O_{Layer,j}){\sum }_{k=1}^K{w}_{jk}{\delta }_{Layer+1,k},Layer不为输出\\ O_{Layer,j}(1-O_{Layer,j})(O_{Layer,j}-labe{l}_k),Layer为输出\end{array}$$
当然，不同的激活函数，前面的$O_{Layer,j}(1-O_{Layer,j})$是会变的。
到这里，多层神经网络的原理就算结束了。

2.代码

下面尝试用代码实现一个多层神经网络，使用的是一个关于糖尿病的数据集，其中输入是10维数据，输出是1维数据，我写的代码是可变层数和可变隐藏层大小的，但是隐藏层的大小必须一致。
一开始调试发现输出总是一样，后来发现是迭代轮数太少了…直接设置了比较大的学习率（5）和3000轮迭代，但是尽管如此最终的拟合有优度还是只能到0.7左右，可能是数据集太抽象了？或者应该分批次处理，一个个迭代更新感觉是没法得到很理想的结果。
（也有可能代码错了？最好不是…）
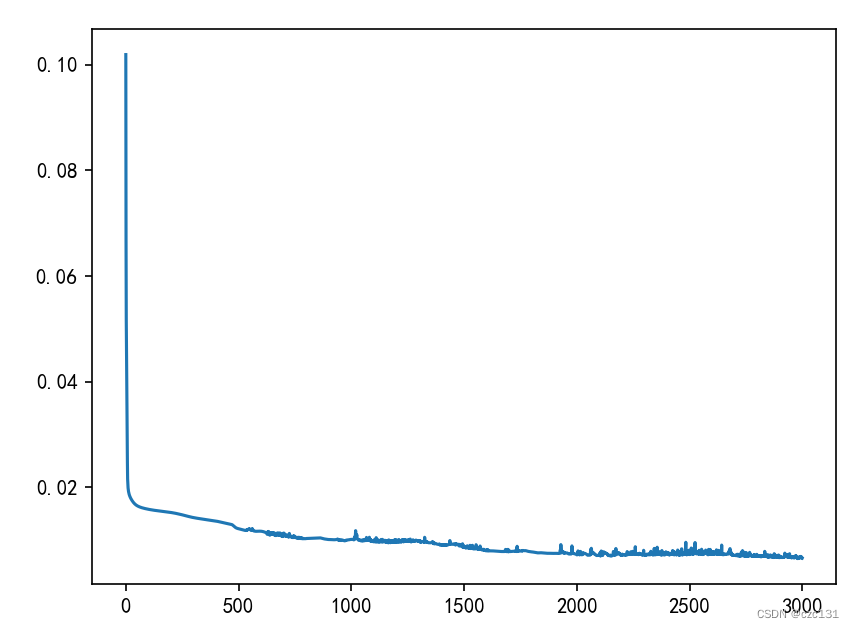
我设置了2层隐藏层，每层大小是10，下面是loss曲线，一共3000轮，还有下降的趋势，但是这样来看收敛实在太慢了。

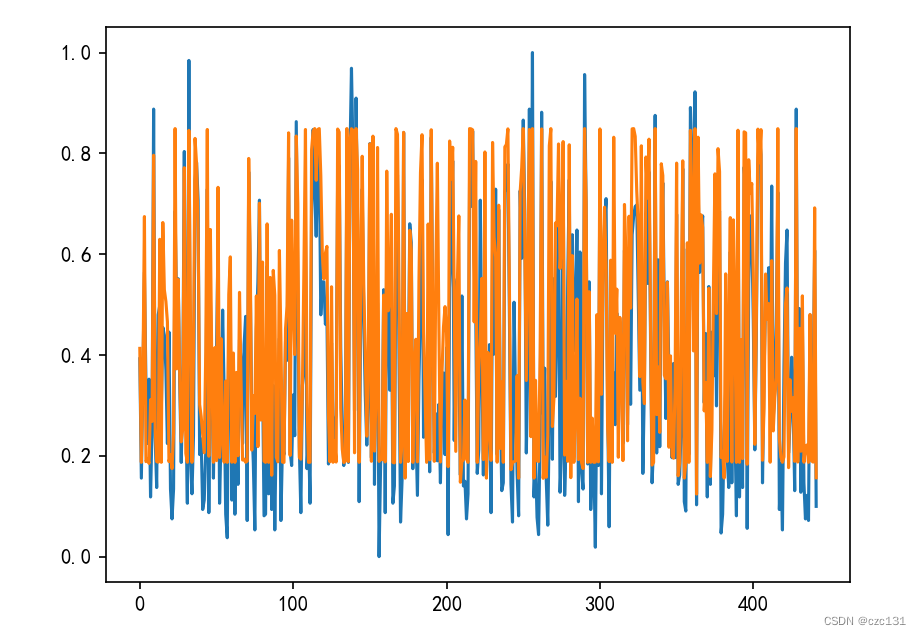
下面是拟合结果和实际结果的对比，还是有靠近的趋势的，就是可能确实是太抽象了，没法拟合的太好。

下面贴出完整代码：

# 复现神经网络
import time

import numpy as np
from matplotlib import pyplot as plt
from numpy import dot
from numpy.linalg import inv
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.preprocessing import MinMaxScaler
from numpy.random import uniform

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 糖尿病数据集
from sklearn.datasets import load_diabetes


def load_data():
    diabetes = load_diabetes()
    X = diabetes.data  # data
    y = diabetes.target  # label
    # 对所有数据按列归一化
    scalar = MinMaxScaler()
    for i in range(X.shape[1]):
        X[:, i] = scalar.fit_transform(X[:, i].reshape(-1, 1)).reshape(-1)
    # print(len(y.shape),y.shape)
    if len(y.shape) == 1:
        y = y.reshape(-1, 1)
    for i in range(y.shape[1]):
        y[:, i] = scalar.fit_transform(y[:, i].reshape(-1, 1)).reshape(-1)
    # print(X[:5])
    # print(y[:5])
    return X, y


class MyNet():
    # sigmoid
    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    # 损失函数
    def loss_func(self, output, label):  # 输入是列向量
        return 1 / 2 * (output - label).T @ (output - label)

    def fit(self, X, Y, epochs, alpha=0.01, layers=2, layer_size=3):  # 中间的隐藏层层数和隐藏层的大小
        if layers < 1:
            assert "隐藏层至少为1,当前layers=%d" % (layers)
        if len(Y.shape) == 1:  # 一维
            Y = Y.reshape(-1, 1)
        in_features = X.shape[1]
        out_features = Y.shape[1]
        samples = X.shape[0]
        print('in_features:', in_features)
        print('out_features:', out_features)
        print('samples:', samples)
        # 矩阵初始化(随机初始化)
        w_first = uniform(0,1,(in_features,layer_size)) # 每一行是一个输入神经元对所有下一层神经元的权值
        w_last = uniform(0,1,(layer_size,out_features)) # 每一行是一个输入神经元对所有下一层神经元的权值
        self.w=None # 防止后续报错
        if layer_size > 1: # 刚好等于1就不需要了
            w = uniform(0,1,(layers-1,layer_size,layer_size))
        b_last = uniform(0,1,(out_features, 1)) # # 每一列是一层的系数b
        b = uniform(0,1,(layers,layer_size,1)) # 隐藏层的

        # 运行过程中的变量
        delta = np.zeros((layers, layer_size, 1), dtype=float)
        delta_last = np.zeros((out_features, 1), dtype=float)  # 每一列是一层的δ
        out_last = np.zeros((out_features, 1), dtype=float)  # 每一列是一层的output
        out = np.zeros((layers, layer_size, 1), dtype=float)
        # 开始迭代
        loss_list = []
        for epoch in range(epochs):
            loss = 0
            for idx in range(samples):
                x = X[idx].reshape(-1, 1)
                y = Y[idx].reshape(-1, 1)
                # 前向传播
                for layer in range(layers + 1):  # 0其实就对应了0和1层的w和1层的偏置
                    if layer == 0:  # 第一层
                        out[layer] = self.sigmoid(w_first.T @ x + b[layer])
                    elif layer < layers:  # 不是最后一层
                        # print('w[%d]'%(layer-1))
                        out[layer] = self.sigmoid(w[layer - 1].T @ out[layer - 1] + b[layer])
                    else:  # 最后一层
                        out_last = self.sigmoid(w_last.T @ out[layer - 1] + b_last)
                # 反向传播
                for layer in range(layers, -1, -1):  # layers,...,0
                    # 计算出每一层的损失
                    if layer == layers:  # 最后一层(输出层)
                        # print('输出层')
                        delta_last = out_last * (1 - out_last) * (out_last - y)  # 最后一层隐藏层
                    elif layer == layers - 1:  # 隐藏层最后一层,连接输出层
                        # print('最后一层隐藏')
                        delta[layer] = out[layer] * (1 - out[layer]) * (w_last @ delta_last)
                    else:  # 最后一层
                        # print('隐藏')
                        delta[layer] = out[layer] * (1 - out[layer]) * (w[layer] @ delta[layer + 1])
                # 更新系数
                for layer in range(layers + 1):
                    # print(layer)
                    if layer == 0:  # 输入-隐藏
                        # print('输入-隐藏')
                        det_w = x @ delta[layer].T
                        w_first = w_first - alpha * det_w  # # O_{Layer-1,i}δ_{Layer,j}
                        b[layer] = b[layer] - alpha * delta[layer]  # δ_{Layer,j}
                    elif layer < layers:  # 隐藏-隐藏
                        # print('隐藏-隐藏')
                        det_w = out[layer - 1] @ delta[layer].T
                        w[layer - 1] = w[layer - 1] - alpha * det_w
                        b[layer] = b[layer] - alpha * delta[layer]
                    else:  # 隐藏-输出
                        # print('隐藏-输出')
                        det_w = out[layer - 1] @ delta_last.T
                        w_last = w_last - alpha * det_w
                        b_last = b_last - alpha * delta_last
                this_loss = self.loss_func(out_last, y)
                # print('this_loss',this_loss,' out=',out_last,' y=',y)
                loss += this_loss
            loss_list.append(loss[0][0]/samples)
            print('epoch %d loss:%.6f' % (epoch + 1, loss / samples))
        plt.plot(loss_list)
        plt.show()
        # 保存参数
        self.w_first = w_first
        self.w_last = w_last
        self.w = w
        self.b_last = b_last
        self.b = b
        self.in_features = in_features
        self.out_features = out_features
        self.layers = layers
        self.layer_size = layer_size

    def predict(self, X):
        in_features = self.in_features
        if X.shape[1] != in_features:
            assert "输入维度不正确,应为%d×1" % in_features
        w_first = self.w_first
        w_last = self.w_last
        w = self.w
        b_last = self.b_last
        b = self.b
        layers = self.layers
        out_features = self.out_features
        layer_size = self.layer_size
        samples = X.shape[0]  # 数量
        ans = np.zeros((samples, out_features))
        out_last = np.zeros((out_features, 1), dtype=float)  # 每一列是一层的output
        out = np.zeros((layers, layer_size, 1), dtype=float)
        for i in range(samples):
            x = X[i].reshape(-1, 1)
            # 前向传播
            for layer in range(layers + 1):  # 0其实就对应了0和1层的w和1层的偏置
                if layer == 0:  # 第一层
                    out[layer] = self.sigmoid(w_first.T @ x + b[layer])
                elif layer < layers:  # 不是最后一层
                    out[layer] = self.sigmoid(w[layer - 1].T @ out[layer - 1] + b[layer])
                else:  # 最后一层
                    out_last = self.sigmoid(w_last.T @ out[layer - 1] + b_last)
            ans[i] = out_last.reshape(-1)
        return ans


if __name__ == '__main__':
    X, y = load_data()  # 获取归一化后的数据

    myNet = MyNet()
    myNet.fit(X, y, epochs=3000, alpha=5, layers=2, layer_size=10) 
    pred=myNet.predict(X)
    for i in range(y.shape[0]):
        print('true=',y[i],'pred=',pred[i])
    print('r^2=%.2f'%(r2_score(y,pred)))
    plt.plot(y[:,0])
    plt.plot(pred[:,0])
    plt.show()

总的来说，简单的神经网络就是这样，但是神经网络实际上有很多种，花样百出，先浅入个门好了。