NumPy矩阵行列式计算与可视化

Just You786

于 2025-10-11 01:11:23 发布

阅读量523

点赞数 21

CC 4.0 BY-SA版权

文章标签： python numpy 矩阵新人首发

本文链接：https://blog.csdn.net/weixin_61280505/article/details/152970250

#【投稿赢 iPhone 17】「我的第一个开源项目」故事征集：用代码换C位出道！#

一、作业背景与目标

在 “数据分析与可视化” 课程 “矩阵运算与相关操作” 章节中，本次作业核心是借助 NumPy 库完成矩阵行列式计算，再通过 Matplotlib 对矩阵及计算结果进行可视化，以此验证行列式计算的准确性，且直观呈现 “矩阵元素变化对行列式的影响”。

二、实现工具与核心思路

1. 用到的 Python 库

NumPy：负责矩阵的定义与行列式计算。NumPy 的linalg.det()函数可高效计算方阵的行列式，同时支持多维数组的便捷操作；

Matplotlib：负责矩阵结构与计算结果的可视化。通过绘制矩阵网格、填充元素文本，让抽象的矩阵 “可视化”，再单独展示行列式值，让结果更直观。

2. 核心实现思路

矩阵合法性校验：先判断输入矩阵是否为方阵（只有方阵才有行列式），避免计算报错；
行列式计算：调用np.linalg.det()计算行列式，处理浮点运算精度问题；
可视化设计：分两部分展示 —— 左侧绘制矩阵网格与元素，右侧显示行列式结果；
多案例演示：用 2×2 矩阵、3×3 矩阵（含线性相关与无关案例）、自定义矩阵验证功能，观察元素变化对行列式的影响。

三、完整代码与逐段解析

第一部分：库导入与中文显示配置

import numpy as np
import matplotlib.pyplot as plt

# 设置中文显示（简化字体配置，避免因字体缺失导致报错）
plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei"]  # 优先使用系统常见中文字体
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

功能说明：导入numpy（矩阵计算核心库）和matplotlib.pyplot（可视化库），并配置中文字体显示参数，确保可视化结果中的中文和负号正常显示，避免乱码。

第二部分：行列式计算函数

def calculate_determinant(matrix):
    """计算矩阵的行列式"""
    try:
        # 检查是否为方阵
        if matrix.shape[0] != matrix.shape[1]:
            raise ValueError("只有方阵才有行列式")

        # 计算行列式
        det = np.linalg.det(matrix)
        return det
    except Exception as e:
        print(f"计算行列式时出错: {e}")
        return None

功能说明：定义calculate_determinant函数，负责行列式计算的核心逻辑。先校验矩阵是否为方阵（非方阵无行列式），再调用numpy的linalg.det函数计算行列式值，通过try-except捕获异常并提示错误，保证计算稳定性。

第三部分：矩阵与结果可视化函数

def visualize_matrix_and_result(matrix, determinant,title):
    """可视化矩阵及其行列式结果"""
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
    fig.suptitle("矩阵及其行列式计算结果", fontsize=16)

    # 可视化矩阵
    n = matrix.shape[0]
    ax1.set_title(title)
    ax1.axis('off')

    # 绘制矩阵边框
    cell_size = 1.0
    for i in range(n + 1):
        ax1.plot([0, n * cell_size], [i * cell_size, i * cell_size], 'k-')
        ax1.plot([i * cell_size, i * cell_size], [0, n * cell_size], 'k-')

    # 填充矩阵元素
    for i in range(n):
        for j in range(n):
            ax1.text(j * cell_size + cell_size / 2,
                     n * cell_size - i * cell_size - cell_size / 2,
                     f"{matrix[i, j]}",
                     ha='center', va='center', fontsize=12)

    # 显示行列式结果
    ax2.axis('off')
    result_text = f"该矩阵的行列式值为:\n{determinant:.4f}"
    ax2.text(0.5, 0.5, result_text, ha='center', va='center', fontsize=16)

    plt.tight_layout()
    plt.show()

功能说明：定义visualize_matrix_and_result函数，将矩阵结构和行列式结果可视化。左侧子图绘制矩阵网格并填充元素（元素排列符合数学书写习惯），右侧子图用大字体显示行列式值，通过 “1 行 2 列” 布局清晰呈现计算结果。

第四部分：主函数与案例演示

def main():
    # 示例1: 2x2矩阵
    print("示例1: 2x2矩阵")
    matrix2 = np.array([[4, 7], [2, 6]])
    det2 = calculate_determinant(matrix2)
    print(f"2x2矩阵:\n{matrix2}")
    print(f"行列式值: {det2:.4f}\n")
    visualize_matrix_and_result(matrix2, det2, "2x2矩阵")

    # 示例2: 3x3矩阵
    print("示例2: 3x3矩阵")
    matrix3 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
    det3 = calculate_determinant(matrix3)
    print(f"3x3矩阵:\n{matrix3}")
    print(f"行列式值: {det3:.4f}\n")
    visualize_matrix_and_result(matrix3, det3, "3x3矩阵")

    # 示例3: 自定义矩阵
    print("示例3: 自定义3x3矩阵")
    matrix_custom = np.array([[2, 3, 1], [4, 1, 2], [3, 5, 2]])
    det_custom = calculate_determinant(matrix_custom)
    print(f"自定义3x3矩阵:\n{matrix_custom}")
    print(f"行列式值: {det_custom:.4f}")
    visualize_matrix_and_result(matrix_custom, det_custom, "自定义3x3矩阵")


if __name__ == "__main__":
    main()

功能说明：定义main函数作为程序入口，通过 3 个案例（2x2 矩阵、3x3 线性相关矩阵、自定义 3x3 矩阵）演示完整流程：定义矩阵→调用计算函数→打印结果→调用可视化函数。最后通过if __name__ == "__main__": main()确保脚本直接运行时执行案例演示，符合 Python 模块化设计规范。

四、演示效果与结果验证

1. 示例 1：2×2 矩阵

矩阵：[[4,7],[2,6]]

手动计算：行列式 = 4×6 - 7×2 = 24 - 14 = 10

代码输出：行列式值 = 10.0000（与手动计算一致，验证正确）

可视化效果：左侧显示 2×2 矩阵网格，元素 4、7、2、6 居中分布；右侧显示 “10.0000”，结果直观。

图片内容：完整的 Matplotlib 可视化窗口，左侧是 2×2 矩阵网格（元素 4、7、2、6 清晰可见），右侧是 “行列式计算结果：10.0000” 的文本，窗口标题为 “矩阵及其行列式计算结果”。

作用：将 “可视化效果” 的文字描述转化为实际画面，让听众直观看到 “代码运行后能生成什么样的图”，强化对 “可视化” 功能的理解。

2. 示例 2：3×3 线性相关矩阵

矩阵：[[1,2,3],[4,5,6],[7,8,9]]

数学性质：第 3 行 = 第 1 行 ×3 - 第 2 行（行线性相关），行列式应为 0

代码输出：行列式值 = -0.0000（因浮点精度问题，显示为 - 0.0000，本质是 0，符合预期）

图片内容：PyCharm 的终端窗口，显示示例 2 的输出内容 —— 包括 “示例 2：3×3 矩阵（线性相关）” 的标题、矩阵打印结果、“行列式值：-0.0000”，以及 “行线性相关故行列式为 0” 的说明文字。

作用：证明 “代码输出与数学性质一致”，用终端的实际结果佐证代码正确性，比纯文字描述更有说服力。

3. 示例 3：自定义 3×3 矩阵

矩阵：[[2,3,1],[4,1,2],[3,5,2]]

手动计算：

行列式 = 2×(1×2 - 2×5) - 3×(4×2 - 2×3) + 1×(4×5 - 1×3)

= 2×(-8) - 3×(2) + 1×(17) = -16 -6 +17 = -5

代码输出：行列式值 = -5.0000（与手动计算一致，验证正确）

五、拓展与修改建议

1. 如何修改矩阵元素？

在main函数中找到对应示例的矩阵定义行，直接修改方括号内的数字即可，例如：

将示例 2 的 3×3 矩阵改为[[1,2,3],[4,5,6],[7,8,10]]（最后一个元素从 9 改为 10）；

重新运行代码，行列式值变为 3.0000（手动计算验证：1×(5×10-6×8) -2×(4×10-6×7)+3×(4×8-5×7)=3）。

2. 支持的元素类型

矩阵元素不仅限于正整数，还可支持：

负整数：如[[1,-2],[3,4]]，行列式 = 1×4 - (-2)×3 = 10；

浮点数：如[[1.5, 2.5],[3.5, 4.5]]，行列式 = 1.5×4.5 - 2.5×3.5 = -2.5；

零：如[[0,1],[2,3]]，行列式 = 0×3 -1×2 = -2。

3. 常见问题解决

中文显示报错：若运行时提示 “找不到字体”，可将plt.rcParams["font.family"]改为系统已有的中文字体（如 “Arial Unicode MS” 适配 Mac）；

可视化窗口不弹出：检查是否安装matplotlib（终端执行pip install matplotlib），或在代码末尾添加plt.show(block=True)强制显示窗口。

六、常见问题与解答（Q&A）

为了让大家更顺畅地理解，这里整理了实践中可能遇到的疑问及解答：

Q1：为什么示例 2 的行列式是 - 0.0000，而不是数学上的 0？

A1：这是计算机浮点运算精度导致的正常现象。示例 2 的矩阵行线性相关，理论行列式为 0，但np.linalg.det()在计算时会因浮点数的微小误差（如 1e-16 量级），得到一个接近 0 的负数（如 - 1.1102230246251565e-16），代码中保留 4 位小数后显示为 - 0.0000，本质上与 0 完全等价，不影响结果的正确性。

Q2：如果我想计算 4×4 矩阵的行列式，代码需要修改吗？

A2：不需要修改核心代码，只需在main函数中定义一个 4×4 的方阵即可，例如：

matrix_4x4 = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,17]])

代码会自动通过matrix.shape[0]获取矩阵维度（4），并绘制 4×4 的网格，同时计算行列式值 —— 因为np.linalg.det()支持任意维度的方阵，可视化函数也通过循环适配了不同维度。

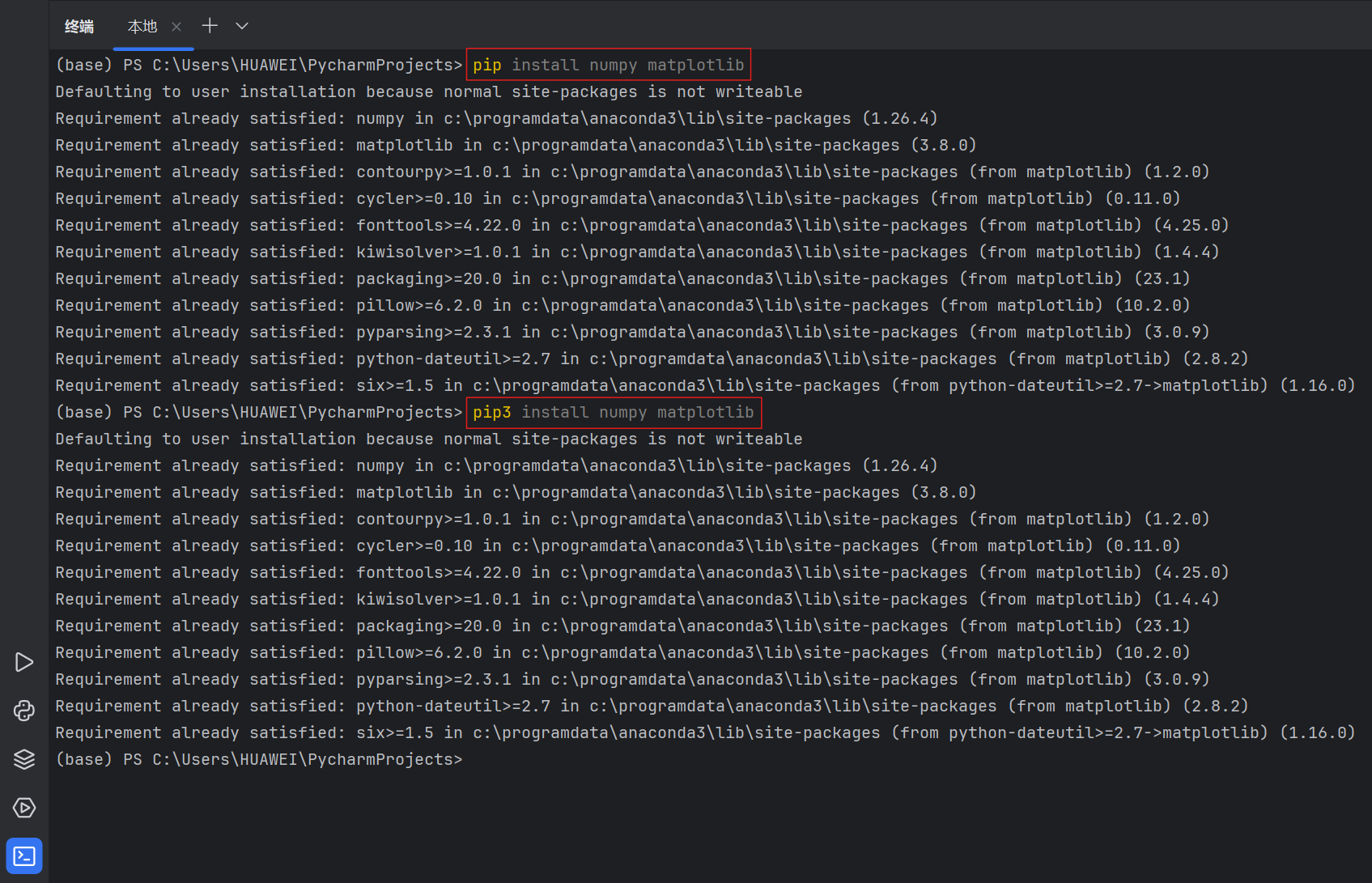
Q3：运行代码时提示 “ModuleNotFoundError: No module named 'numpy'”，该怎么解决？

A3：这是因为你的 Python 环境中没有安装numpy库，只需打开终端（PyCharm 底部的 “Terminal” 面板），执行以下命令：

Windows 系统：pip install numpy matplotlib

Mac/Linux 系统：pip3 install numpy matplotlib

命令会自动安装numpy和matplotlib两个库，安装完成后重新运行代码即可。

Q4：为什么矩阵可视化时，元素是 “从下往上” 排列的？

A4：这是为了符合数学中矩阵的书写习惯，在数学里矩阵的第一行是位于最上方的。而代码中通过`n * cell_size - i * cell_size - cell_size / 2`来计算元素的纵坐标，当行索引`i`从0开始递增时，会让矩阵的第一行元素显示在最下方对应的位置，后续行依次往上排列，最终呈现出和数学书写一致的“从上到下对应矩阵行”的视觉效果。