【算法基础课】笔记04——数学知识

最新推荐文章于 2024-06-15 16:17:24 发布

Avidorzzz

最新推荐文章于 2024-06-15 16:17:24 发布

阅读量2.2k

点赞数 1

文章标签：算法线性代数矩阵 c++

本文链接：https://blog.csdn.net/weixin_62340159/article/details/123028968

版权

数学知识

数论

建议学习的数学课程：线性代数、离散数学

1.质数
质数定理：1~n中有n/lnn个质数

质数的判定——试除法

O(sqrt(n))
约数成对（d<=n/d）

bool is_prime(int x){
	if(x<2)//0 1
		return false;
	for(int i=2;i<=x/i;i++)//优化
		if(x%i==0)//有因数
			return false;
	return true;
}

分解质因数——试除法

O(sqrt(n))
n中最多只包含一个大于sqrt(n)的质因子//反证法

void divide(int x){
	for(int i=2;i<=x;i++)
		if(x%i==0){
			int s=0;
			while(x%i==0)
				x/=i,s++;
			cout<<i<<' '<<s<<endl;
		}
	if(x>1)//超出自身
		cout<<x<<' '<<1<<endl;
	cout<<endl;
}

朴素筛法

挨个删倍数，剩余是质数

埃式筛法

只筛掉质数的倍数

线性筛法

常用
枚举质数
n只会被最小质因子筛掉,合数一定会被删

i % primes[j] == 0时，pj一定是i的最小质因子，pj一定是pj * i的最小质因子;
i % primes[j] != 0时,pj一定小于i的所有质因子,pj一定是pj * i的最小质因子.

int primes[N],cnt;
bool vis[N];

void get_primes(int n){
	for(int i=2;i<=n;i++){
		if(!vis[i])
			primes[cnt++]=i;
		for(int j=0;primes[j]<=n/i;j++){
			vis[primes[j]*i]=true;
			if(i%primes[j]==0)
				break;
		}
	}
}

2. 约数

试除法求所有约数

也是成对出现,枚举求

vector<int>get_divisors(int x){
	vector<int>res;
	for(int i=1;i<=x/i;i++)
		if(x%i==0){
			res.push_back(i);
			if(i!=x/i)
				res.push_back(x/i);
		}
	sort(res.begin(),res.end());
	return res;
}

约数个数及约数之和

步骤：

分解成因式相乘的形式（pi^ci）
参照下列公式求解

如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck

欧几里得算法

辗转相除

int gcd(int a,b){
	return b?gcd(b,a%b):a;
}

欧拉函数

ϕ(N)：1到n中与n互质的数的个数

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2rf2V2w3-1645329405274)(C:\Users\bingtongsuan\AppData\Roaming\Typora\typora-user-images\image-20220214121837276.png)]$

原理（容斥原理）：

1~N中去掉p1,p2,…,pk的所有倍数
加上所有pi * pj的倍数（把重复除去的补上）
减所有pi * pj * pk的倍数
以此类推，奇减偶加

步骤：
1.分解质因数
2.套公式

int phi(int x)
{
    int res = x;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
        {
            res = res / i * (i - 1);
            while (x % i == 0) x /= i;
        }
    if (x > 1) res = res / x * (x - 1);

    return res;
}

筛法求欧拉

线性筛法+欧拉

i % pj == 0时，ϕ(pj * i)=pj * ϕ(i)
i % pj !=0时，ϕ(pj * i)=(pj - 1) * ϕ(i)

int primes[N],phi[N],cnt;
bool vis[N];

void get_phi(int x) {
	phi[1] = 1;
	for (int i = 2; i <= n; i++) {
		if (!vis[i])
			primes[cnt++] = i, phi[i] = i - 1;
		for (int j = 0; primes[j]<= x / i; j++) {
			vis[i * primes[j]] = true;
			if (i % primes[j] == 0) {
				phi[primes[j] * i] = phi[i] * primes[j];
				break;
			}
			phi[primes[j] * i] = phi[i] * (primes[j] - 1);
		}
	}
	/*有求和需求就加上，记得变函数类型声明
	long long ans = 0;
	for (int i = 1; i <= n; i++)
		ans += phi[i];
	return ans;
	*/
}

欧拉定理

若a与n互质，则a^ϕ(n) ≡ 1(mod n)
推论（费马定理）：a^p-1≡1(mod p)
证明：a与每项相乘（两两不相同且互质的数只有ϕ(n)个——>乘积相等）

快速幂

快速求解 a^k mod p

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dkTv5pnU-1645329405275)(C:\Users\bingtongsuan\AppData\Roaming\Typora\typora-user-images\image-20220214152914216.png)]$

k拆成和（2的幂的形式），看二进制，上一个数平方mod p

先预处理出一张表，然后把幂用二进制表示，
有1的部分查表求值（挨个取出末位1）

在这里插入图片描述

int qmi(int a,int k,int p) {
	int ans = 1;
	while (k) {
		if (k & 1)//末位1取出
			ans = (long long)ans * a % p;
		k >>= 1;//次末位
		a = (long long)a * a % p;
	}
	return ans;
}

快速幂求逆元

p是质数时，除变乘

逆元：若整数 b，m 互质，并且对于任意的整数 a，如果满足 b|a，则存在一个整数 x，使得 a/b≡a×x(modm)，则称 x 为 b 的模 m 乘法逆元，记为 b−1(modm)。

b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时，bm−2 即为 b 的乘法逆元。

不互质就无解
特判p==2

扩展欧几里得

裴蜀定理:任意正整数a,b一定存在非零整数 x,y 使得 ax+by=(a,b)
$求 a i \times x i + b i \times y i = g c d (a i, b i) (a, b) = (b, a$
$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DgGGxbA4-1645329405278)(C:\Users\bingtongsuan\AppData\Roaming\Typora\typora-user-images\image-20220214162118275.png)]$

//记得引用x,y
int exgcd(int a, int b, int &x, int &y) {
	if (!b) {
		x = 1, y = 0;
		return a;
	}
	int d = exgcd(b, a % b, y, x);
	y -= a / b * x;
	return d;
}

$求解线性同余方程 a i \times x i \equiv b i (m o d m i) ：存在 y \in Z ，使得 a x = m y + b — — > a x + m y^{'} = b (y^{'} = y)$

中国剩余定理

给定两两互质的数，解线性同余方程组
有公式解：

在这里插入图片描述

高斯消元

解方程
高斯消元：线代行列变换——>系数矩阵（正）

初等行列变换：

把某一行乘一个非零的数
交换某两行
把某行的若干倍加到另一行去
经上述操作，最终解不变，方程组变为上三角形式。

解的可能性：（看三角形）

无解：零 = 非零
无穷解：零 = 零
唯一解：完美阶梯形

高斯消元法：
枚举每一列c（从第一列开始挨个往后看）“大顶10”

找绝对值最大的一行
将该行换到最上面
将该行第一个数变成1（同时除一个非零常数）
将下面所有行的第c列消成0（同时加减）
把处理完的那些列固定，重复执行1~5的操作
记得倒着把方程消一遍

简图：

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Xf8lxaW7-1645329405281)(C:\Users\bingtongsuan\AppData\Roaming\Typora\typora-user-images\image-20220215214843791.png)]$

实现过程中要小心的易错点：

eps 辅助浮点数判断，精度问题
记得 “ 倒消 ” ；
排除-0.00的状况
个人犯的sb错误：赋值写成相等orz

// a[N][N]是增广矩阵
int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )   // 找到绝对值最大的行
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;

        if (fabs(a[t][c]) < eps) continue;

        for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);      // 将绝对值最大的行换到最顶端
        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];      // 将当前行的首位变成1
        for (int i = r + 1; i < n; i ++ )       // 用当前行将下面所有的列消成0
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ;
    }

    if (r < n)
    {
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2; // 无解
        return 1; // 有无穷多组解
    }

    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[i][j] * a[j][n];

    return 0; // 有唯一解
}

高斯消元解异或方程

消成上三角矩阵 (枚举列,找非零行,交换,下面消零)
判断 (唯一/无/无穷解)

int gauss(){
	int r, c;
	for(r = c = 0; c < n; c ++){
		int t = r;//先找这一列
		for( int i = r; i < n; i ++)
			if(a[i][c]){
				t = i;
				break;
			}//找到
		if(!a[t][c])
			continue;//不存在
		
		for(int i = c; i <= n; i ++)
			swap(a[t][i], a[r][i]);
		
		for(int i = r + 1; i < n; i ++)
			if(a[i][c])
				for(int j = n; j >= c; j --)
					a[i][j] ^= a[r][j];
		r++;
	}

	if(r < n){
		for(int i = r; i < n; i ++){
			if(a[i][n])
				return -1;
		}
		return 1;
	}

	for(int i = n - 1; i >= 0; i --)
		for(int j = i + 1; j < n; j ++)
			a[i][n] ^= a[i][j] * a[j][n];
	
	return 0;
}

组合数学

递推法求组合数

1~2000
加法计数原理：

$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eDWY69LP-1645329731013)(C:\Users\bingtongsuan\AppData\Roaming\Typora\typora-user-images\image-20220216153117904.png)]$

// c[a][b] 表示从a个苹果中选b个的方案数
for (int i = 0; i < N; i ++ )
    for (int j = 0; j <= i; j ++ )
        if (!j) c[i][j] = 1;
        else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;

预处理逆元

1~1e5
快速幂 + 逆元 + 费马小定理
fact[i] = i ! mod (1e9 + 7)
infact[i] = (i!)^-1 mod (1e9 + 7)
所求即为：
$f a c t [a] * i n f a c t [b - a] * i n f a c t [b]$

首先预处理出所有阶乘取模的余数fact[N]，以及所有阶乘取模的逆元infact[N]
如果取模的数是质数，可以用费马小定理求逆元
int qmi(int a, int k, int p)    // 快速幂模板
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

// 预处理阶乘的余数和阶乘逆元的余数
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
    fact[i] = (LL)fact[i - 1] * i % mod;
    infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}

卢卡斯定理

记得long long
1~1e18
p进制转换
证明：https://www.cnblogs.com/onlyblues/p/15339937.html
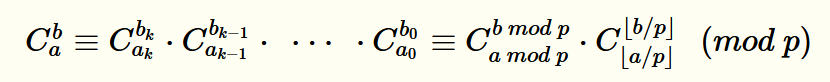
在这里插入图片描述

若p是质数，则对于任意整数 1 <= m <= n，有：
    C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)

int qmi(int a, int k, int p)  // 快速幂模板
{
    int res = 1 % p;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int C(int a, int b, int p)  // 通过定理求组合数C(a, b)
{
    if (a < b) return 0;//边界

    LL x = 1, y = 1;  // x是分子，y是分母
    for (int i = a, j = 1; j <= b; i --, j ++ )
    {//分子有b项
        x = (LL)x * i % p;
        y = (LL) y * j % p;
    }
    
    return x * (LL)qmi(y, p - 2, p) % p;
    /*
    ll res = 1;
	for(int i = 1, j = a; i <= b; i ++, j --){
		res = (ll)res * j % p;
		res = (ll)res * qmi(i, p - 2, p) % p;
	}
	return res;
    */

}

int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
//a%p后肯定是<p的,所以可以用C(),但a/p后不一定<p 所以用lucas继续递归
}

分解质因数法求组合数

Steps：

筛法求出范围内的所有质数
通过== C(a, b) = a! / b! / (a - b)!== 这个公式求出每个质因子的次数。 n! 中p的次数是== n / p + n / p^2 + n / p^3 + …==（p的倍数的个数 + p²的倍数 + …）
用高精度乘法将所有质因子相乘

Points：

分解质因数
高精乘
子p数 - 母p数

int primes[N], cnt;     // 存储所有质数
int sum[N];     // 存储每个质数的次数
bool st[N];     // 存储每个数是否已被筛掉


void get_primes(int n)      // 线性筛法求素数
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}


int get(int n, int p)       // 求n！中的次数
{
    int res = 0;
    while (n)
    {
        res += n / p;
        n /= p;
    }
    return res;
}


vector<int> mul(vector<int> a, int b)       // 高精度乘低精度模板
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size(); i ++ )
    {
        t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }

    while (t)
    {
        c.push_back(t % 10);
        t /= 10;
    }

    return c;
}

get_primes(a);  // 预处理范围内的所有质数

for (int i = 0; i < cnt; i ++ )     // 求每个质因数的次数
{
    int p = primes[i];
    sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}

vector<int> res;
res.push_back(1);

for (int i = 0; i < cnt; i ++ )     // 用高精度乘法将所有质因子相乘
    for (int j = 0; j < sum[i]; j ++ )
        res = mul(res, primes[i]);

卡特兰数

资料：https://oi-wiki.org/math/combinatorics/catalan/
序列——>路径
0：向右走一；1：向上走1

给定n个0和n个1，它们按照某种顺序排成长度为2n的序列，满足任意前缀中0的个数都不少于1的个数的序列的数量为：** Cat(n) = C(2n, n) / (n + 1)**

下图中，表示从 (0,0) 走到 (n,n) 的路径，在绿线及以下表示合法，若触碰红线即不合法。在这里插入图片描述（图源自AcWing)

由图可知，任何一条不合法的路径（如黑色路径），都对应一条从 (0,0) 走到 (n−1,n+1) 的一条路径（如灰色路径）。而任何一条 (0,0) 走到 (n−1,n+1) 的路径，也对应了一条从 (0,0) 走到 (n,n) 的不合法路径。

int n, a, b, res = 1;

int qmi(int a, int k, int p){
	int res = 1;
	while(k){
		if(k & 1)
			res = (ll)res * a % p;
		a = (ll)a * a % p;
		k >>= 1;
	}
	return res;
}

int main() {
	cin >> n;
	a = 2 * n, b = n;

	for(int i = a; i > a - b; i --)
		res = (ll)res * i % mod;
	for(int i = 1; i <= b; i ++)
		res = (ll)res * qmi(i, mod - 2, mod) % mod;

	res = (ll)res * qmi(n + 1, mod - 2, mod) % mod;

	cout << res << endl;
	
	return 0;
}

容斥原理

拓展：https://oi-wiki.org/math/combinatorics/inclusion-exclusion-principle/
韦恩图：相交圆
简述：1 - 2 + 3 - 4 + … +(-1)^n-1n（算元素个数，数字代表集合）

抽象出一个韦恩图，表示Si（按性质划分）
$eg. S_2=\{2,4,6,8,10\}，S_3=\{3,6,9\}，\\则答案为|S_3| + |S_2| - |S_2 ∩ S_3|\\ 求|S_p|：1~n中p的倍数的个数，即[n/p]\\ 求|S_{p1} ∩ S_{p2} ∩...∩ S_{pk}|，即[n/p_1 p_2...p_k]$
位运算：看位上的数（1表示被选，0没被选）i >>k &1
集合选取个数与符号关系：奇正偶负

for(int i = 1; i < 1 << m; i ++ ){
	int t = 1, cnt = 0;
	for(int j = 0; j < m; j ++){
		if(i >> j & 1){
			cnt++;
			if((ll)t * a[j] > n){
				t = -1;
				break;
			}
			t *= a[j];
		}
	}

	if(t != -1){
		if(cnt % 2)
			ans += n / t;
		else
			ans -= n / t;
	}
}

简单博弈论

NIM游戏

制胜：当使得两堆石子数量一样之后，后续只需进行镜像操作
必胜态（使得后手为必败态）
必败态（走不到任何一个必败状态）

具体操作：异或

a_1 ^ a_2 ^ … ^ a_n == 0 则先手必败
！= 0 则先手必胜

a_1 ^ a_2 ^ … ^ a_n = x != 0
x的二进制表示中最高一位1在第k位，a1~an中必然存在一个数ai，ai的第k位是1

证明：

0 ^ 0 ^ … ^ 0 = 0
当前不是0，后续必定变成0
（关键步骤转化）
当前是0，后续非0
（反证法：会推出什么都不拿的状态）

分析猛如虎，代码贼简单

while(n --){
	cin>> x;
	ans ^= x;
}
if(ans)
	cout<<"Yes";
else
	cout<< "No";

台阶NIM游戏

只看奇数级台阶上的石子
a1 ^ a3 ^ … ^ an != 0 则先手必胜

拆分 - Nim游戏

把石子堆转化为有向图,求SG 然后Mex

Mex运算

求出不属于集合S的最小非负整数的运算
mex(S) = min{x}, x属于自然数，且x不属于S

SG函数

记忆化搜索求
更新局面，终点SG值定义为0
起点代表整体：整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即SG(G) = SG(s)。
SG(x)为x的后继节点y1, y2, …, yk
SG(x) = mex({SG(y1), SG(y2), …, SG(yk)})

有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0。
有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。
（原因：见NIM游戏，非０变０，０变非０）

公平组合游戏ICG

由两名玩家交替行动；
在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关；
不能行动的玩家判负；

有向图游戏

SG(G) = SG(G1) ^ SG(G2) ^ … ^ SG(Gm)

集合—Nim游戏
转化成有向图求SEG（哈希+记搜+NIM）

int sg(int x){
	if(f[x] != -1)
		return f[x];

	unordered_set<int> S;//哈希

	for(int i = 0; i < m; i ++){
		int sum = s[i];
		if(x >= sum)
			S.insert(sg(x - sum));
	}

	for(int i = 0; ; i ++)
		if(!S.count(i))
			return f[x] = i;
}//记忆化搜索

Avidorzzz

关注

1
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
【算法基础课】笔记04——数学知识

数学知识数论建议学习的数学课程：线性代数、离散数学1.质数质数定理：1~n中有n/lnn个质数质数的判定——试除法O(sqrt(n))约数成对（d<=n/d）bool is_prime(int x){ if(x<2)//0 1 return false; for(int i=2;i<=x/i;i++)//优化 if(x%i==0)//有因数 return false; return true;}分解质因数——试除法O(sqrt(n))n中最多只
复制链接

扫一扫