量子力学概论第一章---波函数

首先上来就是一个薛定谔方程：

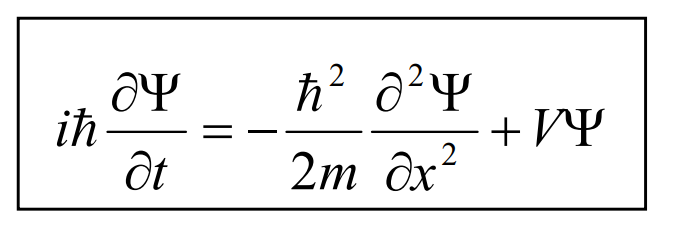
描述的是微观粒子的波函数与势函数的关系，为啥要搞这么一个方程捏？因为大佬们想知道微观粒子的运动状态，如果我们知道空间范围的势函数V，通过解微分方程就可以知道粒子的波函数啦。波函数又是啥？就是粒子在空间的位置与时间的函数，波函数的值是一个概率，t时刻，粒子处于x位置的概率。既然是概率，那任意时刻t，粒子在a，b范围内的概率：

然后插一段有趣的讨论：波函数其实描述的是不确定的粒子状态，那假如我们通过仪器测量粒子的位置，并发现就在位置C处，那测量之前它应该在哪里呢？有三种回答:

现实主义派就说了，粒子还是在C处。这就有bug了呀，你说在C，但是波函数却不能确定粒子的位置。

正统学派：粒子哪也不在。唯物主义的人是不是有点难以接受了，他们的观点是测量强迫粒子出现，有人甚至说测量不仅扰动了观测量还产生了它......大部分物理学家接受这个观点的。

不可知论学派：什么问题？我们拒绝回答。测量前在哪？要知道在哪就得测量，你没测量怎么知道，你们搁这讨论不就是故弄玄虚嘛。

三种观点哪个是正确的呢？1964年，John Bell宣布：粒子在测量前有没有一个确定的位置在观测上会导致不同的测量结果。（真理掌握在大部分物理学家手上啊）

刚刚讨论的是测量前粒子应该在哪，现在讨论第一次测完再测第二次，粒子应该在哪。这一次就没有啥分歧了，粒子就在C。为啥捏，因为第一次测量使波函数坍塌。

坍塌前后的波函数变化

这个讨论就先结束了

回到前面波函数，一个概率函数一定具备一个特点：概率之和为1。所以波函数需要归一化成下面这个形式：

我们知道波函数是一个随时间变化的函数，就是说每个时刻波函数都得是归一的，时间又是连续的，这咋搞？很神奇，我们首先将t=0时刻的波函数归一化，然后，它会自动保持归一化！证明如下（知道结论就行）：求粒子概率和关于时间的导数，然后发现不随时间改变，就是说位置概率的总和是一个常数，而t=0时刻归一化了。

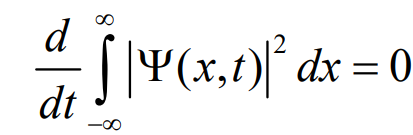
然后类似经典力学里面，描述物体一般有位置，速度，动量，能量等特征，这里也是，前面波函数不是可以求出粒子的位置概率嘛，那t时刻粒子位置的期待值（平均）：

那粒子的运动速度不就是位置关于时间的导数了：

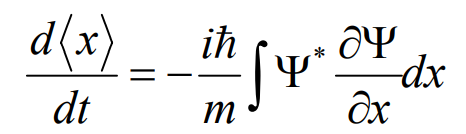
是不是有一点草率，位置都不确定，速度就这样算出来了，是这么一回事吧，反正我就假设速度的期待值就等于位置期待值关于时间的导数了。

但是我们更感兴趣的是粒子的动量：

这里引入一个算符概念：

中间就是表示算符用（）括起来，比如（x）就表示这是一个位置。

粒子的动能：

哇前面讲了很多波函数的妙用，但是我们知道的波函数就是一个概率，这些期待值可信吗？是的，这里就有一个不确定原理：

这里的意思就是当粒子的位置越准确，那它的动量就越不准确。

就像这两个波，第一个波的位置一直晃，我们很难描述粒子的位置，但是波长很清晰，根据德布罗意关系，粒子的动量就很明确了。

第二个波，我们几乎很确定粒子的位置，但是波长，似乎都定义不了波长，因此动量也不确定。

第一章内容结束！