层次分析法(AHP)详细原理及改进+MATLAB代码

Lyihp

已于 2023-11-30 14:09:24 修改

阅读量9.1k

点赞数 39

分类专栏： matlab 数学建模文章标签： matlab 算法数学建模

于 2023-11-16 11:55:41 首次发布

本文链接：https://blog.csdn.net/weixin_62616638/article/details/134435224

版权

matlab 同时被 2 个专栏收录

2 篇文章 0 订阅

订阅专栏

数学建模

2 篇文章 0 订阅

订阅专栏

1. 什么是层次分析法

2. 层次分析法的基本步骤

2.1 建立层次结构模型

2.2 构造判断矩阵(也叫成对比较矩阵/互反矩阵)

1. 什么是层次分析法

❑ 层次分析法（The analytic hierarchy process）简称AHP，在20世纪70年代初期由美国匹兹堡大学运筹学家托马斯·塞蒂（T.L. Saaty）在为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”的课题时提出。它是一种应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。

❑ 层次分析法是对一些较为复杂、较为模糊的问题做出决策的简易方法，它特别适用于那些难于完全定量分析的问题。

❑ 层次分析法根据问题的性质和要达到的总目标，将问题分解为不同的组成因素，并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型，从而最终使问题归结为最低层（供决策的方案、措施等）相对于最高层（总目标）的相对重要权值的确定或相对优劣次序的排定。

2. 层次分析法的基本步骤

2.1 建立层次结构模型

❑ 将决策的目标、考虑的因素(决策准则)和决策方案，按它们之间的相互关系分为目标层、准则层和方案层，绘出层次结构图。

目标层：决策的目的、要解决的问题。
准则层：考虑的因素、决策的准则。
方案层：决策时的备选方案。

2.2 构造判断矩阵(也叫成对比较矩阵/互反矩阵)

❑ 从层次结构模型的第2层开始，对于从属于(或影响)上一层每个因素的同一层诸因素，构造判断矩阵，直到最下层。

❑ 在确定各层次各因素之间的权重时，如果只是定性的结果，则常常不容易被别人接受，因而Saaty等人提出：一致矩阵法，即

不把所有因素放在一起比较，而是两两相互比较。
采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。

❑ 判断矩阵是表示本层所有因素针对上一层某一个因素的相对重要性的比较。判断矩阵的元素用Saaty的1-9标度方法给出。（心理学家认为成对比较的因素不宜超过9个，即每层不要超过9个因素。）

即：

2.3 层次单排序及其一致性检验

单次总排序

❑ 层次单排序是指针对上一层某元素将本层中所有元素两两评比，并开展层次排序，进行重要顺序的排列，具体计算可依据判断矩阵 A 进行，计算中确保其能够符合AW=𝜆𝑚𝑎𝑥𝑊的特征根和特征向量条件。在此，A 的最大特征根为λmax，对应λmax的正规化的特征向量为W，𝑤𝑖为 W 的分量，其指的是权值，与其相应元素单排序对应。

❑ 权重向量（W）与最大特征（λmax）的计算可以用和积法或方根法。

和积法计算最大特征根

计算步骤：

matlab代码实现：

%% 利用【和积法】求最大特征根及对应的特征向量
clc;clear;
B = [1,1/5,1/3; 5,1,3; 3,1/3,1]; %判断矩阵
B1 = B./repmat(sum(B),3,1); %列正规化 %将判断矩阵按行扩大3倍，按列扩大1倍
W0 = sum(B1,2); %列正规化后行相加
W = W0/sum(W0); %W0正规化后即为所求的特征向量
BW = B*W;
lada_max = sum(BW./W)/3; %最大特征值
disp(['和积法求得的最大特征值：',num2str(lada_max)]);
disp('和积法求得的最大特征值对应的特征向量：');
disp(W);

方根法计算最大特征根

计算步骤：

matlab代码实现：

%% 利用【方根法】求最大特征根及对应的特征向量
clear;
B = [1,1/5,1/3; 5,1,3; 3,1/3,1]; %判断矩阵
B1 = prod(B,2).^(1/3); %判断矩阵按行相乘，所得乘积分别开n方
W = B1./sum(B1);
lada_max = sum(B*W./W)/3;
disp(['方根法求得的最大特征值：',num2str(lada_max)]);
disp('方根法求得的最大特征值对应的特征向量：');
disp(W);

用matlab自带的函数计算最大特征根

%% 直接利用matlab自带的函数求解
clear;
B = [1,1/5,1/3; 5,1,3; 3,1/3,1]; %判断矩阵
[x,y] = eig(B); %求矩阵的特征值和特征向量，x为特征向量矩阵，y为特征值矩阵。
eigenvalue = diag(y); %求对角线向量
lamda_max = max(eigenvalue); %求最大特征值
for i=1:length(B) %求最大特征值对应的序数
    if lamda_max==eigenvalue(i)
        break;
    end
end
y_lamda = x(:,i); %求矩阵最大特征值对应的特征向量
disp(['MATLAB函数求得的最大特征值：',num2str(lamda_max)]);
disp('MATLAB函数求得的最大特征值对应的特征向量：');
disp(y_lamda);

三种方法计算结果比较：

一致性检验

❑ 用一致性指标 CI 来检验判断的一致性指标（Consistency Index）：

其中λmax为最大特征根，n为矩阵的阶数。
CI=0表示判断矩阵完全一致，此时λmax=n。CI越大，判断矩阵的不一致性程度越严重，此时λmax>n。

❑ 然后根据一致性指标 CI 、平均随机一致性指标 RI 求解一致性比例 CR ：

其中Satty模拟1000次得到的随机一致性指标 RI 取值表如下：

如果CR<0.1，则认为判断矩阵的一致性可以接受，否则需要对判断矩阵进行适当的修改。

❑ 注意：方案层和准则层的权重确定都需要用到层次单排序！

2.4 层次总排序及其一致性检验

层次总排序

计算某一层次所有因素对于最高层（目标层）相对重要性的权值，称为层次总排序。该过程是从最高层次向最低层次依次进行：

一致性检验

3. 层次分析法的改进

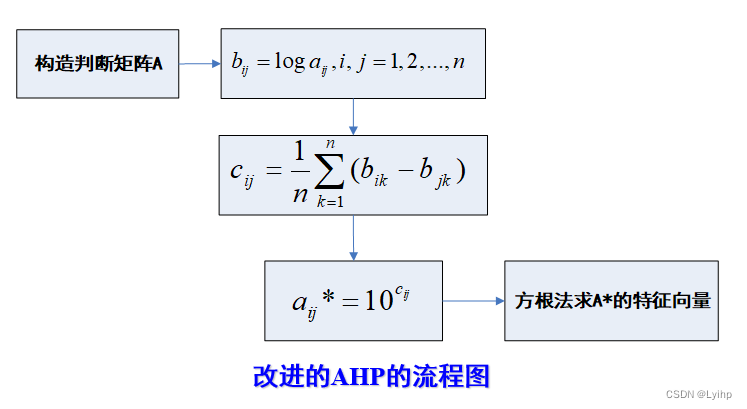
利用最优传递矩阵的概念，提出一种改进的层次分析法。该方法得到的判断矩阵可以一次得到权重值，不需要进行一致性检验，从而避免调整判断矩阵的盲目性。

设A=［ $a_{ij}$ ］、B=［ $b_{ij}$ ］、C=［ $c_{ij}$ ］∈Rn×n

定义1 若 $a_{ij}=1/a_{ji}$ ，则称A为互反矩阵,

若 $b_{ij}=-b_{ji}$ ，则称B为反对称矩阵。

定义2 A是互反矩阵，若 $a_{ij}=a_{ik}\cdot a_{kj}$ ，则称A是一致的；

若B是反对称阵，且 $b_{ij}=b_{ik}+b_{kj}$ ，则称B是传递的。

若A是一致阵，则B = lgA ( $b_{ij}= lga_{ij}$ ,任意i、j)是传递的；
若B是传递阵，则A = 10B ( $a_{ij}=10^{b_{ij}}$ , 任意i、j)是一致的。

定义3 若存在传递矩阵C，且使 $\sum_{i=1}^{n}\sum_{j=1}^{n}(c_{ij}-b_{ij})^{2}$ 最小，则称C为B的最优传递阵。

显然若A是互反矩阵，B = lgA，C是B的最优传递阵，那么 $A* = 10^{c}$ 可以认为是A的一个拟优一致阵，它满足使 $\sum_{i=1}^{n}\sum_{j=1}^{n}(lga_{ij}^{*}-a_{ij})^{2}$ 最小，而非 $\sum_{i=1}^{n}\sum_{j=1}^{n}(a_{ij}^{*}-a_{ij})^{2}$ 最小。

定理1 若B是反对称阵，则B的最优传递阵C满足

总之：

4. 层次分析法的Matlab代码

用一个函数封装，函数的输入为判断矩阵A，输出有一致性指标CI，随机一致性指标RI，一致性比例CR和求得的权重Q。

%%AHP函数
function [CI,RI,CR,Q] = AHPFuc(A)
[n,m]=size(A); %获取指标个数
%判断是否是互反矩阵
for i=1:n
    for j=1:m
        if A(i,j)*A(j,i)==1   %或A(i,j)*A(j,i)<=1.001 && A(i,j)*A(j,i)>=0.999
        else
            disp('判断矩阵不是互反矩阵，输入有误，请重新输入');
        end
    end
end
%求特征值特征向量,找到最大特征值对应的特征向量
[V,D]=eig(A);    %D是特征值，V是特征向量
[tzz,pos]=max(max(D));     %找到最大的特征值及其对应的列
tzx=V(:,pos); %最大特征值对应的特征向量
%% 一致性检验
CI=(tzz-n)/(n-1);
RI_R=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59];
%判断是否通过一致性检验
Q=-1; %如果没有通过一致性检验返回-1
RI=RI_R(1,n);
CR=CI/RI;
if CR>=0.1
   fprintf('没有通过一致性检验，需要对判断矩阵重新构造\n');
else
   % disp(['CI=',num2str(CI)]);
   % disp(['CR=',num2str(CR)]);
   fprintf('通过一致性检验\n');
   for i=1:n
       Q=tzx./sum(tzx);
   end
   % disp(Q);
end
end

%% AHP改进 -- 使用函数，并且判断矩阵不一致时用改进法重新调整
clc;clear;
%% 输入判别矩阵
%不一致矩阵
A = [1 5 3 3
    1/5 1 1/3 3
    1/3 3 1 5
    1/3 1/3 1/5 1];
%一致矩阵
% A = [1 5 3 7
%     1/5 1 1/3 3
%     1/3 3 1 5
%     1/7 1/3 1/5 1];
[n,m] = size(A);
[CI,RI,CR,Q] = AHPFuc(A);
%%
if Q==-1
    B = log10(A);
    C = zeros(n,m);
    for ii=1:n
        for jj=1:m
            C(ii,jj) = sum(B(ii,:)-B(jj,:))/n;
        end
    end
    A2 = 10.^C;
    [CI2,RI2,CR2,Q2] = AHPFuc(A2);
    disp(Q2);
end

Lyihp

关注

39
点赞
踩
119

收藏

觉得还不错? 一键收藏
1
评论
层次分析法(AHP)详细原理及改进+MATLAB代码

❑ 层次分析法（The analytic hierarchy process）简称AHP，在20世纪70年代初期由美国匹兹堡大学运筹学家托马斯·塞蒂（T.L. Saaty）在为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”的课题时提出。它是一种应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。❑ 层次分析法是对一些较为复杂、较为模糊的问题做出决策的简易方法，它特别适用于那些难于完全定量分析的问题。❑ 层次分析法根据问题的性质和要达到的总目标，将问题分解为不同的组成因
复制链接

扫一扫