一阶导数
导数最大的作用是判断复杂函数的单调性,则可用一阶导判断原函数的单调性。
一阶导数>0:函数单调递增;
一阶导数<0:函数单调递减;
一阶导数=0:函数是常函数。
也可以通过一阶导数=0的根来判断出函数的单调区间,进而知道函数的趋势图像。而当一阶导数
无法判断函数的单调性时,需要二阶求导。
二阶导数
二阶导数可判断原函数的凹凸性。
二阶导数>0:一阶导数是单调增函数,即原函数在各店的切线斜率随x的增大而增大的,原函数是凹图像。
二阶导数<0:一阶导数是单调减函数,即原函数在各店的切线斜率随x的增大而减小的,原函数是凸图像。
考研大纲规定:
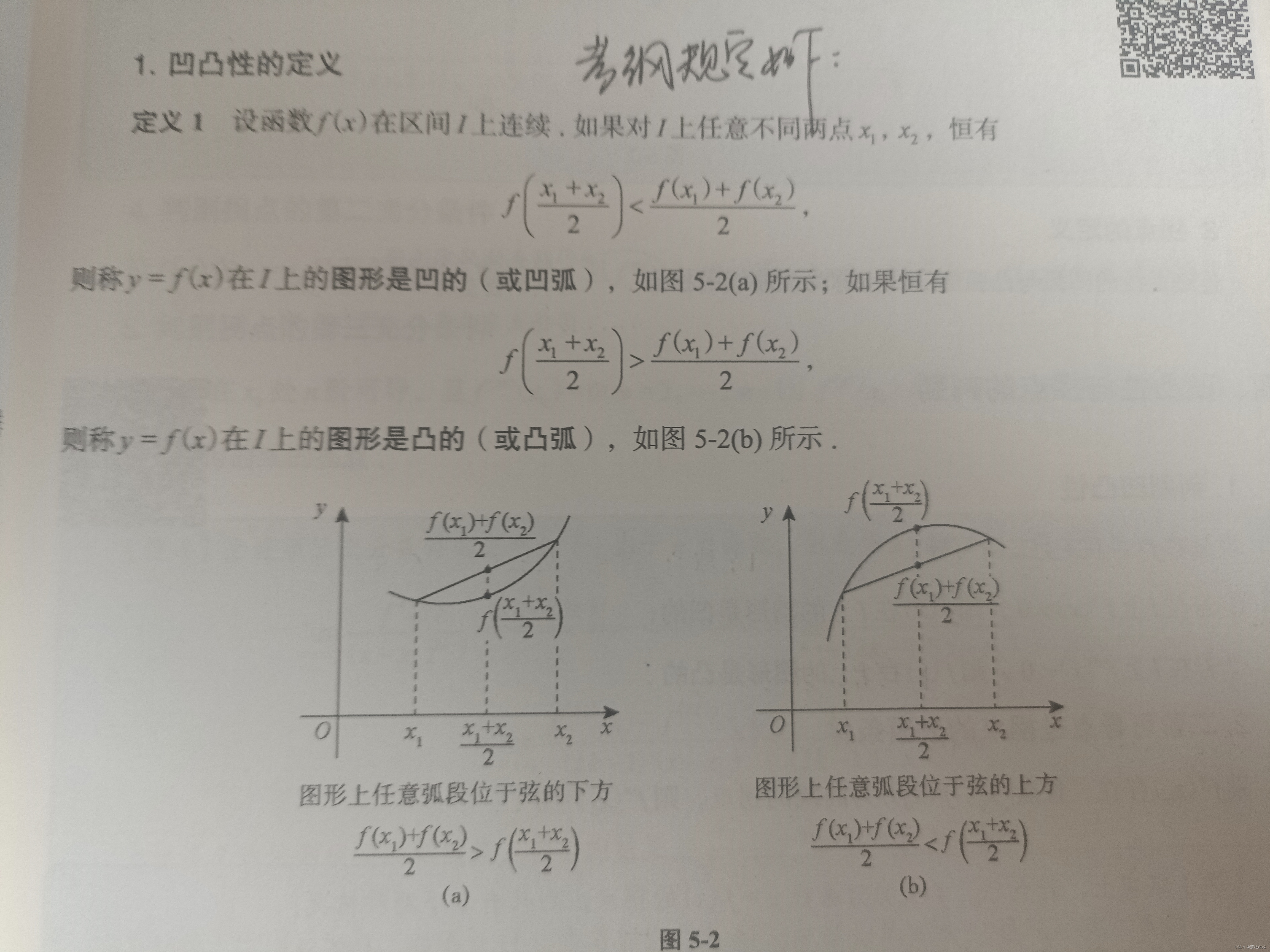









 本文介绍了如何利用一阶导数判断函数的单调性,包括递增、递减和常函数,以及通过一阶导数等于0的根确定单调区间。同时,详细解释了二阶导数的作用,即判断函数的凹凸性。提及考研大纲对这些内容的要求。
本文介绍了如何利用一阶导数判断函数的单调性,包括递增、递减和常函数,以及通过一阶导数等于0的根确定单调区间。同时,详细解释了二阶导数的作用,即判断函数的凹凸性。提及考研大纲对这些内容的要求。
















 8988
8988

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








