矩阵分解及其Python代码实现

有如下R(5,4)的打分矩阵：（“-”表示用户没有打分）

其中打分矩阵R(n,m)是n行和m列，n表示user个数，m行表示item个数

那么，如何根据目前的矩阵R（5,4）如何对未打分的商品进行评分的预测（如何得到分值为0的用户的打分值）？

可以利用矩阵分解解决这个问题。

矩阵R可以近似表示为P与Q的乘积：R（n,m）≈ P(n,K)*Q(K,m)

将原始的评分矩阵分解成两个矩阵和的乘积：

 矩阵P(n,K)表示n个user和K个特征之间的关系矩阵，这K个特征是一个中间变量，矩阵Q(K,m)的转置是矩阵Q(m,K)，矩阵Q(m,K)表示m个item和K个特征之间的关系矩阵，这里的K值是自己控制的，可以使用交叉验证的方法获得最佳的K值。为了得到近似的R(n,m)，必须求出矩阵P和Q。

求矩阵P和Q:

1.令算法给出的预测值为,则

（利用矩阵乘法）

矩阵乘法：

有两个矩阵A和B

A矩阵和B矩阵可以做乘法运算必须满足A矩阵的列的数量等于B矩阵的行的数量

运算规则：A的每一行中的数字对应乘以B的每一列的数字把结果相加起来

结果：行数量为A的行数量，列数量为B的列数量

 

2.损失函数（loss function）

损失函数是用来度量模型的预测值和真实值的差异程度的运算函数

最小二乘法：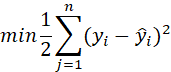

极大似然估计（根据现实世界的事件发生频率来反推出发生这些事件最可能的概率模型是什么样子，似然是该模型是真实模型的可能性）

交叉熵

使用原始的评分矩阵与重新构建的评分矩阵之间的误差的平方作为损失函数，即：如果R(i,j)已知，则R(i,j)的误差平方和为：

最终，需要求解所有的非“-”项的损失之和的最小值：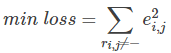

(目的就是最小化损失函数） 

3.使用梯度下降法获得p和q的分量：

梯度下降法：

 梯度的负方向是损失函数下降最快的方向

（1）求解损失函数的负梯度：

（求偏导）

偏导数：

在数学中，一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定（相对于全导数，在其中所有变量都允许变化）

多元：自变量不止一个

核心：求谁的偏导数，其它自变量均视为常数。

偏导数的定义计算：分段函数，在分段点上必用定义求偏导

高阶偏导数（对偏导数再求偏导）：先从低阶开始求

高阶混合偏导数相等条件：混合偏导数若均为连续函数，则必相等

（2）根据负梯度的方向更新变量：

 （其中ɑ为步长）

4. 不停迭代直到算法最终收敛（直到sum(e^2) <=阈值（临界值）

迭代法也称辗转法，是一种不断用变量的就职递推新值的过程。迭代是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次迭代，每一次迭代得到的结果会作为下一次迭代的初始值。

（为了防止过拟合，增加正则化项）

5.增加正则化项

正则化（也可以称为平滑项）是为了解决过拟合问题

平滑项可以使得训练的函数对输入不是很敏感。

如果输入数据有一定噪声的话，一个平滑的函数受到的影响会很小。反之，如果训练出的函数不平滑的话，对有噪声的数据进行预测将会有不好的结果。

（过拟合：模型过于复杂，在训练集上面的拟合效果非常好，甚至可以达到损失为0，但在测试集的拟合效果很不好）

（欠拟合：模型过于简单，在训练集和测试集的拟合效果都不好）

采用正则化方法会自动削弱不重要的特征变量，自动从许多的特征变量中“提取”重要的特征变量，减小特征变量的数量级。

1. 防止过拟合
2. 正则化项的引入其实是利用了先验知识，体现了人对问题的解的认识程度或者对解的估计。
3. 有助于处理条件数不好的情况下矩阵求逆很困难的问题。

 即：

3.使用梯度下降法获得修正的p和q分量： 

（1）求损失函数的负梯度：

（2）根据负梯度的方向更新变量：

 

 4. 不停迭代直到算法最终收敛（直到sum(e^2) <=阈值）

【预测】利用上述的过程，我们可以得到矩阵和，这样便可以为用户 i 对商品  j 进行打分：

                 

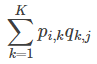
代码实现：

import matplotlib.pyplot as plt
from math import pow
import numpy
def matrix_factorization(R,P,Q,K,steps=5000,alpha=0.0002,beta=0.02):
    Q=Q.T #.T操作表示矩阵的转置
    result=[]
    for step in range(steps):
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j]>0:
                    eij=R[i][j]-numpy.dot(P[i,:],Q[:,j])#.dot(P,Q)表示矩阵内积
                    for k in range(K):
                        P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])
                        Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])
        eR=numpy.dot(P,Q)
        e=0
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j]>0:
                    e=e+pow(R[i][j]-numpy.dot(P[i,:],Q[:,j]),2)
                    for k in range(K):
                        e= e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))
        result.append(e)
        if e<0.001:
            break
    return P,Q.T,result


if __name__ == '__main__':
    R=[
        [5,3,0,1],
        [4,0,0,1],
        [1,1,0,5],
        [1,0,0,4],
        [0,1,5,4]
    ]
    R=numpy.array(R)
    N=len(R)
    M=len(R[0])
    K=2
    P=numpy.random.rand(N,K)#随机生成一个N行K列的矩阵
    Q=numpy.random.rand(M,K)#随机生成一个M行K列的矩阵
    nP,nQ,result=matrix_factorization(R,P,Q,K)
    print("原始的评分矩阵R为：\n",R)
    R_MF=numpy.dot(nP,nQ.T)
    print("经过MF算法填充0处评分值后的评分矩阵R_MF为：\n",R_MF)
    #损失函数的收敛曲线图
    n=len(result)
    x=range(n)
    plt.plot(x,result,color='r',linewidth=3)
    plt.title("Convergence curve")
    plt.xlabel("generation")
    plt.ylabel("loss")
    plt.show()

运行结果：